牛牛的函数

今天学习了两个知识：

费马小定理：

若p为一个质数，整数a不是p的倍数，那么a^（p-1）mod p=1。

令a=n-1，同时两边同除n-1则

 ${(n-1)}^{mod-2}%{mod}=\frac{1}{n-1} $
对于

 $f(n)=n^a+n^{a+1}+...+n^{b-1}+n^b=\frac{x^a*(1-n^{b-a+1})}{1-n}$
可以转换为

$f(n)=(n^{(b+1)}-n^{a})*(n-1)^{mod-2}%{mod}$

 

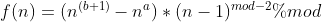
 接着就可以利用快速幂和快速乘分别计算