pta L2-004 这是二叉搜索树吗
题目链接:https://pintia.cn/problem-sets/994805046380707840/problems/994805070971912192
评价:应用很灵活,难点在于怎么处理镜像,在根本上还是考了二叉搜索树的性质;
题目思路:
题目可以这么做,我们拿到第一个样例分析,
7
8 6 5 7 10 8 11
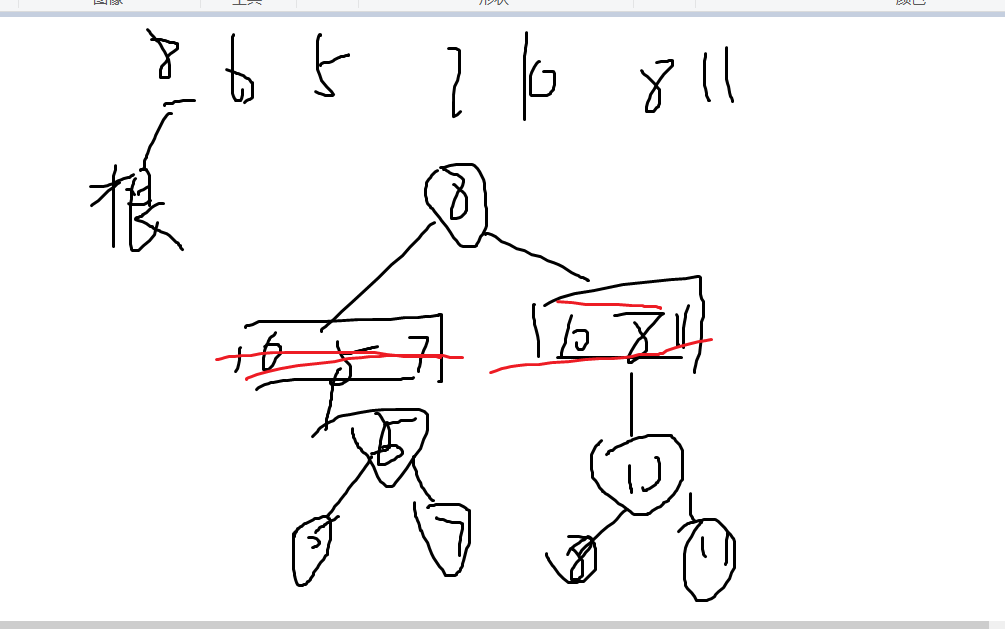
这很典型,根节点的键值大于左子树的键值,同时小于右子树的键值;
我们就可以这样分析了,从根节点的下一个节点出发,挨个遍历,一直找到比根节点的键值的大的节点,就停止了,同时,这也确定了左子树的范围;
另外,从右边界出发,向root位置靠拢,一直找到比根节点键值小的节点,就确定了右子树的范围,
那镜像呢?
镜像则是反过来处理,左边界是找比根节点键值小的节点,右边界同理;
另外在开始的时候判断root的位置和right的位置是否合法,在判断遍历完以后左边界的右边在减去1是否等于右边界的左边
然后在从检查从根的下一个带左边界的右边,右边界的左边到右边;
最后把根节点每次都压入last数组,表示每次压入的都是根节点,就确定了后序序列;
同时
在主函数中判断last的个数是不是等于n,如果等于n就证明是BST,因为节点全被压进去了;
不是就证明在check中出现了不合法性,就不是bst了
那说了这么多,镜像究竟是怎么处理的呢?
我们引入一个bool判断,如果这个last个数不等于n就不是bst
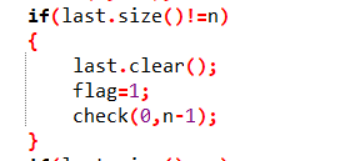
我们先清last数组为0,然后置bool变量为true(开始的时候是false),然后对应check函数中的对于镜像的遍历;
在判断last的长度,如果是,就正常输出了,如果不是,输出no就ok啦

Talk is cheap. Show me the code.
1 #include<bits/stdc++.h> 2 using namespace std; 3 int n; 4 bool flag; 5 vector<int>a,last; 6 void check(int root,int right) 7 { 8 if(root>right)//判断合法性 9 return ; 10 int i=root+1;//从下一个开始,因为根节点已被确定 11 int j=right;//边界 12 if(!flag)//非镜像 13 { 14 while(i<=right&&a[root]>a[i]) 15 i++; 16 while(j>root&&a[j]>=a[root])//题目说右子树小于等于 17 j--; 18 } 19 else//镜像 20 { 21 while(i<=right&&a[root]<=a[i])//置左右子树相反 22 i++; 23 while(j>root&&a[j]<a[root]) 24 j--; 25 } 26 if(i-1!=j) 27 return ;//合法性 28 check(root+1,j);//j其实就是右子树的左边界,在这范围内也就是遍历左子树 29 check(i,right);//同理 30 last.push_back(a[root]);//有后序遍历的味道了 31 } 32 int main() 33 { 34 cin>>n; 35 for(register int i=0;i<n;i++) 36 { 37 int x; 38 cin>>x; 39 a.push_back(x);//先序序列 40 } 41 check(0,n-1);//从root到right的检查 42 if(last.size()!=n)//如果是镜像 43 { 44 last.clear(); 45 flag=1;//置为镜像,对应check中的检查方式 46 check(0,n-1); 47 } 48 if(last.size()==n)//是的话就说明是BST 49 { 50 printf("YES\n"); 51 for(register int i=0;i<n;i++) 52 { 53 printf("%d",last[i]); 54 if(i<n-1) 55 printf(" "); 56 } 57 } 58 else 59 cout<<"NO"; 60 return 0; 61 }
i,j的位置如图所示
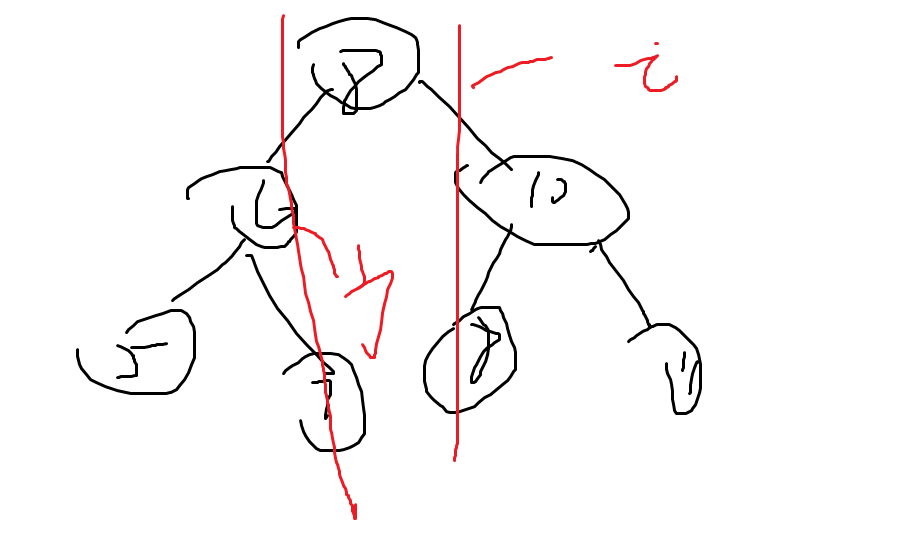
本文来自博客园,作者:江上舟摇,转载请注明原文链接:https://www.cnblogs.com/LQS-blog/p/16170777.html




 浙公网安备 33010602011771号
浙公网安备 33010602011771号