Deep Reinforcement Learning
Deep Reinforcement Learning
基础知识
强化学习基本概念
-
强化学习主体被称为智能体(Agent);
环境(environment)是智能体交互的对象;
环境中有一个状态(state),是对当前时刻环境的概括;
状态空间\(\mathcal{S}\)(state space)是值所有可能存在状态的集合;
动作(action)是智能体基于当前状态所做的决策;
动作空间\(\mathcal{A}\)是指所有可能动作的集合;
奖励(reward)是指智能体执行一个动作之后环境返回智能体的数值;
状态转移(state transition)是指智能体从当前时刻的状态转移到下一个时刻的状态的过程;
策略(policy)是根据观测到的状态如何做出决策,即如何从动作空间中选取一个动作;
智能体与环境交互是指智能体观测到的环境的状态s做出动作a,动作会改变环境的状态,环境反馈给智能体奖励r以及新的状态s'。 -
状态转移可能是随机的,例如超级玛丽,用状态转移概率函数来描述状态转移,\(p_t(s' \mid s, a) = \mathbb{P}(S_{t+1} = s' \mid S_t = s, A_t = a)\),表示在当前状态s,智能体执行动作a,环境状态变成s'。
-
强化学习的目标是得到一个策略函数,在每个时刻根据观测到的状态做出决策,可以有随机策略和确定策略:
- 随机策略可以用一个概率密度函数表示:\(\pi(a \mid s) = \mathbb{P}(A = a \mid S = s)\),该策略函数的输出为[0, 1];
- 确定策略记作\(\mu \mathcal{S}\rightarrowtail\mathcal{A}\),把状态s作为输出,直接输出动作\(a = \mu (s)\)。
-
强化学习是具有随机性的,随机性来源于动作、状态以及奖励:
- 动作的随机性来源与随机决策(策略);
- 状态的随机性来源于状态转移函数,即下一个状态具有随机性;
- 奖励也具有随机性,建立的随机性来源于动作或者动作+状态。
-
马尔可夫性质:下一时刻的状态仅依赖于当前状态和动作,而不依赖于过去的状态和动作。
-
轨迹(trajectory)是一回合中,智能体观测到的所有状态、动作、奖励;在符合马尔可夫决策过程(MDP)的环境中(完全观测环境)的轨迹中无未观测值,在部分观测环境中(缺失部分参数或真实状态s隐藏)的轨迹可能会有未观测值。
-
折扣率\(\gamma\)是对未来奖励进行时间加权的系数,随着时间逐渐累乘;MDP的回报期望可利用贝尔曼方程高效计算,非MDP回报可计算单条轨迹,但难求解期望。
-
MDP通常使用折扣汇报给未来的奖励作折扣,折扣可以被吸收到建立函数中,其与奖励函数有界性一起能保证回报的收敛。
-
折扣率让无限期任务的累计奖励收敛,引导Agent在短期收益和长期规划中找到平衡,未来具有不确定性,其本质上是对未来收益可信度的量化:\(U_t = R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \dots = \sum_{k=0}^{\infty} \gamma^k R_{t+k}\)
-
回报中的随机性来源于奖励,奖励的随机性来源于动作+状态,所以回报的随机性实际来源于策略与状态转移概率函数,即未来的动作和·状态。
-
为了排除策略对动作的影响,提出了最优动作价值函数\(Q_*(s_t, a_t) = \max_{\pi} Q_\pi(s_t, a_t) \forall s_t \in \mathcal{S},\ a_t \in \mathcal{A}.\),是指在状态s下执行动作a,之后遵循最优策略时,能获得期望的长期折扣回报。
-
如何区分是否是MDP取决于环境的状态转移是否满足马尔可夫性质,而非对环境动态先验知识是否已知,Agent缺乏对环境动态先验知识的是模型位置的MDP而非非MDP。
-
最优动作价值函数刻画的是所有可能轨迹的期望回报(长期平均回报),而非单条轨迹的期望回报;MDP的结构使得可以通过贝尔曼最优方程解出最优解,使得最优动作价值函数是有效的,是推导确定型最优策略的核心依据。
-
状态价值函数\(V_\pi(s_t) = \mathbb{E}_{A_t \sim \pi(\cdot \mid s_t)} \left[ Q_\pi(s_t, A_t) \right] = \sum_{a \in \mathcal{A}} \pi(a \mid s_t) \cdot Q_\pi(s_t, a)= \mathbb{E}_{A_t, S_{t+1}, A_{t+1}, \dots, S_n, A_n} \left[ U_t \mid S_t = s_t \right].\)是评估状态好坏的核心工具,描述在特定策略下,从某状态出发的长期期望回报;可以在对抗中衡量双方胜算,状态价值可以衡量策略与状态的好坏,其不依赖具体动作,是所有可能动作的价值在策略下的期望,最优状态价值函数即所有策略中能达到的最大状态价值。
-
之所以会在比赛中出现神之一手的反转,是因为状态价值函数计算的是从状态s出发,遵循策略的长期平均回报,但是单场比赛是单次轨迹,即在期望中被平均的低概率赢法会在单次对局中发生、对手策略的非最优解打破最优假设创造出超期望回报(状态价值函数一般计算对手策略的最优解),其次状态价值函数依赖对环境的建模(现实会出现关键信息未建模(即未被定义为状态的隐藏因素)、复杂现实简化建模等),还有比赛环境会出现动态变化、状态函数的核心追求长期平均而比赛追求单次胜利等原因。
-
总结15:状态价值函数的 “期望” 属性,决定了它描述的是 “长期规律”,而非 “单次事件的必然”。比赛中的反转,是 “期望的平均性” 与 “单次现实的偶然性 / 未被建模的复杂性” 共同作用的结果 —— 低期望不代表没机会,只是 “赢的概率低,但并非不可能”。
-
马尔可夫决策过程(MDP)通常是四元组\((\mathcal{S},\mathcal{A},\mathcal{p},\mathcal{r})\)其中\(\mathcal{S}\)是状态空间,\(\mathcal{A}\)是动作空间,\(\mathcal{p}\)是状态转移函数,\(\mathcal{r}\)是奖励函数。有时MDP指的是五元组 \((\mathcal{S},\mathcal{A},\mathcal{p},\mathcal{r},\gamma)\)。
-
价值函数是回报的期望;状态价值函数是指在状态s时之后一直按照策略\(\pi\)行动的价值;动作价值函数时在状态s时先进性动作a再按照策略\(\pi\)行动的价值,比状态价值函数更贴近动作选择。
-
强化学习的目的是寻找最优策略,最优策略对应的价值函数被称为最优价值函数;之所以基于价值的强化学习要聚焦于最优动作价值函数,是因为其直接指导动作选择而不依赖模型(多在无模型方法中使用),也是策略优化的终极目标(直接对应最优策略)。
价值学习
DQN与Q学习
-
Q学习的Q指Quality,是因为动作价值函数本质上是对状态s下选择动作a这一决策的质量评估。
-
已知 \(s_t\) 和 \(a_t\),不论未来采取什么样的策略 \(\pi\),回报 \(U_t\) 的期望不可能超过 \(Q_⋆\),所以我们在实践中,我们需要近似出\(Q_⋆\),只要有足够多的经验就可以训练出\(Q_⋆\)先知,所以提出了DQN网络,记作 \(Q(s, a; \omega)\)。
-
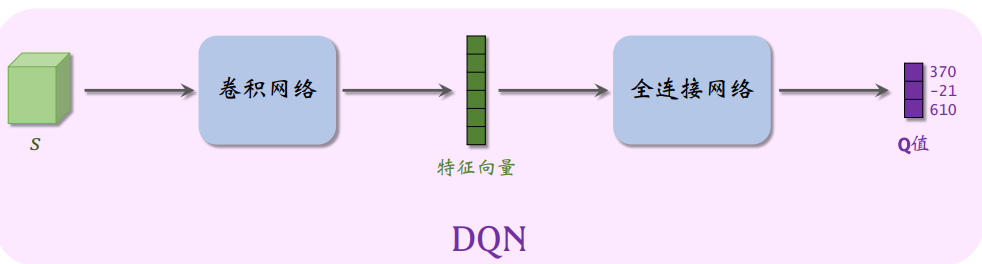
DQN的神经网络结构即:
-
DQN网络的主要作用就是预测\(\omega\)使得\(Q(s, a; \omega)\)尽量接近\(Q_*(s, a)\),DQN网络的输出是离散动作空间\(\mathcal{A}\)上的每个动作的评分,即\(|\mathcal{A}|\)维的向量,Q中的a对应的动作价值则是向量的一个元素;对动作最优函数的近似。
-
训练DQN最常见的算法是时间差分(TD),其机制是通过对当前经验+未来估计迭代优化Q网络对动作价值函数的估计(走一步就利用现有经验修正一步),比如从 状态 s→做动作 a→得到奖励 r→到新状态 s' 就立刻根据这一步的经历,更新对 “在 s 下做 a 好不好” 的判断。
-
TD为了避免学习到部分偏好(连续十步一个选择更好),把每一步的经历存到了经验池中,每次更新随机抽一批经历学习;其次为了固定目标(防止出现摆荡),一直基于校正后结果矫正会出现摆荡,用一个段时间不更新(固定)的网络做参照保持目标结果段时间稳定,会复制主网络作为参照网络(目标与主A,主段时间内根据目标的指导优化变成A+,目标复制主,此时主与目标A+;稳定参考->优化进步->更新参考->再优化)。
-
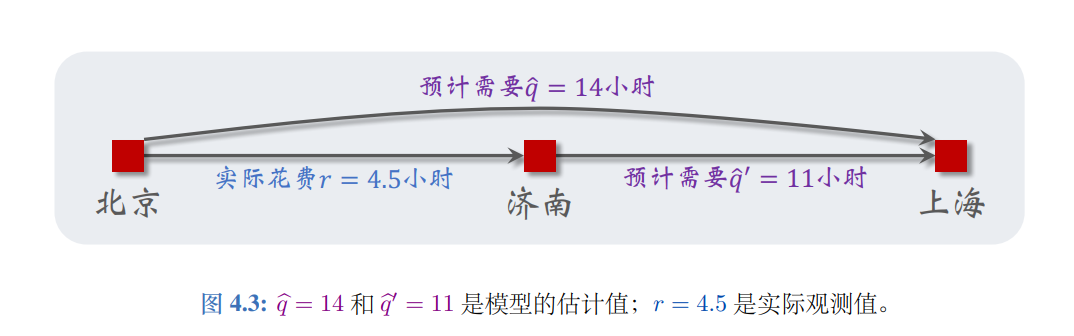
TD的误差是目标Q值(目标网络)与当前Q值(主网络)的差,误差是指导信号与当前的差,其实就是逐渐接近正确估计的过程(减少震荡),因为TD目标有更多事实的成分:
-
最优贝尔曼方程(由最优动作价值函数与回报推导得):
\[\begin{equation}\underbrace{Q^*(s_t, a_t)}_{\text{$U_t$的期望}} = \mathbb{E}_{S_{t+1} \sim p(\cdot \mid s_t, a_t)} \left[R_t + \gamma \cdot \underbrace{\max_{A \in \mathcal{A}} Q^*(S_{t+1}, A)}_{\text{$U_{t+1}$的期望}} \,\bigg|\, S_t = s_t, A_t = a_t \right]\end{equation} \] -
奖励\(r_t\)为什么会与\(s_{t+1}\)有关:\(r_t\)的核心作用是评价动作\(a_t\)的好坏,但是好坏必须有状态变化的结果\(s_{t+1}\)定义,即奖励是环境对“动作→状态变化”的打分,而“状态变化”的结果就是\(s_{t+1}\),因此奖励天然依赖 \(s_{t+1}\),即要有对未来的判断。
-
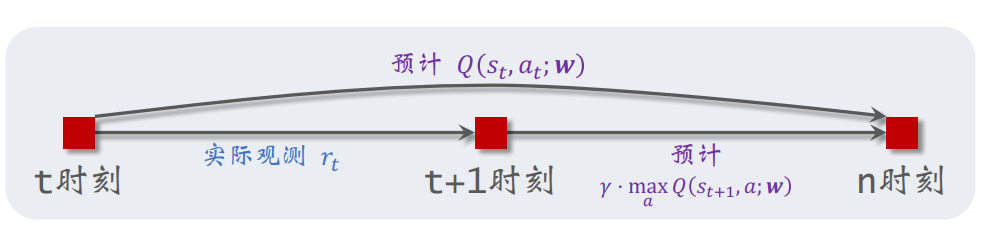
TD算法的实际loss推进可由以下公式表示,已知四元组\((s_t, a_t, r_t, s_{t+1})\),可用蒙特卡洛近似得:
\[\begin{equation} \underbrace{Q(s_t, a_t; \boldsymbol{w})}_{\text{预测}\ \hat{q}_t} \approx \underbrace{r_t + \gamma \cdot \max_{a \in \mathcal{A}} Q(s_{t+1}, a; \boldsymbol{w})}_{\text{TD目标}\ \hat{y}_t}\end{equation} \]
-
\(\boldsymbol{w} \leftarrow \boldsymbol{w} - \alpha \cdot \delta_t \cdot \nabla_{\boldsymbol{w}} Q(s_t, a_t; \boldsymbol{w}) \delta_t=\hat{q}_t - \hat{y}_t\)为DQN下降的函数,这里用MAE作为基础损失函数。
-
训练流程:用\((s_t, a_t, r_t, s_{t+1})\)算出DQN预测值\(\hat{q}_t\),还有TD目标\(\hat{y}_t\)、TD误差\(\delta_t\),用DQN下降函数更新DQN参数,这其中与策略\(\pi\)无关。
-
DQN`训练需要分成两个部分:收集训练数据、更新参数\(\omega\),更新参数时在经验回放数组中抽取参数更新,一般收集一次训练数据更新几次(可同时进行)。
-
收集训练数据可以用任何行为策略\(\pi\),常用的是\(\epsilon-\text{greedy}\)策略,即\(a_t = \begin{cases} \text{argmax}_{a} Q(s_t, a; \boldsymbol{w}), & \text{以概率 } (1-\epsilon); \\\text{均匀抽取 } \mathcal{A} \text{ 中的一个动作}, & \text{以概率 } \epsilon.\end{cases}\);
-
把一局游戏中的轨迹划成n个\((s_t, a_t, r_t, s_{t+1})\)四元组,存入经验回放数组。
-
TD算法分为Q学习和SARSA,Q 学习的目的是学到最
优动作价值函数\(Q_⋆\),而SARSA的目的是学习动作价值函数\(Q_{\pi}\)。 -
\(\mathcal{A}\)是有限集且\(\mathcal{S}\)是无限集的情况下可以用Q学习,而\(\mathcal{A}\)是无限集的情况下需要用连续控制的方法。
-
最早的Q学习都是用表格表示,即将S-A的所有情况放在一个表格中去,找到当前\(s_t\)对应的行选择相应动作执行,用一个表格近似最优表格然后用Q算法更新原表格,每次更新一个元素,最终收敛;方法即普通DQN的TD算法(更新逻辑从损失函数梯度下降变成表格,更新不需要目标网络);本质差异是由DQN用神经网络代替Q表解决了连续空间和高纬度的拓展性问题,并且用经验回放和目标网络解决了训练不稳定问题。
-
表格Q学习训练流程如下:在经验回放数组中抽取四元组,设置现有表格为\(\hat{Q}_{now}\),记录现有状态动作Q值\(\hat{q}_j = \tilde{Q}_{\text{now}}(s_j, a_j)\),记录\(s_{j+1}\)状态的最大Q值\(\hat{q}_{j+1} = \max_{a} \tilde{Q}_{\text{now}}(s_{j+1}, a)\),计算TD目标和TD误差\(\hat{y}_j = r_j + \gamma \cdot \hat{q}_{j+1}, \quad \delta_j = \hat{q}_j - \hat{y}_j\),更新表格\(\tilde{Q}_{\text{new}}(s_j, a_j) \leftarrow \tilde{Q}_{\text{now}}(s_j, a_j) - \alpha \cdot \delta_j\)。
-
行为策略是用于智能体和环境交互的策略,目标策略是强化学习最终的目的;在示例DQN中,目标策略是\(a_t = \text{argmax}_{a} Q(s_t, a; \boldsymbol{w})\),用任意行为策略收集经验训练该目标策略;可分为同策略/在线策略(On-policy) 与异策略/离线策略(Off-policy),即相同的行为策略和目标策略、不同的行为策略和目标策略。
-
行为策略随机的好处在于能探索更多没见过的状态,异策略的好处是可以用行为策略收集经验然后用经验回放的范式训练,经验回放只适用于异策略,因为同策略要求收集经验的行为策略需与当前目标策略一致。
-
目标策略在每个状态下选择的是“当前 Q 函数估计的最优动作”;当Q函数收敛到真实最优价值时,该动作即为真实最优动作。
-
更新一般是与步数强绑定而非episode,因为步数是更稳定的细粒度单位。
SARSA算法
-
SARSA也是一种TD算法,目的是学习动作价值函数\(Q_\pi(s_t, a_t)\),Q学习是异策略,而SARSA是同策略算法;即SARSA在学习时直接学习当前策略下的动作价值函数,并且更新时使用的时与生成动作相同的策略。
-
SARSA会使用执行的下一个动作的对应Q值(\(Q_{\pi}\))而非最大Q值(\(Q_*\)),即Q学习的是动作的最优价值函数(与策略无关),而SARSA学的是当前策略下下一个动作的Q值。
-
Q 学习的 Q 值反映了 “如果总是做出最优选择,这个动作有多好”,SARSA的 Q 值反映了 “在我的当前探索策略下,这个动作实际有多好”;Q学习在训练过程中对“风险”的忽视会导致学习到的最优策略在实际不确定性环境中执行时会表现出脆弱性(探索会有随机动作、高估动作价值),甚至无法收敛到真正最优解,而且是理论最优缺乏可执行性;所以在实际部署中SARSA更适合需要安全的场景。
-
表格SARSA算法如同表格Q学习,只不过将表格和策略函数相关联,策略函数变化表格也变化,通过更新近似\(Q_\pi\)每次更新一个元素从而达到收敛;表格SARSA的\(Q_{\pi}(s_{t}, a_{t})\)的近似函数\(q(s_{t}, a_{t})= r_t + \gamma \cdot Q_{\pi}(s_{t+1}, \tilde{a}_{t+1}).\)其中\(\tilde{a}_{t+1} \sim \pi(\cdot \mid s_{t+1}).\)动作是基于状态与策略的随机抽样;\(\widehat{y}_t \triangleq r_t + \gamma \cdot q(s_{t+1}, \tilde{a}_{t+1}).\)是TD目标;\(q(s_t, a_t) \leftarrow (1 - \alpha) \cdot q(s_t, a_t) + \alpha \cdot \widehat{y}_t.\)是更新函数。
-
SARSA是用到的是五元组\((s_t, a_t, r_t, s_{t+1}, \tilde{a}_{t+1})\),其中\(\tilde{a}_{t+1}\)是根据\(\pi(\dot | s_{t+1})\)抽样而来的;训练流程同DQN。
-
因为是同策略,每次更新策略时旧策略的经验就没有用了,所以SARSA算法必须一步一更新,这是其算法核心。
-
如果输入的状态s是张量或矩阵,那么用卷积网络处理s;如果s是向量,那么用全连接层处理s,价值网络即神经网络\(q(s,a;\omega)\)。
-
训练流程:

-
在获得TD目标\(\hat{y}_t\)中的\(r_t\)只有一个奖励,则称该为单步TD目标;若获得TD目标\(\hat{y}_t\)中的\(r_t\)只有\(m\)个奖励,则为多步TD目标。
-
\(m\)步TD目标的公式为:\(\widehat{y}_t \triangleq \left( \sum_{i=0}^{m-1} \gamma^i r_{t+i} \right) + \gamma^m \cdot q(s_{t+m}, a_{t+m}; \boldsymbol{w}).\),可由贝尔曼方程、回报公式、蒙特卡洛近似及单步TD推导得出。
-
当在训练时,用一句游戏进行到底观测到的所有奖励用回报作目标,那么最终的方法将不是TD,而是蒙特卡洛,即用\(u_t\)去近似期望而已。
-
蒙特卡洛算法是具有无偏性(\(u_t\)是无偏估计)和方差大(依赖于随机变量大)两种特性的,意味着蒙特卡洛在小空间低建立反差的情况下可以收敛到理论最优,但同时在实际表现中因为奖励反差大、大空间、无法获得完整episode等情况实际效果并不比TD强。
-
单步TD算法和多步TD算法:单步TD方差低、偏差高,多步TD方差高偏差低,可由12得;单步TD是在线更新(实时性)适合动态环境,多步TD则是离线更新(延迟性)适合建立延迟但可预测,在Q-learn中实时性和延迟性获得了缓冲而非消除;状态空间大适合用单步TD,否则多步TD的方差会进一步扩大。
-
自举就是用自己的估计去更新自己,在价值网络中则体现在价值网络用自己做出的估计更新价值网络自己;自举的单步TD的目标随机性只来自与一个状态空间与动作空间,而多步则是来自于n个;自举会使得偏差从\((s_{t+1}, a_{t+1})\)。
-
自举与蒙特卡洛的对比:

-
自举通常比蒙特卡洛收敛快,TD目标中既有自举也有蒙特卡洛(\(R_t\)),如果把m设置的较好,可以在方差和偏差间找到好的平衡,使得多步TD目标优于单步TD目标。
价值学习高级技巧
-
经验回放数组只保留最近b条数据(删除多余旧数据),超参数b会影响训练结果,一般设置为\(10^5 ~ 10^6\);在实践中,要等回放数组中存入足够多的四元组时才开始做经验回放(DQN用20万条,Rainbow DQN用8万条),回放数组中数量不够的时候DQN只与环境交互而不更新,否则会效果不好。
-
在经验回放中,一般用来随机抽取经验从而消除元组间相关性,重复利用经验会比不重复收敛更快,一般样本数量比更新次数更重要,更新次数只会影响训练计算量,而数量则是直接与收集强相关。
-
优先经验回放是经验回放的改进,比普通经验回放效果更好,优先经验回放根据权重进行非均匀随机抽样,应该给意外情况更高权重,即预测Q与真实Q的偏差越大权重越大:有两种抽样方法,第一种是\(p_j \propto \vert \delta_j \vert + \epsilon.\),第二种先对TD误差做降序rank,即\(p_j \propto \frac{1}{\text{rank}(j)}.\);因为抽样的概率不同,可以通过调整学习率来抵消偏差,即\(\alpha_j = \frac{\alpha}{(b \cdot p_j)^\beta}\),\(b\)是数组中样本总数\(\beta\)是一个需要调整的超参数,一般由小到大直到1。
-
学习率减小不意味着对权重的抵消,而是对样本更好的利用,多次学习相当于对噪声梯度的平均,降低了梯度噪声的干扰,让参数越稳定(类似于mini batch)。
-
在DQN利用非均匀采样的优先经验回放时,每次采样时应该利用新的参数重新估计其TD误差并更新数组中其的值。
-
TD算法自举带来的偏差会随着TD目标的定义估计传播,从而让更多价值获得偏差(被高估或被低估);同时噪音+最大化会导致高估,因为实际DQN的输出\(Q_*(s, a;\omega)\)是真实价值\(Q_*(s, a)\)加上随机噪音\(\epsilon\),而且DQN的输出是真实价值的无偏估计\(\mathbb{E}_{\epsilon} \left[ \max_{a \in A} Q(s, a; \boldsymbol{w}) \right] \geq \max_{a \in A} Q_{\star}(s, a)\),所以最大期望回报实际是大于最大实际期望的,从而会带来高估。
-
高估本身不是问题,如果高估是均匀的话;但在实践中高估是不均匀的,因为对不同动作状态的学习频率不一样,所以高估的学习程度也不一样,从而导致高估真正的弊端,即某个状态下有动作期望回报相对大但实际回报相对小。
-
总结6:实际高估原因:TD算法自举会导致偏差的传播,TD目标内包含一项最大化导致高估。
-
第一个解决方法是目标网络(target-DQN),使用里一个神经网络(\(Q_*(s, a;\omega^-)\))计算TD目标代替主网络,可以切断自举,从而缓解自举造成的偏差。
-
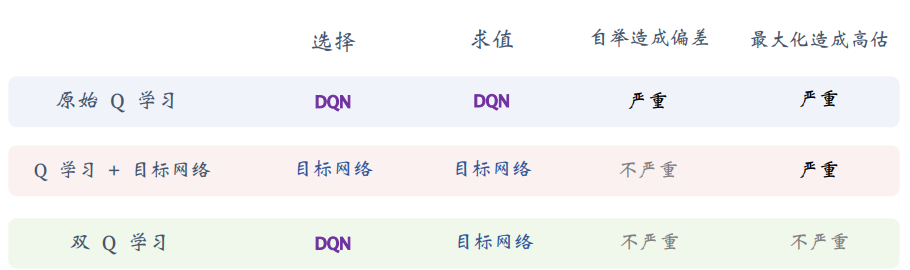
双Q学习(double DQN:DDQN)算法:与target-DQN一样,只是一种训练DQN的TD算法,与DQN无区别;对TD目标求值的最大化可以拆分成两步,即选择动作\(a\)、求值TD目标;原始的DQN选择和求值都用DQN,DDQN学习主网络选择、目标网络求值;如果用目标网络选择的话,就会出现用旧策略选择动作用新估计价值,不符合学习当前最优策略的逻辑;如果主网络选择又评估就会导致选择夸大又重新评估夸大,就会导致滚雪球一样放大错误,即\(\underbrace{\widetilde{y}_t = Q(s_{j+1}, a^\star; \boldsymbol{w}^-)}_{\text{双Q学习}} \leq \underbrace{\widehat{y}_t = \max_{a \in \mathcal{A}} Q(s_{j+1}, a; \boldsymbol{w}^-)}_{\text{用目标网络的Q学习}}\)。
-
三种TD算法对比:
-
对决网络(dueling network)的基本思想是将最优动作价值\(Q_*\)分解成最优状态价值\(V_*\)加最优优势\(D_*\);最有优势函数的定义是:\(D_{\star}(s,a) \triangleq Q_{\star}(s,a) - V_{\star}(s)\),最优动作价值函数衡量的是该状态\(s\)下采取动作\(a\)的最大期望回报,而最优状态价值函数则是衡量状态\(s\)下能获得最大值,即\(V_{\star}(s) = \max_{a} Q_{\star}(s,a)\);最优优势函数则是代表最优动作价值函数与最优状态价值函数的差,所以其差值实际上是在状态\(s\)下选择动作\(a\)相对于最优价值行动的优势(即比最优动作好多少),同时可得\(\max_{a \in \mathcal{A}} D_{\star}(s,a) = 0\),即定理:\(Q_{\star}(s,a) = V_{\star}(s) + D_{\star}(s,a) - \underbrace{\max_{a \in \mathcal{A}} D_{\star}(s,a)}_{\text{恒等于零}}, \quad \forall s \in \mathcal{S}, a \in \mathcal{A}.\)。
-
对决网络由两个神经网络组成,一个网络记成\(D(s,a; \omega^D)\),是对最有优势函数的近似,一个记成\(V(s;\omega^V)\);,是对最优状态价值函数的近似;最优动作价值函数\(Q_*\)可以近似为\(Q(s,a; \boldsymbol{w}) \triangleq V(s; \boldsymbol{w}^V) + D(s,a; \boldsymbol{w}^D) - \max_{a \in \mathcal{A}} D(s,a; \boldsymbol{w}^D)\)(即对决网络),参数记作\(\boldsymbol{w} \triangleq (\boldsymbol{w}^V; \boldsymbol{w}^D)\),如图:
 。
。 -
网络架构详解:状态通过卷积网络提取未特征向量作为优势头和状态价值头的输入,优势头的输出即为动作空间维度大小的向量,即\(D(s, a; \omega^D)\),状态头的输出则是一个状态标量\(V(s; \omega^V)\),可由13中神经网络公式推出近似最优价值,这涉及到设计神经网络的本质,即设计架构引导网络的学习(思考)方式而非单纯的理论推导。
-
既然\(\max_{a \in \mathcal{A}} D_{\star}(s,a) = 0, \quad \forall s \in \mathcal{S}\),之所以要将其写入等式中,是为了解决不唯一性(防止V、D随意上下波动不影响输出:\(V(s; \boldsymbol{w}^V) + D(s, a; \boldsymbol{w}^D) = V(s; \tilde{\boldsymbol{w}}^V) + D(s, a; \tilde{\boldsymbol{w}}^D)\),即解决角色识别问题),在实际应用中可以用mean代替max,可以增强训练稳定性减小偏差。
-
对决网络相对于DQN可以更好地学习到状态本身的价值信息以及动作相对于其他动作的优势,从而更高校地利用状态信息;减少了对动作重复估计状态信息的冗余,使得网络更快地学习到有价值的信息,更快收敛;面对状态相似但动作价值不同的情况下决策更准;对状态理解更深,泛化能力更强。
-
噪音网络(noisy net)为神经网络注入噪音让DQN获得更强的鲁棒性;将参数\(\omega\)替换成\(\mu + \sigma \circ \xi\),即

\(\mu、\sigma\)分别是均值和标准差,而\(\xi\)是服从标准正态分布\(\mathcal{N}(0, 1)\)的随机噪音,即\(w_{ij} = \mu_{ij} + \sigma_{ij} \cdot \xi_{ij}\),将参数包括bias替换为带噪音参数。 -
噪音DQN记作:\(\widetilde{Q}(s,a,\boldsymbol{\xi};\boldsymbol{\mu},\boldsymbol{\sigma}) \triangleq Q(s,a;\boldsymbol{\mu}+\boldsymbol{\sigma} \circ \boldsymbol{\xi})\),\(\xi\)在每次途径时(计算TD目标)会随机生成,但是在预测时,一般不采用噪音以获得最佳状态(将\(\sigma\)置为0);噪音DQN本身具有随机性,所以行为策略可以使用\(a_t = \underset{a \in \mathcal{A}}{\operatorname{argmax}} \widetilde{Q}(s,a,\boldsymbol{\xi};\boldsymbol{\mu},\boldsymbol{\sigma})\)。
-
使用噪音的根本目的是训练网络学习对参数波动(带有噪音)的容忍,使得即使有噪音干扰也不会出现大幅度预测偏离,即增加网络的鲁棒性;因为在实际应用中,环境本身存在不确定性,同时增加噪音促进探索反而可能降低复杂环境中的偏差,其根本目的有增强探索能力、提高样本效率、适应非平稳环境、端到端学习(不手动调整行为策略参数)。
实战
-
状态空间:状态空间不仅仅指视野域,还有所有会影响智能体决策的关键信息,但在实际中,状态空间的选择应该遵循完整性(包含所有)、最小充分性(避免冗余重复)、可观测性(实际感知到的信息)、稳定性(固定维度:维度时间上保持一致)原则,可包含数值特征、独热编码、矩阵、序列信息(经过RNN、LSTM处理的时序信息)等。
-
在表格Q学习中,输入的State是SIZE,而DQN等网络中是DIM。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号