Codeforces Round #429 (Div. 2) C. Leha and Function

C. Leha and Function

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Leha like all kinds of strange things. Recently he liked the function F(n, k). Consider all possible k-element subsets of the set [1, 2, ..., n]. For subset find minimal element in it. F(n, k) — mathematical expectation of the minimal element among all k-element subsets.

But only function does not interest him. He wants to do interesting things with it. Mom brought him two arrays A and B, each consists of m integers. For all i, j such that 1 ≤ i, j ≤ m the condition A_i ≥ B_j holds. Help Leha rearrange the numbers in the array A so that the sum 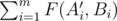is maximally possible, where A' is already rearranged array.

Input

First line of input data contains single integer m (1 ≤ m ≤ 2·10⁵) — length of arrays A and B.

Next line contains m integers a₁, a₂, ..., a_m (1 ≤ a_i ≤ 10⁹) — array A.

Next line contains m integers b₁, b₂, ..., b_m (1 ≤ b_i ≤ 10⁹) — array B.

Output

Output m integers a'₁, a'₂, ..., a'_m — array A' which is permutation of the array A.

Examples

Input

5 
7 3 5 3 4
 2 1 3 2 3

Output

4 7 3 5 3

Input

7 
4 6 5 8 8 2 6
 2 1 2 2 1 1 2

Output

2 6 4 5 8 8 6


题意：输入两个区间长度为m的集合A、B，重新构造集合A成为A’，使得A’集合中所有长度为A’[i]的1....n集合的所有长度为B[i]的子集的最小值的期望之和最大。
题解：A集合中的最大值依次对应B中的最小值。


代码：
#include <cstdio>
#include <algorithm>
using namespace std;
struct num{
	int id;
	int nu;
}c[210000];
bool cmp(num x,num y){
	return x.nu<y.nu;
}
bool cmp1(int x,int y){
	return x>y;
}
int main(){
	int n;
	int a[210000],b[210000];
	scanf("%d",&n);
	for(int i=0;i<n;i++){
		scanf("%d",&a[i]);
	}
	for(int i=0;i<n;i++){
		scanf("%d",&c[i].nu);
		c[i].id=i;
	}
	sort(a,a+n,cmp1);
	sort(c,c+n,cmp);
	for(int i=0;i<n;i++){
		b[c[i].id]=a[i];
	}
	for(int i=0;i<n;i++){
		if(i==0)	printf("%d",b[i]);
		else printf(" %d",b[i]);
	}
	printf("\n");
	return 0;
}