算法竞赛经典例题

 

村庄债务问题

有一个村庄，村里有n户人家，他们整整齐齐地排成一列，编号从左向右依次是1~n

他们当中，有的欠别人钱，有的则被别人欠钱。今天，村委会决定统一处理这些债务。

然而这个村庄有一个神奇的特性，钱只能在相邻的人家之间流动，也就是说对于第i户，他的钱只能给第i-1户或第i+1户

如果1欠了3的钱，则必须先把钱给2，再由2给3

现在村委会想知道，他们至少需要多少次付钱的操作才能把所有债务问题解决。

输入

第一行，一个整数n

第二行n个整数，第i个数v[i]代表第i户人家的债务情况。正代表欠钱，负数代表被欠钱。

n<=1e5

v[i]<=1e9

输出 一个整数 表示最少的流动量

样例

输入

5

3 0 0 0 -3

输出

12

解释

1给2   3块钱 流动量+=3

2给3   3块钱 流动量+=3

3给4   3块钱 流动量+=3

4给5   3块钱 流动量+=3

流动量=12

 

 

这道题实际上是在说，经过若干次操作，一个东西由一个状态变成另外一个状态。而最终状态比较特殊，要求所有人既不欠钱，也不被欠钱。

也就是说所有v[i]都等于0

所有......v[i]......?有点麻烦，不如换个思路想想，v[i]=0对于任意i∈[1,n]均成立，那么对于i=1肯定成立

为什么要这么想呢，因为1的特殊位置，他只能和2发生关系，无论欠钱还是被欠钱，都只能通过2和别人交换。

但是对于2~n-1来说，他的左邻右舍都可以和他进行交换，问题会比较复杂。

所以我们先从最边上的1号入手

那么就不难想到一个算法

ans=0

for i=1 To n-1

　　ans+=abs(v[i])    //abs表示绝对值

　　v[i+1]+=v[i]

　　v[i]=0

print(ans)

 

翻转游戏(洛谷P1764)

就不写题面了，直接贴传送门(其实就是我懒得打了)

https://www.luogu.com.cn/problem/P1764

为了方便讨论，定义f(i,j)操作为:

　　翻转第i行第j列的棋子

　　翻转(i,j)上下左右的四个棋子

定义操作F(S)为:

　　对于所有(i,j)∈S

　　　　f(i,j)

可以想到一个O(2^n*n)算法

枚举全体棋子的子集S对S中所有棋子进行f操作。操作完检查是否为同一种颜色

不过这个算法严重超时，一个世纪都跑不完(不排除一个世纪以内出现可以快速跑完这个算法的计算机)

不要被他的[提高+/省选-]的难度吓到，其实思路和刚才的题一样

所有的棋子都变成一种颜色，哪就先考虑全变成黑色，讨论出全是黑色的算法，那么白色同理

全是黑色，就意味着第一排的所有棋子都是黑色

为什么这么想呢？因为想要影响第一行，只有在第一行操作也就是f(1,1),f(1,2),f(1,3)...f(1,n)和在第二行操作，即f(2,1),f(2,2),f(2,3)...f(2,n)只有两行

然而对于第i行(i∈[2,n-1])能影响它的是第i-1行的操作,第i行的操作,第i+1行的操作，共三行

是不是像极了上一题？

这样就可以优化一下那个一个世纪都跑不完的算法了

原算法枚举了所有棋子的子集，我们可以枚举第一行棋子的子集S₁

做一次F(S₁)

等等，这样下来第一行很有可能是乱七八糟的啊

不要急，刚才说了，第一行可以被第一行和第二行的f操作影响，进行完F(S₁)后，我们就不再直接操作第一行了

那么想把第一行全部变成黑色，只能通过操作第二行影响第一行

并且由于不再操作第一行了，那么想让第一行达到全黑，就可以确定唯一的第二行的子集S₂使得F(S₂)过后，第一行是全黑

F(S₂)过后，第一行全黑，第二行很有可能是乱七八糟的，但这时候已经不能操作第一行和第二行了，只能通过操作第三行影响第二行

于是就可以确定唯一的第三行子集S₃使得F(S₃)过后，第二行是全黑

以此类推，可以由S₁确定S₂~S_n

在进行完S_n以后，1~n-1一定是全黑的，虽然第n行很可能是乱七八糟的,但  如果存在解，那么一定能枚举到一个S₁使得第n行在操作完以后是全黑的

如果找不到，那么无解

伪代码如下

ans=+∞;

for S₁⊆第一行:

　　F(S₁)

　　temp=|S₁|          //|S1|表示S₁的元素个数

　　for i=2 to n

　　　　for j= 1 to n

　　　　　　if (i-1,j)是白色:

　　　　　　　　f(i,j)

　　　　　　　　temp++

　　if 第n行全黑

　　　　ans=min(ans,temp)

if (ans<+∞) print(ans)

else print("Impossible")

顺序对计数

给定一个长度为n的序列a，求有多少(i,j)满足i<j且a[i]<a[j]

经典题目，用树状数组可以解决，这里就不详细说了(其实还是因为懒)

三元组计数

 

给定一个长度为n的序列a，求有多少(i,j,k)i<j<k且满足a[i]<a[j]<a[k]

n<=1e5

这是顺序对的加强版

这道题要从 j 上下手，数据规模提示我们时间复杂度应该是O(n)或O(nlogn)并且这是一个计数问题，算法的大体思路就是把a中所有的元素枚举一遍，对(i,j,k)进行统计

我们要枚举的正是j

为什么要枚举中间元素j呢？

如果我们能够知道对于每个j，有几个i满足i<j且a[i]<a[j]，以及有几个k满足k>j且a[k]>a[j]

对于每个j，把满足条件的i的个数记作x[j],把满足条件的k的个数记作y[j]

那么答案就等于

Σx[i]*y[i]

接下来就是如何统计x数组和y数组

如果你会用树状数组求顺序对的话，这一步就很简单了

 

 

马拉松（题目来源：LUTECE)

 

由于LUTECE信号不好，就直接把题面贴过来了

一年一鸽的电子科技大学 IUPC 校队马拉松开始了！共有 n 名 IUPC 校队成员参加这场马拉松，所有人个人运动的速度是恒定的，并且可以被分解为 vx[i]和vy[i]

在0时刻，所有队员都出现在直线y=ax+b上

由于 IUPC 的优良传统，对于第 i 位成员，他每碰到一位其他成员（同一时刻出现在同一位置），他就会施展膜大佬技能，使自己的的膜法值加 1

现假设 IUPC 校队成员精力十足，从负无穷时刻开始跑，一直跑到正无穷时刻。zhw 大佬想知道所有参赛成员的膜法值之和是多少

 

Standard Input

 

第一行三个整数 n,a,b

接下来 n 行每行三个整数x[i] vx[i] vy[i]

 

Standard Output

 

一行一个整数代表答案。

 

 

 

说实话，拿到这道题的时候我懵逼了几分钟，随后我意识到了“所有人的起点都在一条直线上” 是一条多么重要的性质。

随后我想到了，相撞关系是不是具有传递性？也就是说a撞b，b撞c，那么a一定撞c？

答案是肯定的

你可以用代数方法证明，也可以用这种比较直观的证明方法证明

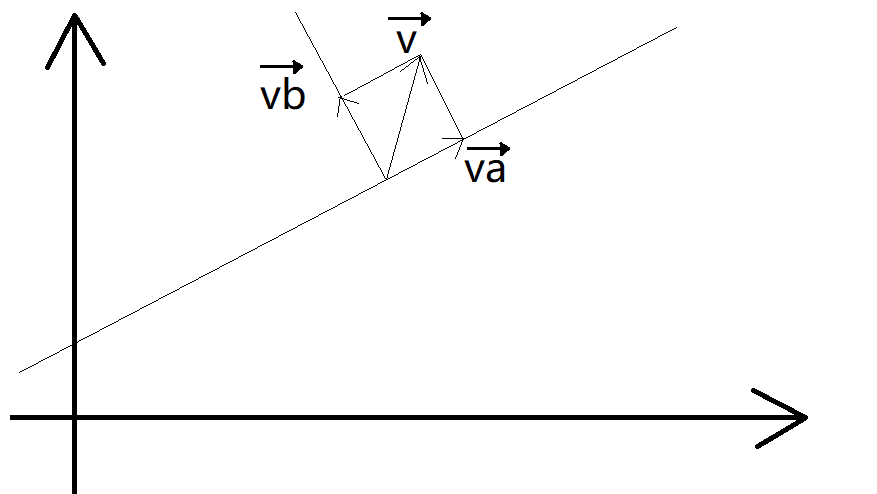
把一个人的速度v分解成沿直线方向 向右的速度va和垂直于直线方向 向上的速度vb  (v,va,vb均为向量)

那么显然，|vb|相同且|va|不同的人一定会相撞(想想这是为什么)

直接把所有人以|vb|为第一顺序，以|va|为第二顺序排序

从左到右扫一遍，就能统计出答案

因为已经排好序了，|vb|相同的人已经排在了一起，分别扫描每一段|vb|相同的人，扫描的同时维护前面有几个人的|va|与当前正在扫描的人的不同(记为pre)，每次ans+=pre*2即可

这道题的出题人可能不希望题目太毒瘤，把时间区间设为负无穷到正无穷，也就是说相撞时间可以为负的。如果时间只能为正，该怎么做呢？

把所有人以|vb|为第一顺序，以横坐标为第二顺序排序

如果两个人a,b的|vb|相同，a的横坐标<b的横坐标且a的|va|大于b的|va|那么他们会相撞

你想到了什么？

逆序对！

于是这道题的毒瘤加强版算法就这么出来了