leetcode 84. 柱状图中最大的矩形

题目描述：

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

 

 

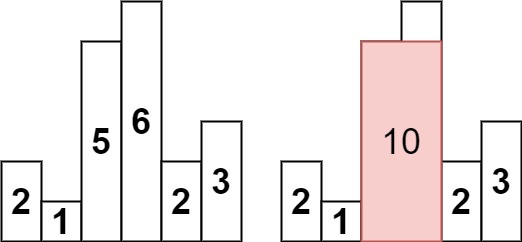
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

解题思路：

看题目本身，跟经典的接雨水有点类似。但不同点是接雨水的高度是由左右边界的最小值决定，这题的高度则是由每个柱子本身决定。

1. 暴力解法：自己能想到的解法。由当前柱子向左右两边延伸，只要满足高度大于当前柱子的，就能继续延伸，直到遇到高度小于当前柱子或到达边界。这实际上是以每个柱子为中心，向左右去寻找当前柱子的边界，将边界作为矩形宽度，柱子高度为矩形长度。最后取面积最大的矩形为最终结果。时间复杂度O(n^2)，会超时。

 

2. 单调栈：大四算法课上单独讲过这类算法。实际是拿空间换时间，维护一个单调递增的栈，一定程度上是保证了左边界，再通过遍历的方式寻找右边界。始终维护一个单调递增的栈，遇到小于栈顶元素高度的柱子，则需要将栈顶元素出栈，也就意味着对于当前栈顶的元素来说，找到了其左右边界，左边界就为栈的下一个元素（若不存在则边界为-1），右边界为当前遍历到元素。当遍历结束后，需要清空栈，此时的右边界的确定的，为数组的长度，需要确定的是左边界，同样为栈的下一个元素（若不存在则边界为-1）。

 

代码：

解法一：

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size();
        int ans = 0;
        for(int i=0; i<n; i++) {
            int l = i;
            int r = i;
            while(l>=0 && heights[i] <= heights[l]) {
                l--;
            }
            while(r<n && heights[i] <= heights[r]) {
                r++;
            }
            if(r>=n)
                r = n-1;
            else if(r != i)
                r = r-1;
            
            if(l<0)
                l=0;
            else if(l != i)
                l = l+1;
            int area = heights[i]*(r-l+1);
            ans = max(ans, area);
        }
        return ans;
    }
};

　　

解法二：

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size();
        stack<int> s;
        int ans = 0;
        for(int i=0; i<n; i++) {
            while(!s.empty() && heights[s.top()] > heights[i]) {
                int tmp = s.top();
                s.pop();
                int length = heights[tmp];
                int weight = i;
                if(!s.empty())
                    weight = i-s.top()-1;
                ans = max(ans, length*weight);
            }
            s.push(i);
        }
        
        int length = 0;
        int weight = n;
        while(!s.empty()) {
            int tmp = s.top();
            s.pop();
            length = heights[tmp];
            weight = n;
            if(!s.empty())
                weight = n-s.top()-1;
            ans = max(ans, length*weight);
        }
        
        return ans;
        
    }
};