浅说树状数组

树状数组

树状数组作为信竞中又一个较为简洁的数据结构，也是非常的有用且好玩，虽然实用性没有线段树那么广，但是架不住它代码短啊！

引入

现在我们要维护一个数组，使其可以做修改和查询区间和。怎么做？

很显然，我们可以使用之前学过的分块来做，但是呢时间复杂度为 \(\cal O(n\sqrt n)\)，一旦我的 \(n\) 大于 \(10^6\) 不久寄了？那么我们怎么做呢？

查询

看到 \(10^6\) 这个数，是不是有一种直觉会用 \(\cal O(n\log n)\) 的算法，而看到 \(\log n\) 会想到什么？二叉树！对吧。那么对于一个区间，我们是不是就可以直接得到如下的图：（注：最后一排为我们要求的区间）

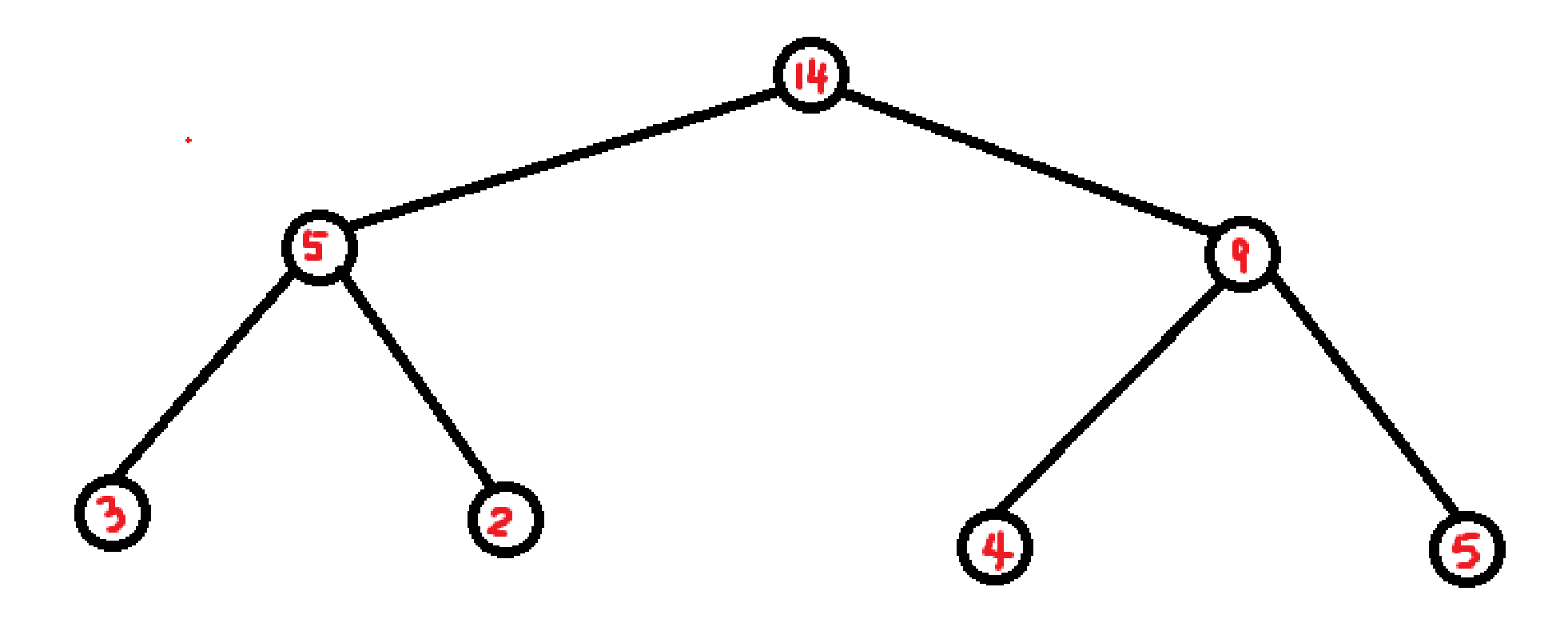
image

比如说我们要求区间[1,3]的区间和，是不是只需要求节点2和节点6的值？这样是不是就会快很多？

但是我们会发现很多的值用不到，比如说我要求区间[2,2]的区间和，我们完全没有必要去求节点5，我们只需要求节点2减去节点4的值是不是就可以了（类似于前缀和的思想）

又因为任意一个数都可以被唯一表示成一个二进制数，所以说我们就可以把一个前缀和分解成多个 \(2^n\) 大小的区间来表示。
例如：\(11=2^3+2^1+2^0\)，那么我们就可以这样表示：节点 \(x\) 的数组表示以 \(x\) 结尾，长度为 \(lowbit(x)\) 的区间和。

其中 \(lowbitx(x)\) 表示在二进制下的最后一个1的位数 \(k\) 和这个1后面的所有的0所组成 \(2^k\)，比如说 \(\because 10=(110)_2\therefore lowbit(10)=2\)。

而如何快速求 \(lowbit\) 呢？我们要从定义出发，很显然，我们将 \(x\) 取反再加1，就得到的 \(-x\) 的二进制数，我们发现，如果此时对这两个数做与运算的操作，我们就可以的到最后的1的位数，例如，\(6\) 的二进制编码是 \(110\)，全部取反后得到 \(001\)，加 \(1\) 得到 \(010\)。

\(proof:\) 设原先 x 的二进制编码是 (...)10...00，全部取反后得到 [...]01...11，加 1 后得到 [...]10...00，也就是 -x 的二进制编码了。这里 x 二进制表示中第一个 1 是 x 最低位的 1。

(...) 和 [...] 中省略号的每一位分别相反，所以 x & -x = (...)10...00 & [...]10...00 = 10...00，得到的结果就是 lowbit。

这样呢我们就可以用 \(\cal O(n)\) 的空间复杂度装下整个区间，而当我们要求一段区间和的时候，我们就可以用类似于前缀和的思想来进行操作。这样听起来是不是有一点抽象，我们可以画个图来感受一下：

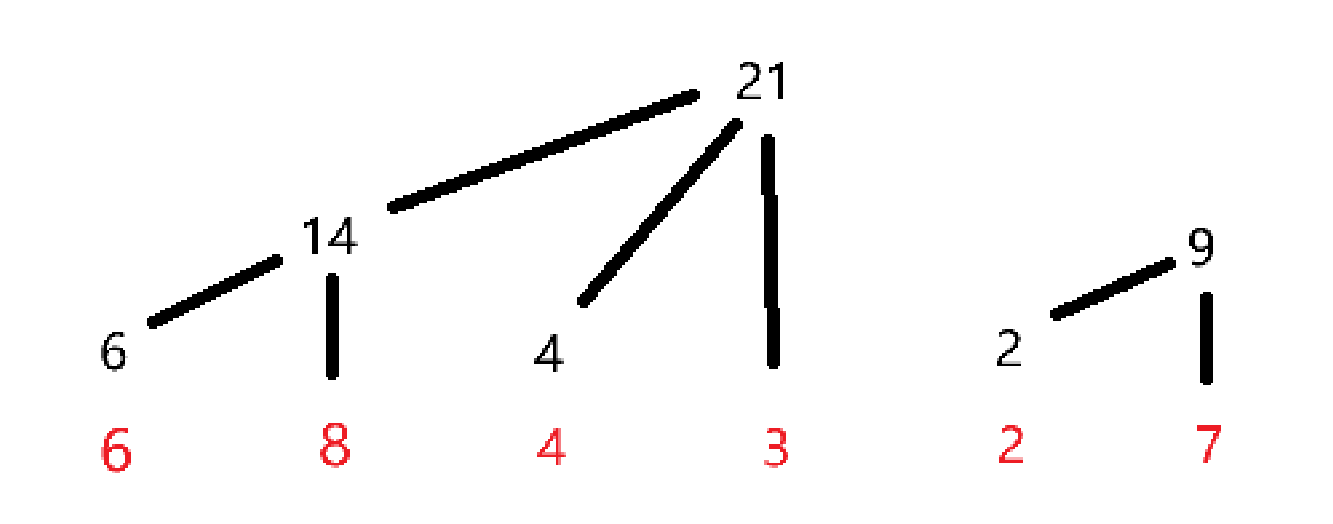
image

比如说我们要求[3,5]，我们实际上就是求[1,5]-[1,2]，而[1,5]是 \(tree[4]+tree[5]=21+2=23\)，同时[1,2]是 \(tree[2]=14\)，那么[3,5]就是 \(23-14=9\)。这个还是比较好理解的对吧，下面给出示范代码：

inline int lowbit(int x){
    return x&(-x);
}

void query(int n){
    int cnt=0;
    while (n>0){
        cnt+=tree[n];
        n-=lowbit(n);//每一次取到当前管辖的范围
    }
 	/*
 	也可以这样写
 	for (int i=n;i>0;i-=lowbit(i)){
 		cnt+=tree[i];
 	}
 	*/
    return cnt;
}

修改

我们现在可以完成查询的操作了，但是很显然，如果说我们只查询不修改的话，完全没有必要用树状数组，我们使用前缀和就可以很好的解决了，因此我们现在要看的是如何进行修改操作。很显然，我们的修改操作会分为两个部分，一个是单点修改，一个是区间修改。

单点修改

我们所要修改的，本质上就是寻找改变了一个值后，会影响的数组，也就是看这个点被哪些区间所管辖了。很显然，管辖 \(a[x]\) 的 \(tree[y]\) 一定包含 \(tree[x]\)，那么我们每一次就网上跳一个 \(lowbit(x)\) 不久可以了吗？然后重复这个操作，直到超出了数组的范围停止。

下面给出示范代码：

inline void update(int x,int val){
    while (x<=n){
        tree[x]+=val;
        x+=lowbit(x);
    }
    /*
    也可以这样写
    for (int i=x;i<=n;i+=lowbit(x)){
    	tree[i]+=val;
    }
    */
}

这里要注意一下，因为这里的例子是区间和，所以代码中写的是 \(tree[x]+val\) ，而在题目中，可能不是加法，有可能是其他的定义，具体的要根据题目具体分析，但是这些都符合一个特征，就是满足结合律，比如说加法满足结合律，乘法满足结合律，但是除法就不满足结合律了。

区间修改

区修单查

我们先由浅入深来思考这个问题，如果是区间修改，单点查询怎么做？由于我们不可能一个个去对这个区间内的数进行修改，所以说我们得用一种快速的方法来解决，而提到区间修改，我们会想到什么？差分对吧！那么我们是否可以通过维护差分的方式来维护整个数组呢？

很显然是可以的，由于 \(a[i]=\sum_{j=1}^ic[j]\)，再结合之前差分的知识，我们实际上是可以把这个区间修改等效为两个单点修改的，也就是 \(update(l,x)\) 和 \(update(r+1,-x)\)，这是很显然的差分思想，然后我的树状数组维护这个差分就可以了，当我要单点查询一个值 \(i\) 的时候，就只需要求[1,i]的和就可以。我们可以稍微模拟一下：

模拟过程
初始状态

原数组 A = [0, 0, 0, 0, 0]（索引从 1 开始）
差分数组 D = [0, 0, 0, 0, 0, 0]（多开一个位置方便处理边界）
树状数组 BIT 初始化为全 0

操作 1：区间 [2,4] 加 3

  1. 对差分数组的影响：

    • D[2] += 3
    • D[5] -= 3（因为 R+1=5）

  2. 更新树状数组：

    • 更新位置 2：
      • i=2，BIT[2] += 3
      • i += lowbit(2)=2，i=4，BIT[4] += 3
      • i += lowbit(4)=4，i=8（超出范围，停止）
    • 更新位置 5：
      • i=5，BIT[5] -= 3
      • i += lowbit(5)=1，i=6，BIT[6] -= 3
      • i += lowbit(6)=2，i=8（超出范围，停止）

  3. 树状数组当前状态：

    BIT[1]=0, BIT[2]=3, BIT[3]=0, BIT[4]=3, BIT[5]=-3, BIT[6]=-3, BIT[7]=0, BIT[8]=0
操作 2：区间 [1,5] 加 2

  1. 对差分数组的影响：

    • D[1] += 2
    • D[6] -= 2（因为 R+1=6，超出原数组长度）

  2. 更新树状数组：

    • 更新位置 1：
      • i=1，BIT[1] += 2
      • i += lowbit(1)=1，i=2，BIT[2] += 2
      • i += lowbit(2)=2，i=4，BIT[4] += 2
      • i += lowbit(4)=4，i=8（超出范围，停止）
    • 更新位置 6：
      • i=6，BIT[6] -= 2
      • i += lowbit(6)=2，i=8（超出范围，停止）

  3. 树状数组当前状态：

    BIT[1]=2, BIT[2]=5, BIT[3]=0, BIT[4]=5, BIT[5]=-3, BIT[6]=-5, BIT[7]=0, BIT[8]=0
操作 3：查询位置 3 的值
  1. 单点查询 A [3] 等价于求差分数组 D 的前 3 项和
  2. 使用树状数组的 query 函数计算前 3 项和：
    • i=3，累加 BIT [3]=0
    • i -= lowbit(3)=1，i=2，累加 BIT [2]=5
    • i -= lowbit(2)=2，i=0，停止
    • 总和为 0+5=5
  3. 验证结果：
    • 原数组经过两次操作后：
      • 操作 1 后：A [2-4] 各加 3 → A=[0,3,3,3,0]
      • 操作 2 后：A [1-5] 各加 2 → A=[2,5,5,5,2]
    • 位置 3 的值确实为 5，与查询结果一致

下面给出示范代码：

//tree中维护的是差分
void update(int p,long long x){
	while (p<=n){
		tree[p]+=x;
		p+=lowbit(p);
	}
}

long long query(long long x){
	long long ans=0;
	while (x>=1){
		ans+=tree[x];
		x-=lowbit(x);
	}
	return ans;
}

区修区查

较为简单的区修单查解决了，那么区间修改，区间查询怎么做呢？首先可以想到，肯定还是要使用差分，然后我们就是要观察了。

首先还是差分前缀的问题，要查询的区间内，每一个点 \(i\) 都是 \(\sum_{j=1}^itree[j]\)，那么把整个区间都合起来，是不是就有 \(\sum_{i=l}^r\sum_{j=1}^i tree[j]\)，然后把这个式子转换为前缀差分，有 \(\sum_{i=1}^r\sum_{j=1}^i tree[j]-\sum_{i=1}^l\sum_{j=1}^i tree[j]\)，因此，我们只需要研究 \(\sum_{i=1}^x\sum_{j=1}^i tree[j]\) 这个式子就可以了（表示[1,x]的区间和）。

我们把这个式子纵向展开：（为了简便，我们设 \(x=5\)）

\[a[1]=tree[1]\\a[2]=tree[1]+tree[2]\\a[3]=tree[1]+tree[2]+tree[3]\\a[4]=tree[1]+tree[2]+tree[3]+tree[4]\\a[5]=tree[1]+tree[2]+tree[3]+tree[4]+tree[5] \]

可以发现每一个 \(tree[i]\) 都被计算了 \(x-i+1\) 次，那么就有 \(\sum_{i=1}^xtree[i]\times(x+1)-\sum_{i=1}^xtree[i]\times i\)。很显然，因为有 \(update\) 的缘故，我们不能通过 \(tree[i]\) 推出 \(tree[i]\times i\)，因此，我们就需要维护两个树状数组，分别存储。

然后到时候查询的时候，就把两个加起来就可以了。下面给出示范代码：

//tree1维护自己，tree2维护自己乘i
void update(ll p,ll x){
	ll M=p;
	while (p<=n){
		tree1[p]+=x,tree2[p]+=x*M;
		p+=lowbit(p);
	}
}

ll query(ll x){
	ll cnt=0,M=x;
	while (x>0){
		cnt+=(M+1)*tree1[x]-tree2[x];
		x-=lowbit(x);
	}
	return cnt;
}

不过呢，总感觉没啥用，因为结合律的限制，很多操作都不能进行，虽然码量较小，但是综合评价，不如线段树。

例题

例题1——求逆序对

洛谷——求逆序对

首先，我们要跳出一个思维，就是树状数组只能解决区间类问题的这个局限性，我们要明白，只要是符合结合律的都可以使用树状数组，那么我们怎么思考呢？我们要回到逆序对的定义，什么是逆序对？是不是在 \(i\) 的前面，并且大于 \(a[i]\)，那么我们就直接用树状数组动态维护比当前值的要大的，并且在当前值前面的不就可以了吗？

#include<bits/stdc++.h>
using namespace std;

const int INF=1e5+10;
int a[INF],tree[INF];
long long ans;

int lowbit(int x){
	return x&(-x);
}

void update(int x){
	while (x<=100005){
		tree[x]++;
		x+=lowbit(x); 
	}
}

long long query(int x){
	long long cnt=0;
	while (x>=1){
		cnt+=tree[x];
		x-=lowbit(x);
	}
	return cnt;
}

int main(){
	int n;
	cin>>n;
	for (int i=1;i<=n;i++){
		cin>>a[i];
	}
	for (int i=n;i>=1;i--){
		update(a[i]);
		ans+=query(a[i]-1);
	}
	cout<<ans;
	return 0;
}

例题2——三元上升子序列

洛谷——三元上升子序列

这道题还是是比较裸的，只需要维护出当前这个点之前的比他小的，同时维护出后面比他大的，然后把二者的数量相乘，就得到了一个点的答案，然后求和就行了。

#include<bits/stdc++.h>
using namespace std;
const int INF=3e5+10;

int a[INF],b[INF],n;
int tree1[INF],tree2[INF],ans1[INF],ans2[INF];
long long ans;
map<int,int> mp;

int lowbit(int x){
	return x&(-x);
}

void disc(){
	sort(b+1,b+1+n);
	int num=0;
	for (int i=1;i<=n;i++){
		if (b[i]!=b[i-1])num++,mp[b[i]]=num;
	}
	for (int i=1;i<=n;i++){
		a[i]=mp[a[i]];
	}
}

void update1(int p,int x){
	while (p<=n){
		tree1[p]+=x;
		p+=lowbit(p);
	}
}

int query1(int x){
	int cnt=0;
	while (x>0){
		cnt+=tree1[x];
		x-=lowbit(x);
	}
	return cnt;
}

void update2(int p,int x){
	while (p<=n){
		tree2[p]+=x;
		p+=lowbit(p);
	}
}

int query2(int x){
	int cnt=0;
	while (x>0){
		cnt+=tree2[x];
		x-=lowbit(x);
	}
	return cnt;
}
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n;
	for (int i=1;i<=n;i++)cin>>a[i],b[i]=a[i];
	disc();
	for (int i=1;i<=n;i++){
		update1(a[i],1);
		ans1[i]=query1(a[i]-1);
	}
	for (int i=n;i>=1;i--){
		update2(a[i],1);
		ans2[i]=(n-i+1)-query2(a[i]);
	}
	for (int i=1;i<=n;i++){
		ans+=1ll*ans1[i]*ans2[i];
	}
	cout<<ans;
	return 0;
}

例题3——校门外的树

一本通——校门外的树

这道题我们会注意到一点特殊的，那就是每一次所种的树是不同的，这就使我们可以用树状数组去做，否则的话，我们就要使用特殊的线段树或者主席树来做了。

假设一段区间的左端点为左括号，右端点为右括号，然后看一段区间内的树的种类和括号数量的关系就可以了。

#include<bits/stdc++.h>
using namespace std;
const int INF=5e4+10;

int tree[INF][2];//0->left,1->right
int n,m;

inline int lowbit(int x){
	return x&(-x);
}

void update(int p,int x){
	while (p<=n){
		tree[p][x]++;
		p+=lowbit(p);
	}	
}

int query(int p,int x){
	int cnt=0;
	while (p>0){
		cnt+=tree[p][x];
		p-=lowbit(p);
	}
	return cnt;
}
int main(){
	cin>>n>>m;
	for (int i=1;i<=m;i++){
		int k,l,r;
		cin>>k>>l>>r;
		if (k==1){
			update(l,0);
			update(r,1);
		}else {
			cout<<query(r,0)-query(l-1,1)<<endl;
		}
	}
	return 0;
}

例题4——数星星

一本通——数星星

这道题我们还是要转换思路。首先，如果说我们把所有 \(x\) 相等的数放在一起，然后按 \(y\) 从小到大排序，那么整个图是不是就是有序的？那么我在从右向左的过程中，动态查询小于等于当前 \(y\) 的个数，然后再累加起来，是不是就可以了？

#include<bits/stdc++.h>
using namespace std;
#define endl "\n"
const int INF=32010;
struct Node{
	int x,y;
}a[INF];

bool cmp(const Node a1,const Node a2){
	return a1.x==a2.x?a1.y<a2.y:a1.x<a2.x;
}
int n,maxn,col[INF],tree[INF];

inline int lowbit(int x){
	return x&(-x);
}

inline void update(int p){
	while (p<=maxn){
		tree[p]++;
		p+=lowbit(p);
	}
}

inline int query(int p){
	int cnt=0;
	while (p>0){
		cnt+=tree[p];
		p-=lowbit(p);
	}
	return cnt;
}

int main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n;
	for (int i=1;i<=n;i++){
		cin>>a[i].x>>a[i].y;
		a[i].x++,a[i].y++;
		maxn=max(maxn,a[i].y);	
	}
	sort(a+1,a+1+n,cmp);
	for (int i=1;i<=n;i++){
		int num=query(a[i].y);
		col[num]++;
		update(a[i].y);
	}
	for (int i=0;i<n;i++){
		cout<<col[i]<<endl;
	}
	return 0;
}
posted @ 2025-06-28 21:10  CylMK  阅读(60)  评论(0)    收藏  举报