浅说并查集
简单并查集
作为OI中最为优雅的数据结构,常常被大家拿来赞赏,尽管他的用处不多,但是还是很有必要讲一讲的。
小引
并查集作为一种用于管理元素所属集合的数据结构,他的本质其实就是维护出多棵树,组成一个森林,而其中的每一棵树就是代表的一个集合,而这个树上的的点就代表对应集合中的元素。
既然并查集的本质是树,那么它很显然可以做到两种简单的操作: \(Union\),\(Find\)。
-
\(Unoin\):合并两个元素他们所在的集合(换句话说就是合并两个树)
-
\(Find\):查询某个元素所在的集合(换句话说就是问这个元素在那个树中)
那么我们要怎么实现这两个操作呢?
我们先考虑如何判断两个元素是否在同一集合中。
假设我们对每棵树都编一个号,然后设 \(fa[i]\) 表示 \(i\) 号在 \(fa[i]\) 这个集合中,如果说 \(fa[i]==fa[j]\) 是不是就可以说明 \(i\) 和 \(j\) 在同一集合中了?
那么现在的问题就转化成了如何维护这个 \(fa\)。假如说现在我们要让 \(i\) 所在的集合和 \(j\) 所在的集合合并起来,我们可以怎么做?是不是可以让 \(fa[i]=fa[j]\)?显然是错误的!!为啥?因为 \(i\) 所在的集合不只是有 \(i\),除此之外还有其他的元素,那么这些元素也要改!所以说我们还不如直接暴力改,这样改一次的时间复杂度是 \(\cal O(n)\) 的,那么总共的时间复杂度就是 \(\cal O(n^2)\) 的。
那么还能不能更快一些呢?答案是可以的。
因为我们的每一个集合本质上是用一棵在存储,所以说当一个集合和另一个集合要合并的时候,我们只需要把一棵树的根节点甩到另一个树的根节点的儿子节点就行。
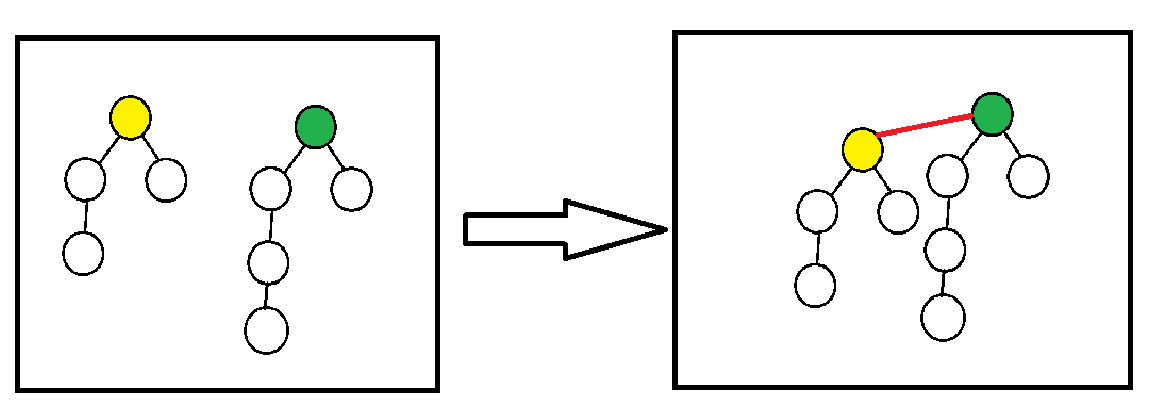
那么此时就是说,对于查询的某一个点,我们就应该一直向上查询,直到查询到真正的根节点为止。那么什么样的点才有资格被评为根节点呢?
如果说我们设刚开始每个点的 \(fa\) 都等于自己,也就是说 \(fa[i]=i\),那么很显然,当一个点满足 \(fa[i]=i\) 这个条件的时候,他就是一个真正的根节点!
所以说现在的操作就变成了,找到 \(i\) 和 \(j\) 所在集合的根节点 \(root_i\ root_j\),然后将 \(fa[root_i]=root_j\) 这样是不是就可以了?而且对于下一次找寻的时候,也会找到新的根节点,所以说这样就又可以完成这个操作了!
只不过这里要关注一个点,为了保证时间复杂度降低,我们每一次查询的时候都会更新这个点的根节点,以避免多次查询的时候反复跑路径,从而导致时间复杂度很高。
为什么所这这样的操作方法时间复杂度很低呢?我们可以大致感受一下。
比如说当前的一棵树的深度已经为 \(n-1\) 了,而且树上的最下面的节点是从来没有被更新过的,现在恰好选择了这个节点和最后的一个节点结合,那么在这样的情况下这个点需要跑 \(n-1\) 这么长的路径,同时之前为了把这个树给合并起来,起码也要花 \(n\) 的时间,那么这样算下来的话,总时间复杂度就是 \(\cal O(2\times n)\),均摊到每一次的话,差不多就是一个常数的大小,所以说时间复杂度是真的非常的低的。
-
\(Union\) 模板
void merge(int x,int y){ fa[find(x)]=find(y); } -
\(Find\) 模板
int find(int x){ if (fa[x]==x)return x; else { fa[x]=find(fa[x]); return fa[x]; } } -
初始化模板
for (int i=1;i<=n;i++){ fa[i]=i; }
例题1——亲戚
这个就是一个非常裸的并查集模板,可以直接套用。
#include<bits/stdc++.h>
using namespace std;
const int INF=1e6+10;
int fa[INF];
inline int read(){
bool b=false;
int x=0;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-')b=true;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+ch-'0';
ch=getchar();
}
return b?-x:x;
}
int find(int x){
if (fa[x]==x)return x;
else {
fa[x]=find(fa[x]);
return fa[x];
}
}
void merge(int x,int y){
fa[find(x)]=find(y);
}
int main(){
int n=read(),m=read(),q;
for (int i=1;i<=n;i++){
fa[i]=i;
}
for (int i=1;i<=m;i++){
int u=read(),v=read();
merge(u,v);
}
q=read();
for (int i=1;i<=q;i++){
int u=read(),v=read();
if (find(u)==find(v))puts("Yes");
else puts("No");
}
return 0;
}
例题2——奶酪
这道题也算是一个并查集的应用类的题目,首先我们知道如果两个球形圆洞相切或相交的话,这两个之间就是可以联通的对吧,那么如果说我们把这两个放到一个集合中,然后依次类推,我们就可以得到整块奶酪中的联通情况对吧,现在我们是不是只需要枚举最上层和最下层的空洞的坐标,看看能不能联通不就完了?
#include<bits/stdc++.h>
using namespace std;
const int INF=1100;
int fa[INF],up[INF],down[INF];
long long X[INF],Y[INF],Z[INF];
long long dis(long long x,long long y,long long z,long long x1,long long y1,long long z1){
return (x-x1)*(x-x1)+(y-y1)*(y-y1)+(z-z1)*(z-z1);
}
int find(int x){
if (fa[x]==x)return x;
else {
fa[x]=find(fa[x]);
return fa[x];
}
}
void merge(int x,int y){
fa[find(x)]=find(y);
}
int main(){
int T;
cin>>T;
while (T--){
int n,h,r,cnt1=0,cnt2=0;
cin>>n>>h>>r;
for (int i=1;i<=n;i++){
fa[i]=i;
}
for (int i=1;i<=n;i++){
cin>>X[i]>>Y[i]>>Z[i];
if (Z[i]+r>=h){//最上层
up[++cnt1]=i;
}
if (Z[i]-r<=0){//最下层
down[++cnt2]=i;
}
for (int j=1;j<=i;j++){
if (dis(X[i],Y[i],Z[i],X[j],Y[j],Z[j])<=4ll*r*r){//判断是否能联通
merge(i,j);
}
}
}
bool flag=0;
for (int i=1;i<=cnt1;i++){
for (int j=1;j<=cnt2;j++){
if (find(up[i])==find(down[j])){//暴力枚举加判断
flag=1;
break;
}
}
if (flag)break;
}
if (flag)cout<<"Yes\n";
else cout<<"No\n";
}
return 0;
}
并查集判环
很显然我们是可以把两个联通的点放入一个集合中的,而当我们发现有两个点已经再同一个集合中的时候,就说明这个图是有环的了。下面是一个例子:
问题:判断无向图
{{0,1}, {1,2}, {2,0}}是否有环。步骤:
- 初始化:每个节点的父节点是自己(
parent=[0,1,2])。- 处理边 (0,1):合并 0 和 1,
parent[0]=1。- 处理边 (1,2):合并 1 和 2,
parent[2]=1。- 处理边 (2,0):
- 查找 2 的根:
1。- 查找 0 的根:
1。- 根相同,存在环!
而这个的代码也是非常好写的,如下:
cin>>u>>v;
if (fa[find(u)]==fa[find(v)]){
cout<<"Found";
break;
}else merge(u,v);
当然这个环也不一定真的是图上的环,可能是一些存在循环的情况。
例题3——程序自动分析
这道题也是比较简单的,很容易想到,我们可以先把所有由等于符号连接的两个点放到一个并查集中,然后再去判断由不等号连接的两个是不是再一个图中,如果在,那么就说明不成立,如果不在就说明成立。只不过这道题要离散化一下,因为 \(i,j\) 太大了。当然,也可以直接用 \(map\)。
#include<bits/stdc++.h>
using namespace std;
const int INF=2e6+10;
struct Node{
int u,v,e;
}a[INF];
int fa[INF],cnt;
inline int read(){
int x=0,f=1;char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
return x*f;
}
int find(int x){
if (fa[x]!=x)fa[x]=find(fa[x]);
return fa[x];
}
void merge(int u,int v){
int tx=find(u),ty=find(v);
if (tx!=ty)fa[find(u)]=find(v);
}
unordered_map<int,int>mp;
int main(){
int T=read();
while (T--){
int n;
cin>>n;
for (int i=1;i<=n;i++){
a[i].u=read(),a[i].v=read(),a[i].e=read();
if (mp[a[i].u]==0)mp[a[i].u]=++cnt,a[i].u=cnt;//映射
else a[i].u=mp[a[i].u];
if (mp[a[i].v]==0)mp[a[i].v]=++cnt,a[i].v=cnt;
else a[i].v=mp[a[i].v];
}
for (int i=1;i<=cnt;i++)fa[i]=i;
for (int i=1;i<=n;i++){
if (a[i].e==1)merge(a[i].u,a[i].v);
}
bool flag=true;
for (int i=1;i<=n;i++){
if (a[i].e==0){
int tx=find(a[i].u),ty=find(a[i].v);
if (tx==ty){
puts("NO");
flag=0;
break;
}
}
}
if (flag)puts("YES");
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号