P4192 旅行规划

P4192 旅行规划

题目描述

OIVillage 是一个风景秀美的乡村，为了更好的利用当地的旅游资源，吸引游客，推动经济发展，xkszltl 决定修建了一条铁路将当地 \(n\) 个最著名的景点连接起来，让游客可以通过火车从铁路起点（1 号景点）出发，依次游览每个景区。为了更好的评价这条铁路，xkszltl 为每一个景区都赋予了一个美观度，而一条旅行路径的价值就是它所经过的景区的美观度之和。不过，随着天气与季节的变化，某些景点的美观度也会发生变化。

xkszltl 希望为每位旅客提供最佳的旅行指导，但是由于游客的时间有限，不一定能游览全部景区，然而他们也不希望旅途过于短暂，所以每个游客都希望能在某一个区间内的车站结束旅程，而 xkszltl 的任务就是为他们选择一个终点使得旅行线路的价值最大。可是当地的景点与前来观光的旅客实在是太多了，xkszltl 无法及时完成任务，于是找到了准备虐杀 NOI2011 的你，希望你能帮助他完成这个艰巨的任务。

输入格式

第一行给出一个整数 \(n\)，接下来一行给出 \(n\) 个景区的初始美观度。

第三行给出一个整数 \(m\)，接下来 \(m\) 行每行为一条指令：

1. 0 x y k：表示将 \(x\) 到 \(y\) 这段铁路边上的景区的美观度加上k；

2. 1 x y：表示有一名旅客想要在 \(x\) 到 \(y\) 这段（含 \(x\) 与 \(y\)）中的某一站下车，你需要告诉他最大的旅行价值。

输出格式

对于每个询问，输出一个整数表示最大的旅行价值。

说明/提示

\(n,m \leq 100000\)。

Solution:

我们先分析题目：我们维护一下前缀和数组 \(sum_i\)，每次修改对一个区间 \([l,r]\) 的 \(sum_i\) 的影响是形如一个一次函数的，而对后面的 \([r+1,n]\) 的影响是固定的 \((r-l+1)\times k\)

我们发现虽然“维护一次函数”听起来很像李超树，但是认真学过李超树的人都会发现这是完全不一样的，李超树维护的是“插入线段，单点求最值”。在本题中完全不适用。所以我们很难使用数据结构去快速的统计贡献。

那么我们考虑优秀一点的暴力：我们不难发现，一次修改对于 \([r+1,n]\) 的贡献是确定的，这很像分块时我们给一个块打上区间加法标记。所以我们考虑分块，对于散块我们暴力重构就好了。

接下来处理整块：

对于所有处在 \([l,r]\) 区间的整块：

• 我们有转移 \(sum_i \rightarrow sum_i+kx+b\) 然后我们只关心这次转移之后区间的最大值。

• 然后我们发现，对于同个区间 \(b\) 都是一样的，所以我们考虑最后再加，现在问题变成了对于一个块 \(x\)，快速求出 \(\max\limits_{i\in[l_x,r_x]}(sum_i+k\times i)\)

我们构造一个函数 \(y=k\times i+(sum_i+k\times i)\)

我们带入 \(x=-i\) 会发现：
\(y=-ki+ki+sum_i=sum_i\)
即该函数过点 \((-i,sum_i)\)，且该函数的与 \(y\) 轴截距为我们的所求。

我们画个图：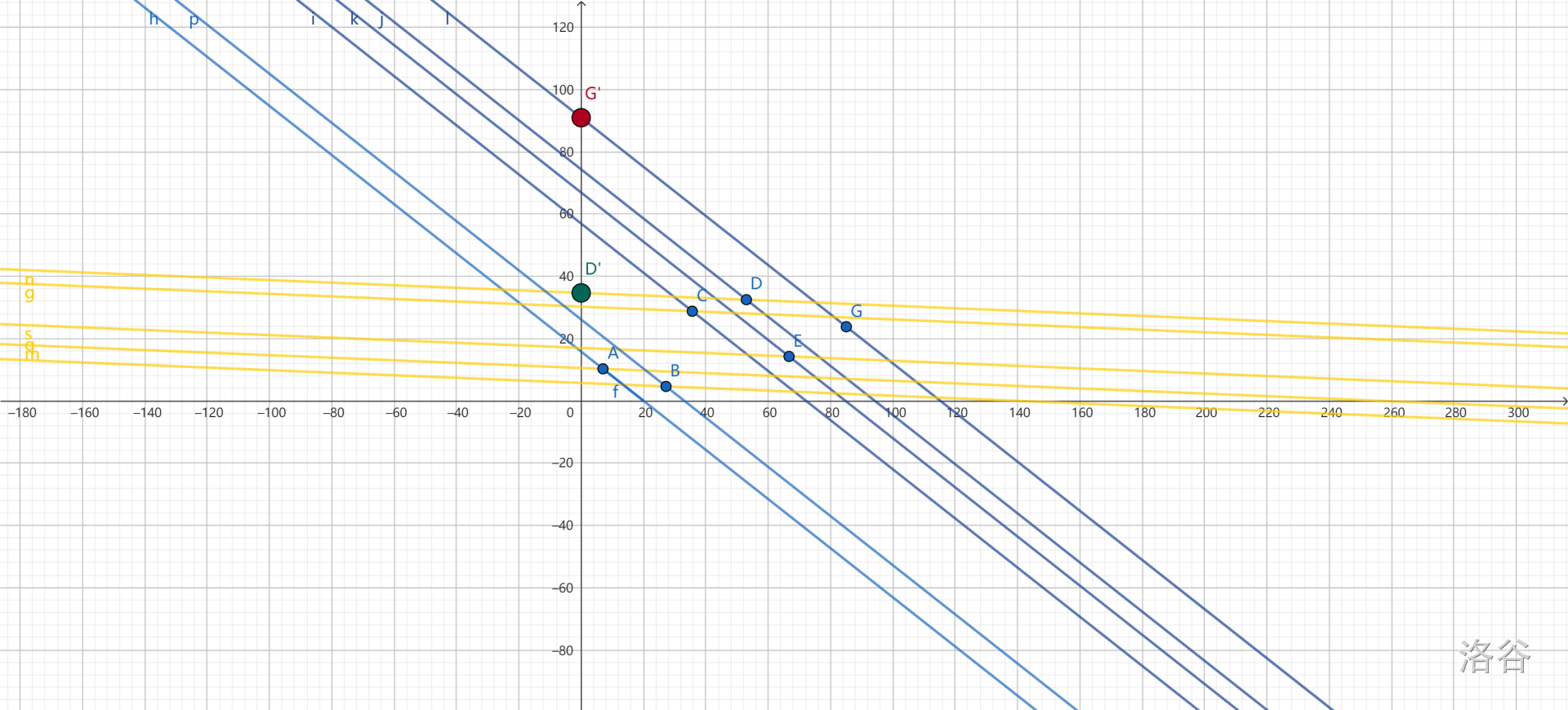
注意，为了便于观察，这里我将直线的斜率 \(k\) 和自变量 \(x\) 都取了相反数，但不难发现截距还是不变的。

黄线，蓝线分别代表两次不同的更新， \(D',G'\) 分别代表这次更新后最高的截距由 \(D,G\) 分别取到。

然后我们不难发现一些事情，如果我们对于更新的线作一条垂线然后把这两条互相垂直的线段当成坐标轴来看，那么我们每次取到的点就恰好是这个新坐标系中最高的点：

然后我们还发现一些点对于任意直线都是没有贡献的，比如点 \(B\)。如果我们对于这些点维护一个上凸壳，真正有可能产生贡献的点其实是凸壳上的点。

那么我们现在的问题就是在这个凸壳上求一个坐标系被旋转了 \(arctan(k)\) 之后最高的点，然后凸壳有个很好的性质就是凸壳被任意旋转之后仍然是凸壳，那么我们要找的“最高点”实际上是这个单波峰凸壳上的那个波峰，所以我们直接二分就好了。

然后补充说明一下，我们的原题是将区间所有的点全部加上一个等差数列，但是上面我只说了加上一个等差数列的情况，这个做法是不是假了。其实没有，因为两个等差数列的和仍旧是一个等差数列。

时间复杂度：

单次更新的代价是 \(O(\sqrt n)\),询问有一个块内二分 \(O(\sqrt n\times \log{\sqrt n})\)
由于 \(\log{\sqrt n}\) 实在太小，而且更新的常数不小，所以几乎认为他们的代价相同，块长取 \(B=\sqrt n\) 时间复杂度来到一个常数比较大的 \(O(m\sqrt m)\)

然后这题就做完了。

Code:

#include<bits/stdc++.h>
#define int long long
#define Max(x,y) (x > y ? x : y)
#define Min(x,y) (x < y ? x : y)
using namespace std;
const int N=1e5+5;
const int Len=335;
const int inf=1e17;
int n,m,cnt,len,tp;
int a[N],siz[N];
int sta[N],conv[Len][Len];
int l[N],r[N],bl[N];
int k[N],b[N],add[N];//y=kx+b
inline double K(int x,int y)
{
    return (double)((a[x]-a[y])/(x-y));
}
void build_conv(int x)
{
    sta[tp=1]=l[x];
    for(int i=l[x]+1;i<=r[x];i++)
    {
        while(tp>=2&&(K(sta[tp-1],sta[tp])<K(sta[tp-1],i)))tp--;
        sta[++tp]=i;
    }
    siz[x]=tp;sta[0]=0,sta[++tp]=n+1;
    for(int i=0;i<=tp;i++)conv[x][i]=sta[i];
}
void build()
{
    len=sqrt(n);
    cnt=n/len+(n%len!=0);
    for(int i=1;i<=n;i++)bl[i]=(i-1)/len+1;
    for(int i=1;i<=cnt;i++)l[i]=(i-1)*len+1,r[i]=i*len;r[cnt]=n;
    for(int i=1;i<=cnt;i++)build_conv(i);
}
void pushdown(int x)
{
    int sum=0;
    for(int i=l[x];i<=r[x];i++)
    {
        a[i]+=sum+b[x]+add[x];
        sum+=k[x];
    }
    k[x]=b[x]=add[x]=0;
}
int val(int x)
{
    if(!x||x==n+1)return -inf;
    return a[x]+b[bl[x]]+add[bl[x]]+k[bl[x]]*(x-l[bl[x]]);
}
void upd(int ll,int rr,int w)
{
    int sum=0;
    if(bl[ll]==bl[rr])
    {
        pushdown(bl[ll]);
        for(int i=ll;i<=rr;i++)sum+=w,a[i]+=sum;
        for(int i=rr+1;i<=r[bl[rr]];i++)a[i]+=sum;
        for(int i=bl[rr]+1;i<=cnt;i++)add[i]+=sum;
        build_conv(bl[rr]);
        return;
    }
    sum=w*(r[bl[ll]]-ll+2);
    for(int i=bl[ll]+1;i<bl[rr];i++)
    {
        b[i]+=sum;k[i]+=w;
        sum+=len*w;
    }
    // 左散块
    pushdown(bl[ll]);sum=0;
    for(int i=ll;i<=r[bl[ll]];i++)sum+=w,a[i]+=sum;
    build_conv(bl[ll]);
    // 右散块
    pushdown(bl[rr]);sum=w*(l[bl[rr]]-ll);
    for(int i=l[bl[rr]];i<=rr;i++)sum+=w,a[i]+=sum;
    for(int i=rr+1;i<=r[bl[rr]];i++)a[i]+=sum;
    build_conv(bl[rr]);
    for(int i=bl[rr]+1;i<=cnt;i++)add[i]+=sum;
    // 后续节点的前缀和
    return;
}
int find(int x)
{
    int ll=1,rr=siz[x],mid,k1,k2,k3;
    while(ll<=rr)
    {
        mid=ll+rr>>1;
        k1=val(conv[x][mid-1]);k2=val(conv[x][mid]);k3=val(conv[x][mid+1]);
        if(k1>k2&&k2>k3)rr=mid-1;
        else if(k1<k2&&k2<k3)ll=mid+1;
        else return k2;
    }
}
int query(int ll,int rr)
{
    int ans=-inf;
    if(bl[ll]==bl[rr])
    {
        for(int i=ll;i<=rr;i++)ans=Max(ans,val(i));
        return ans;
    }
    for(int i=ll;i<=r[bl[ll]];i++)ans=Max(ans,val(i));
    for(int i=l[bl[rr]];i<=rr;i++)ans=Max(ans,val(i));
    for(int i=bl[ll]+1;i<bl[rr];i++)ans=Max(ans,find(i));
    return ans;
}
void work()
{
    cin>>n;
    for(int i=1;i<=n;i++)scanf("%lld",&a[i]),a[i]+=a[i-1];
    a[0]=a[n+1]=-inf;build();
    cin>>m;
    for(int i=1,opt,ll,rr,w;i<=m;i++)
    {
        scanf("%lld",&opt); scanf("%lld%lld",&ll,&rr);
        if(!opt)
        {
           scanf("%lld",&w);
            upd(ll,rr,w);
        }
        else
        {
            int ans=query(ll,rr);
            printf("%lld\n",ans);
        }
    }
}
#undef int
int main()
{
    //freopen("P4192.in","r",stdin);
    //freopen("P4192.out","w",stdout);
    work();
    return 0;
}