P6645 [CCO 2020] Interval Collection

题目背景

本题题面来自 LOJ。

题目描述

Altina 正进行区间收藏。一对满足 \(l < r\) 的正整数 \([l, r]\) 为一个区间，我们称这样的区间的长度为 \(r - l\)。

我们称区间 \([l, r]\) 包含区间 \([x, y]\)，当且仅当 \(l \le x\) 并且 \(y \le r\)。特别地，每个区间都包含自身。

定义一个非空集合 \(S\) 的最大公共子区间为被 \(S\) 中每个区间都包含的区间中最长的那个，如果没有这样的区间则未定义。

定义一个非空集合 \(S\) 的最小公共超区间为包含 \(S\) 中每个区间的区间中最短的那个，注意这样的区间总是存在。

初始时，Altina 的收藏中没有任何区间。接下来会发生 \(Q\) 个事件，对 Altina 的收藏产生改变。

Altina 往她的收藏中添加一个区间 \([l, r]\)，如果此时收藏中已有 \([l, r]\)，应该被算作不同的两个区间。
Altina 移除一个在收藏中已经存在的区间 \([l, r]\)，如有多个只以移除恰好一个。

在每个事件发生后，Altina 选择一个她的收藏中的非空子集 \(S\)，并且满足如下条件：

在所有的选取方案中，她会选择最大公共子区间未定义的。如果不存在这样的方案，则她会选择最大公共子区间的长度最小的。
在所有的满足上述条件的集合 \(S\) 中，她会选择最小公共超区间的长度最小的。

请你在每一个事件发生后，输出 Altina 会选择的集合 \(S\) 的最小公共超区间的长度。

输入格式

第一行一个正整数 \(Q\)，表示将会发生的事件的个数。
接下来 \(Q\) 行，每行描述一个事件，格式如下：

\(\mathtt{A}\;l\;r\)：添加一个区间 \([l, r]\) 到 Altina 的收藏中。
\(\mathtt{R}\;l\;r\)：从 Altina 的收藏中移除一个区间 \([l, r]\)，保证这个区间在她的收藏中存在，且移除后她的收藏非空。

输出格式

输出 \(Q\) 行，每行一个正整数表示每个事件发生后 Altina 会选择的集合 \(S\) 的最小公共超区间的长度。

子任务

本题使用捆绑测试

对于 \(100\%\) 的数据，保证 \(1\le Q\le 5\times 10^5\)，\(1\le l,r\le 10^6\)。

说明

本题译自 Canadian Computing Olympiad 2020 Day 2 T2 Interval Collection。

Solution:

为了方便描述，记 \(n=Q\)，\(l,r \le val\)

我们不难发现，选两个以上的区间是无意义的。

假设现在选了两个区间，如果再选第三个区间，那么他们的最小公共超区间的长度是不会下降的。

所以问题就转化为了：在　\(S\) 中选两个集合，最小化他们的交集的前提下最小化他们的最小公共超区间（注意不是并集）。

我们分两种情况讨论：

当集合中任意两个区间都有交时，我们记 \(L_{max},R_{min}\) 分别对应左端点的最大值和右端点的最小值。记所有以 \(L_{max}\) 为左端点的区间中右端点的最小值 \(r\) ，所有以 \(R_{min}\) 为右端点的区间中左端点的最小值 \(l\) 。
此时的最小公共超区间就是 \([l,r]\).

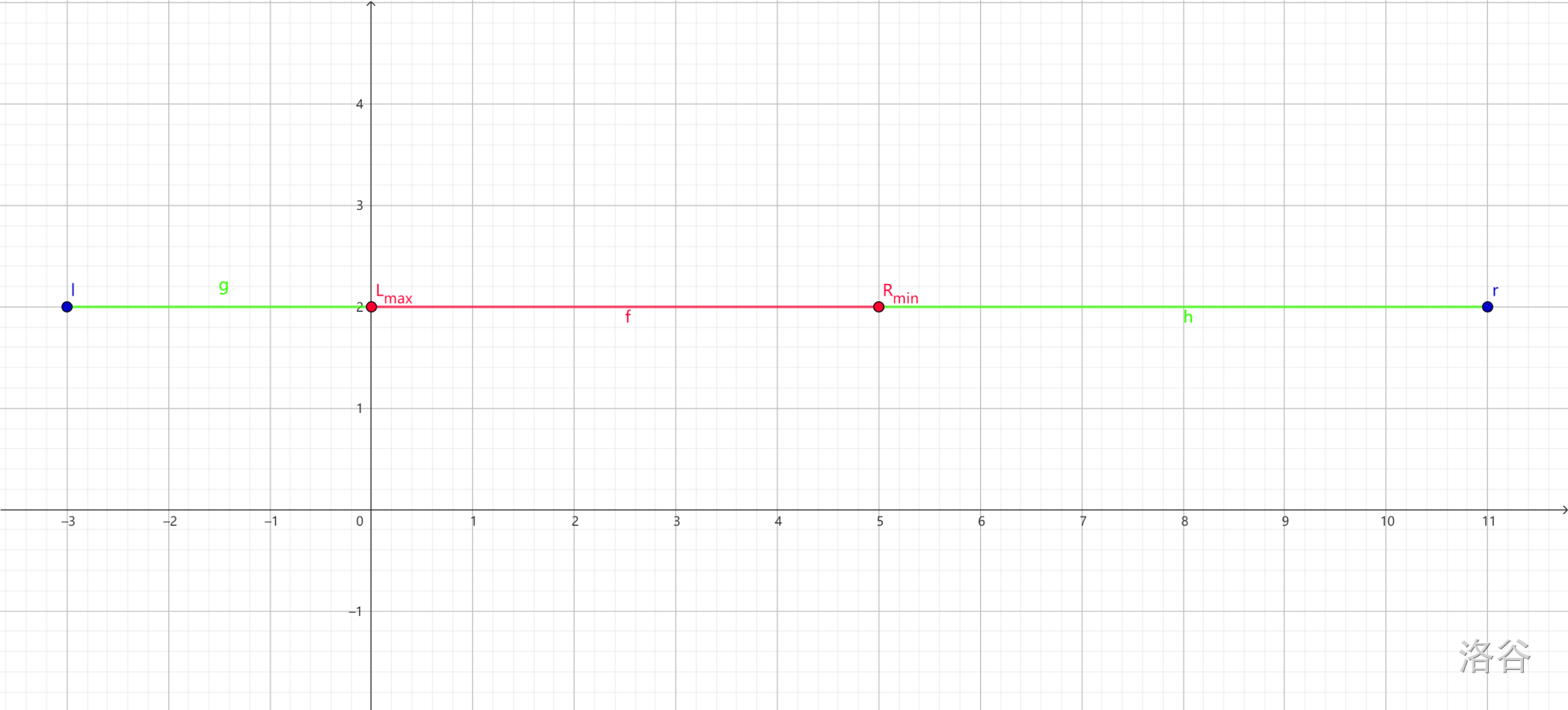
在图上就像这样，图中红色区域是交集，\(r-l\) 即为所求。

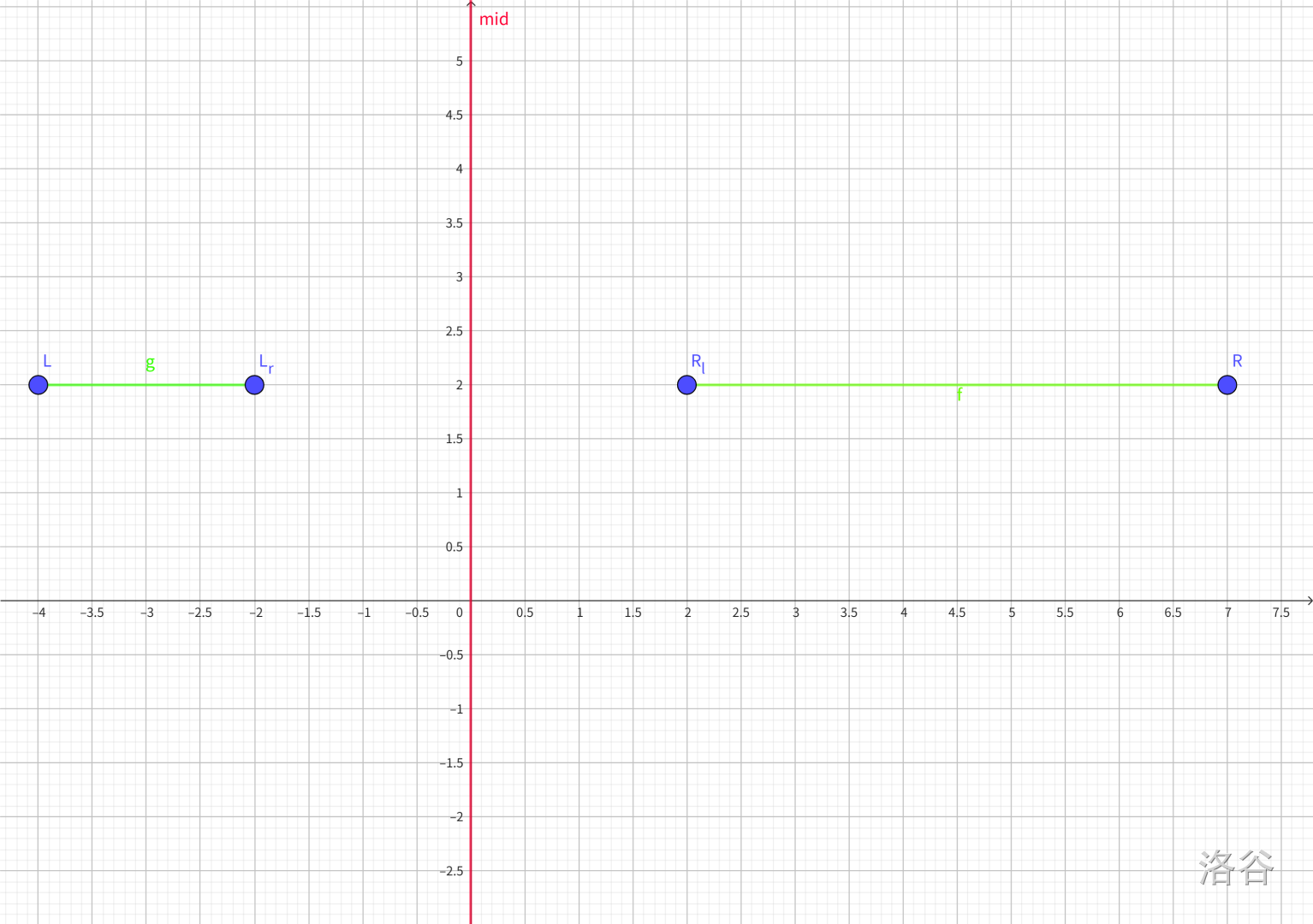
然后是集合中存在两区间无交：
我们先思考，如果我们能枚举一个分割点 \(mid\), 然后维护右端点落在 \([1,mid]\) 上的左端点最小值 \(l\)，和左端点落在 \([mid+1,val]\) 上的右端点最大值 \(r\).此时的答案即为 \(ans_{mid}=r-l\). 只要我们将所有的 \(mid\) 遍历，便能在单次 \(O(val\log n)\) 的时间复杂度下求出答案了。但是这样全局的复杂度是 \(O(n\times val\times \log n)\) 的，十分难以接受。
我们考虑优化枚举 \(mid\) 这一过程：我们在线段树上进行决策，线段树的每个节点记录 \(lp,rp,ans\). 分别表示：
右端点落在区间内时的左端点最大值 \(lp\)，左端点落在区间内时的右端点最小值 \(rp\)，决策点落在区间内的答案 \(ans\).
那么我们就可以在线段树上进行决策：对于每个线段树节点，左儿子的 \(ans\) 就表示 \(l,mid,r\) 全部落在左儿子上的答案，右儿子同理。然后我们新增一种转移：\(ans \leftarrow rson.rp-lson.lp\). 这个转移的意义就是 \(l\) 落在左儿子，\(r\) 落在右儿子。这样我们就做到了将小区间合并到大区间上。

pushup部分代码:


    inline void pushup(int x)
    {
        t[x].rp=Min(t[ls].rp,t[rs].rp);//左端点落在区间上的右端点最小值
        t[x].lp=Min(t[ls].lp,t[rs].lp);//右端点落在区间上的左端点最大值
        t[x].ans=Min(Min(t[ls].ans,t[rs].ans),t[rs].rp+t[ls].lp);
    }

注意这里我维护的 \(lp\) 是已经取了相反数的，所以是取 \(Min\) 然后相加，其实维护的是真实值的最大值。

然后就是对于每个节点 \(i\) 我们需要维护一个数据结构来动态的查询以这个节点为左端点的区间中，其对应的右端点的最小值。我使用了两个 priority_queue 来实现一个可删除的优先队列，具体实现见代码。

Code:

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
const int inf=1e9;
#define Max(x,y) (x>y? x:y)
#define Min(x,y) (x<y? x:y)
//int Max(int x,int y){return x>y ? x : y;}
//int Min(int x,int y){return x<y ? x : y;}
struct Seg{
    #define ls (x<<1)
    #define rs (x<<1|1)
    #define mid (l+r>>1)
    struct tree{
        int mx,tag;
    }t[N<<2];
    inline void add(int x,int k){t[x].tag+=k,t[x].mx+=k;}
    inline void pushdown(int x)
    {
        if(!t[x].tag)return;
        add(ls,t[x].tag),add(rs,t[x].tag);
        t[x].tag=0;
    }
    inline void pushup(int x)
    {
        t[x].mx=Max(t[ls].mx,t[rs].mx);
    }
    inline void upd(int x,int l,int r,int L,int R,int k)
    {
        if(L<=l&&r<=R){add(x,k);return;}
        pushdown(x);if(L<=mid)upd(ls,l,mid,L,R,k);
        if(mid<R)upd(rs,mid+1,r,L,R,k);pushup(x);
    }
    #undef ls
    #undef rs
    #undef mid
}tt;
int calc=0;
struct Segment_Tree{
    #define ls (x<<1)
    #define rs (x<<1|1)
    #define mid (l+r>>1)
    struct tree{
        int rp,lp,ans;
    }t[N<<2];
    inline void pushup(int x)
    {
        t[x].rp=Min(t[ls].rp,t[rs].rp);//左端点落在区间以右的右端点最小值
        t[x].lp=Min(t[ls].lp,t[rs].lp);//右端点落在区间以左的左端点最大值
        t[x].ans=Min(Min(t[ls].ans,t[rs].ans),t[rs].rp+t[ls].lp);
    }
    inline void build(int x,int l,int r)
    {
        t[x]={inf,inf,inf};if(l==r)return;
        build(ls,l,mid);build(rs,mid+1,r);
    }
    inline void insl(int x,int l,int r,int pos,int k)
    {
        if(l==r){t[x].rp=k;t[x].ans=t[x].lp+t[x].rp;return;}
        if(pos<=mid)insl(ls,l,mid,pos,k);
        if(mid<pos)insl(rs,mid+1,r,pos,k);pushup(x);
    }
    inline void insr(int x,int l,int r,int pos,int k)
    {
        if(l==r){t[x].lp=k;t[x].ans=t[x].lp+t[x].rp;return;}
        if(pos<=mid)insr(ls,l,mid,pos,k);
        if(mid<pos)insr(rs,mid+1,r,pos,k);pushup(x);
    }
    #undef ls
    #undef rs
    #undef mid
}T;
int n,m,val=1e6;
struct data{
    priority_queue<int> A,E;
    void add(int x){A.push(x);}
    void del(int x){E.push(x);}
    int find(){while(!E.empty()&&A.top()==E.top()){A.pop(),E.pop();}return A.top();}
}L[N],R[N];
#define pi pair
#define mp(x,y) make_pair(x,y)
struct  Data
{
    priority_queue<pair<int,int> >A,E;
    void add(int x,int y){A.push(mp(x,y));}
    void del(int x,int y){E.push(mp(x,y));}
    int find(){while(!E.empty()&&A.top()==E.top())A.pop(),E.pop();return A.top().second;}
}LL,RR;
void work()
{
    std::ios_base::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    cin>>n;
    T.build(1,1,val);
    char c;int l,r,cnt=0;
    for(int i=1;i<=val;i++)R[i].add(-inf),L[i].add(-inf);
    for(int i=1;i<=n;i++)
    {
        cin>>c>>l>>r;
        if(c=='A')
        {
            tt.upd(1,1,val,l,r,1);cnt++;
            L[l].add(-r);T.insl(1,1,val,l,-L[l].find());
            R[r].add(l);T.insr(1,1,val,r,-R[r].find());
            LL.add(l,-r);RR.add(-r,l);
        }
        if(c=='R')
        {
            tt.upd(1,1,val,l,r,-1);cnt--;
            L[l].del(-r);T.insl(1,1,val,l,-L[l].find());
            R[r].del(l);T.insr(1,1,val,r,-R[r].find());
            LL.del(l,-r);RR.del(-r,l);
        }
        if(tt.t[1].mx==cnt)
        {
            cout<<-(LL.find()+RR.find())<<"\n";
        }
        else
        {
            cout<<T.t[1].ans<<"\n";
        }
    }
}
int main()
{
    //freopen("seq.in","r",stdin);
    //freopen("seq.out","w",stdout);
    work();
    return 0;
}

posted @ 2025-08-06 14:11 liuboom 阅读(3) 评论(0) 收藏举报

刷新页面返回顶部

LG017

喜欢数据结构捏

P6645 [CCO 2020] Interval Collection

P6645 [CCO 2020] Interval Collection

题目背景

题目描述

输入格式

输出格式

子任务

说明

Solution:

Code:

公告