P2403 [SDOI2010] 所驼门王的宝藏
P2403 [SDOI2010] 所驼门王的宝藏
题目描述
在宽广的非洲荒漠中,生活着一群勤劳勇敢的羊驼家族。被族人恭称为“先知”的 AlpacaL.Sotomon 是这个家族的领袖,外人也称其为“所驼门王”。所驼门王毕生致力于维护家族的安定与和谐,他曾亲自率军粉碎河蟹帝国主义的野蛮侵略,为族人立下赫赫战功。所驼门王一生财宝无数,但因其生性节俭低调,他将财宝埋藏在自己设计的地下宫殿里,这也是今天 Henry Curtis 故事的起点。Henry 是一个爱财如命的贪婪家伙,而又非常聪明,他费尽心机谋划了这次盗窃行动,破解重重机关后来到这座地下宫殿前。
整座宫殿呈矩阵状,由 \(R \times C\) 间矩形宫室组成,其中有 \(N\) 间宫室里埋藏着宝藏,称作藏宝宫室。宫殿里外、相邻宫室间都由坚硬的实体墙阻隔,由一间宫室到达另一间只能通过所驼门王独创的移动方式——传送门。所驼门王为这 \(N\) 间藏宝宫室每间都架设了一扇传送门,没有宝藏的宫室不设传送门,所有的宫室传送门分为三种:
- “横天门”:由该门可以传送到同行的任一宫室;
- “纵寰门”:由该门可以传送到同列的任一宫室;
- “任意门”:由该门可以传送到以该门所在宫室为中心周围 \(8\) 格中任一宫室(如果目标宫室存在的话)。
深谋远虑的 Henry 当然事先就搞到了所驼门王当年的宫殿招标册,书册上详细记录了每扇传送门所属宫室及类型。而且,虽然宫殿内外相隔,但他自行准备了一种便携式传送门,可将自己传送到殿内任意一间宫室开始寻宝,并在任意一间宫室结束后传送出宫。整座宫殿只许进出一次,且便携门无法进行宫室之间的传送。不过好在宫室内传送门的使用没有次数限制,每间宫室也可以多次出入。
现在 Henry 已经打开了便携门,即将选择一间宫室进入。为得到尽多宝藏,他希望安排一条路线,使走过的不同藏宝宫室尽可能多。请你告诉 Henry 这条路线最多行经不同藏宝宫室的数目。
输入格式
第一行给出三个正整数 \(N,R,C\)。
以下 \(N\) 行,每行给出一扇传送门的信息,包含三个正整数 \(x_i,y_i,T_i\),表示该传送门设在位于第 \(x_i\) 行第 \(y_i\) 列的藏宝宫室,类型为 \(T_i\)。\(T_i\) 是一个 \(1 \sim 3\) 间的整数,\(1\) 表示可以传送到第 \(x_i\) 行任意一列的“横天门”,\(2\) 表示可以传送到任意一行第 \(y_i\) 列的“纵寰门”,\(3\) 表示可以传送到周围 \(8\) 格宫室的“任意门”。
保证 \(1 \le x_i \le R\),\(1 \le y_i \le C\),所有的传送门位置互不相同。
输出格式
输出只有一个正整数,表示你确定的路线所经过不同藏宝宫室的最大数目。
说明/提示
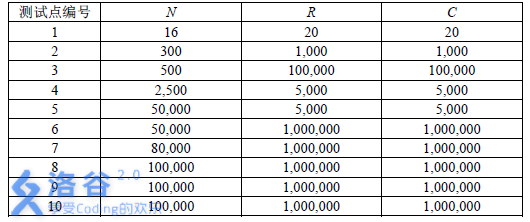
数据规模和约定:
Solution:
又是挺老的一道题,当时做的时候貌似还没降蓝,当时就觉得这玩意配紫??? 万恶的降降降
首先我们发现这题主要难在建图,我们需要在一个 $10^5 \times 10^5 $ 的图上进行寻宝,但是其实宝藏只有 \(10^5\) 级别,所以我们考虑在不同的宝藏之间连边,我们对每行每列都建一个虚点用来链接 1,2 类的传送门。对于第三种传送门,我们有非常丰富多彩的方法实现,但是当时的我想了一个十分传统的办法:二分。其实当时的实现在我现在看来是有点蠢了,但它确实是对的,我写的东西相当于将一个点 (x,y) 转化为一个 x,y 分别为第一,第二关键字的序列,然后在上面二分。如过要是现在的我写的话肯定会压成一个 \(x\times 10^5+y\) 这样的数来二分,或者直接使用 map<pair<int,int> >
但是都无所谓了,我们现在在链式前向星上建出了这幅图,我们考虑如何进行答案统计:
我们发现,我们要求的东西其实是在这个有向图上求一个最长的路径,这其实和 P3387 【模板】缩点
是完全一致的(本题相当于 P3387中所有点权均为 1 的情况)
然后这题就做完了(早期代码有点又臭又长,但是我懒得重写了,将就看吧)
#include <bits/stdc++.h>
using namespace std;
const int N=3e6+5;
int n,r,c,e_cnt,dfn_cnt,ed,scc_cnt;
int head[N];
int dfn[N],low[N],scc[N],scc_siz[N],st[N],in_st[N],f[N];
int from[N],to[N],rd[N],fa[N];
int dx[8]={-1,-1,0,1,1,1,0,-1},dy[8]={0,1,1,1,0,-1,-1,-1};
struct Edge{
int to,nxt;
}e[N<<2];
struct Node{
int x,y,opt;
}a[N];
void add(int x,int y)
{
e[++e_cnt]=(Edge){y,head[x]};
from[e_cnt]=x;to[e_cnt]=y;
head[x]=e_cnt;
}
bool cmp(Node x,Node y)
{
if(x.x!=y.x)return x.x<y.x;
return x.y<y.y;
}
int get(int x,int y)
{
int l=1,r=n;
while(l<=r)
{
int mid=l+r>>1;
if(a[mid].x==x&&a[mid].y==y)
{
return mid;
}
if(a[mid].x<x||(a[mid].x==x&&a[mid].y<y))l=mid+1;
else r=mid-1;
}
for(int i=r;i<=l;i++)
{
if(a[i].x==x&&a[i].y==y)
{
return i;
}
}
return 0;
}
void init()
{
e_cnt=0;
memset(head,0,sizeof(head));
}
void tarjan(int x)
{
dfn[x]=low[x]=++dfn_cnt;
st[++ed]=x;in_st[x]=1;
for(int i=head[x];i;i=e[i].nxt)
{
int to=e[i].to;
if(!dfn[to])
{
tarjan(to);
low[x]=min(low[x],low[to]);
}
else if(in_st[to])
{
low[x]=min(dfn[to],low[x]);
}
}
if(low[x]==dfn[x])
{
scc[x]=++scc_cnt;scc_siz[scc_cnt]=x>=r+c;
while(st[ed]!=x)
{
int now=st[ed];
scc[now]=scc_cnt;
scc_siz[scc_cnt]+=(now>r+c);
in_st[st[ed--]]=0;
}
in_st[st[ed--]]=0;
}
}
void bfs()
{
queue<int> q;
for(int i=1;i<=scc_cnt;i++)
{;
if(!rd[i])
{
q.push(i);
f[i]=scc_siz[i];
}
}
while(!q.empty())
{
int u=q.front();q.pop();
for(int i=head[u];i;i=e[i].nxt)
{
int v=e[i].to;
f[v]=max(f[v],f[u]+scc_siz[v]);
if((--rd[v])==0)
{
q.push(v);
}
}
}
}
inline void work()
{
cin>>n>>r>>c;
for(int i=1,x,y,opt;i<=n;i++)
{
scanf("%d%d%d",&x,&y,&opt);
a[i]=(Node){x,y,opt};
}
sort(a+1,a+1+n,cmp);
for(int i=1;i<=n;i++)
{
int now=r+c+i;
add(a[i].x,now);add(a[i].y+r,now);
if(a[i].opt==1){add(now,a[i].x);}
if(a[i].opt==2){add(now,a[i].y+r);}
if(a[i].opt==3)
{
for(int k=0;k<=7;k++)
{
int xx=a[i].x+dx[k],yy=a[i].y+dy[k];
if(xx<1||r<xx)continue;
if(yy<1||c<yy)continue;
int id=get(xx,yy);
if(id)
{
add(now,id+c+r);
}
}
}
}
int tot=r+c+n;
for(int i=1;i<=tot;i++)
{
if(!dfn[i])
{
tarjan(i);
}
}
queue<Edge> Q;
for(int i=1;i<=e_cnt;i++)
{
int u=from[i],v=to[i];
if(scc[u]!=scc[v])
{
Q.push((Edge){scc[u],scc[v]});
rd[scc[v]]++;
}
}
init();
while(!Q.empty())
{
int x=Q.front().to,y=Q.front().nxt;
Q.pop();
add(x,y);
}
bfs();
int ans=0;
for(int i=1;i<=scc_cnt;i++)
{
ans=max(ans,f[i]);
}
printf("%d",ans);
}
int main()
{
//freopen("a.in","r",stdin);freopen("a.out","w",stdout);
work();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号