P2046 [NOI2010] 海拔

题目描述

YT 市是一个规划良好的城市，城市被东西向和南北向的主干道划分为 \(n \times n\) 个区域。简单起见，可以将 YT 市看作 一个正方形，每一个区域也可看作一个正方形。从而，YT 城市中包括 \((n+1) \times (n+1)\) 个交叉路口和 \(2n \times (n+1)\) 条双向道路（简称道路），每条双向道路连接主干道上两个相邻的交叉路口。下图为一张 YT 市的地图（\(n = 2\)），城市被划分为 \(2 \times 2\) 个区域，包括 \(3 \times 3\) 个交叉路口和 \(12\) 条双向道路。

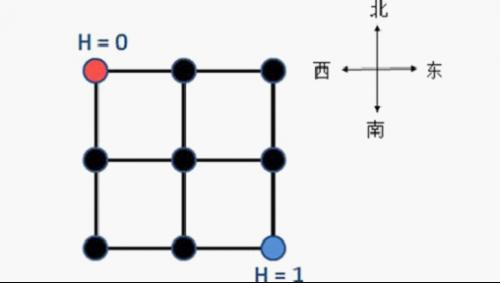
小 Z 作为该市的市长，他根据统计信息得到了每天上班高峰期间 YT 市每条道路两个方向的人流量，即在高峰期间沿着该方向通过这条道路的人数。每一个交叉路口都有不同的海拔高度值，YT 市市民认为爬坡是一件非常累的事情，每向上爬 \(h\) 的高度，就需要消耗 \(h\) 的体力。如果是下坡的话，则不需要耗费体力。因此如果一段道路的终点海拔减去起点海拔的值为 \(h\)（注意 \(h\) 可能是负数），那么一个人经过这段路所消耗的体力是 \(\max\{0, h\}\)。

小 Z 还测量得到这个城市西北角的交叉路口海拔为 \(0\)，东南角的交叉路口海拔为 \(1\)（如上图所示），但其它交叉路口的海拔高度都无法得知。小 Z 想知道在最理想的情况下（即你可以任意假设其他路口的海拔高度），每天上班高峰期间所有人爬坡消耗的总体力和的最小值。

说明/提示

数据范围

• 对于 \(80\%\) 的数据：\(n \leq 40\)；
• 对于 \(100\%\) 的数据：\(1 \leq n \leq 500\)，\(0 \leq \text{流量} \leq 10^6\) 且所有流量均为整数。

Solution：

拿到题面第一眼:这不最小割吗?
第二眼：\(n\le500\) 这不直接秒？
然后发现节点个数是 \(n^2\)
关于最小割，他死了

但我们还是说一下最小割应该这么做：

就是每个点分别向附近的点连流量为权值的边然后就跑最小割就好了。

但是我们发现点数过于大了，所以我们需要一些黑科技——对偶图。

具体文章参考:
关于平面图到对偶图的转化
对偶图对于平面图最小割的求解(网络流问题)

然后我们感性地理解一下这个结论：

“s-t的路径， 就对应了s-t的割.”

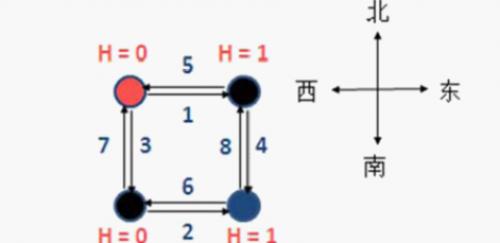
首先就是对偶中的 s,t 都是在原图的外面的，所以 s-t的路径一定横穿了原图，这就对应了割。稍微严谨一点就是你在对偶图上走的每条边在原图上对应的边都是相邻的，然后你在对偶图上走的边数右恰好等于割边的数量，所以这是一个割。那么最短路径就对应最小割了。

Code:

#include<bits/stdc++.h>
const int N=505;
const int inf=1e9;
const int M=N*N*2;
using namespace std;
int n,cnt,ans,S,T;
inline int id(int i,int j){return (i-1)*n+j;}
struct Edge{
    int to,w,nxt;
}e[M<<3|1];int head[M<<1];
void add(int x,int y,int w)
{
    e[++cnt]={y,w,head[x]};head[x]=cnt;
}
int dis[M],vis[M];
struct Node{
    int id,val;
    bool operator <(const Node &q)const{
        return q.val<val;
    }
};
priority_queue<Node> Q;
void init()
{
    for(int u=S;u<=T;u++)dis[u]=inf;
}
void dijkstra()
{
    init();dis[S]=0;Q.push({S,0});
    while(!Q.empty())
    {
        int u=Q.top().id;Q.pop();
        if(vis[u])continue;vis[u]=1;
        for(int i=head[u];i;i=e[i].nxt)
        {
            auto [v,w,id]=e[i];
            if(dis[v]>dis[u]+w)
            {
                dis[v]=dis[u]+w;
                Q.push({v,dis[v]});
            }
        }
    }
}
void work()
{
    cin>>n;n++;
    S=0,T=n*n+1;
    for(int i=1,x;i<=n;i++)for(int j=1;j<n;j++)
    {
        scanf("%d",&x);
        if(i==1)add(S,id(i,j),x);
        else if(i==n)add(id(i-1,j),T,x);
        else add(id(i-1,j),id(i,j),x);
    }
    for(int i=1,x;i<n;i++)for(int j=1;j<=n;j++)
    {
        scanf("%d",&x);
        if(j==1)add(id(i,j),T,x);
        else if(j==n)add(S,id(i,j-1),x);
        else add(id(i,j),id(i,j-1),x);
    }
    for(int i=1,x;i<=n;i++)for(int j=1;j<n;j++)
    {
        scanf("%d",&x);
        if(i==1)add(id(i,j),S,x);
        else if(i==n)add(T,id(i-1,j),x);
        else add(id(i,j),id(i-1,j),x);
    }

    for(int i=1,x;i<n;i++)for(int j=1;j<=n;j++)
    {
        scanf("%d",&x);
        if(j==1)add(T,id(i,j),x);
        else if(j==n)add(id(i,j-1),S,x);
        else add(id(i,j-1),id(i,j),x);
    }
    dijkstra();
    cout<<dis[T];
}
int main()
{
    //freopen("P2046.in","r",stdin);freopen("P2046.out","w",stdout);
    work();
    return 0;
}