P4130 [NOI2007] 项链工厂

P4130 [NOI2007] 项链工厂

题目背景

T公司是一家专门生产彩色珠子项链的公司，其生产的项链设计新颖、款式多样、价格适中，广受青年人的喜爱。

最近T公司打算推出一款项链自助生产系统，使用该系统顾客可以自行设计心目中的美丽项链。该项链自助生产系

统包括硬件系统与软件系统，软件系统与用户进行交互并控制硬件系统，硬件系统接受软件系统的命令生产指定的

项链。该系统的硬件系统已经完成，而软件系统尚未开发，T公司的人找到了正在参加全国信息学竞赛的你，你能

帮助T公司编写一个软件模拟系统吗？

题目描述

一条项链包含 \(N\) 个珠子，每个珠子的颜色是 \(1,2,…,c\) 中的一种。项链

被固定在一个平板上，平板的某个位置被标记位置 \(1\) ，按顺时针方向其他位置被记为 \(2,3,…,N\)。

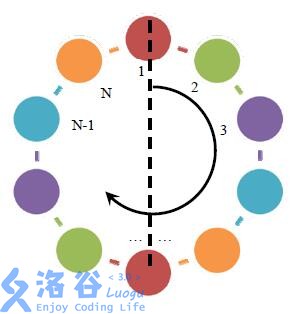
你将要编写的软件系统应支持如下命令：

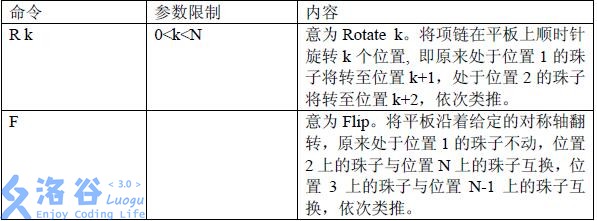
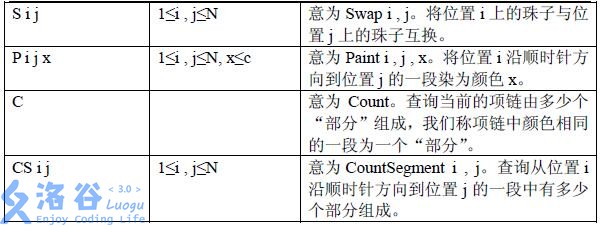
输入格式

输入文件第一行包含两个整数 \(N, c\)，分别表示项链包含的珠子数目以及颜色数目。

第二行包含 \(N\) 个整数，\(x_1, x_2…, x_n\)，表示从位置 \(1\) 到位置 \(N\) 的珠子的颜色，\(1 \le x_i \le c\)。

第三行包含一个整数 \(Q\)，表示命令数目。

接下来的 \(Q\) 行每行一条命令，如上文所述。

【数据规模和约定】

对于100%的数据，\(N \le 500000\)，\(Q \le 500000\)，\(c \le 1000\)。

Solution:

假如没有那两个怪异的旋转和折叠操作，我们可以用线段树维护颜色段轻松 AC 本题。

我们思考一下旋转和折叠的本质：

不难发现，发生折叠之后珠子间的相对位置关系是没有改变的，我们只改变了编号，并且这种改变是可以快速计算出来的：一个点 \(x\) 折叠过后的编号就是 \(n-x+2\)。

然后我们思考带着旋转操作再维护新的节点编号：一个点被顺时针旋转了 \(k\) 其实就是将它的标号变大了 \(k\) 然后对 \(n\) 取模。

所以我们只需要记录当前的项链是否折叠 \(rev\) ，当前项链被旋转了多少颗珠子 \(push\) 然后来反解出当前询问的区间对应原项链上的区间就好了。

Code:

#include<bits/stdc++.h>
const int N=5e5+5;
using namespace std;
struct Tree{
    int lc,rc,tag,ans;
};
struct Segment_Tree{
    Tree t[N<<2];
    #define ls x<<1
    #define rs x<<1|1
    inline void paint(int x,int k)
    {
        t[x].lc=t[x].rc=t[x].tag=k;t[x].ans=1;
    }
    inline void pushdown(int x)
    {
        if(!t[x].tag)return;
        paint(ls,t[x].tag);paint(rs,t[x].tag);
    }
    inline Tree merge(Tree L,Tree R)
    {
        Tree T={L.lc ? L.lc : R.lc,R.rc ? R.rc : L.rc,0,0};
        T.ans=L.ans+R.ans-(L.rc==R.lc);
        return T;
    }
    void upd(int x,int l,int r,int L,int R,int k)
    {
        if(L<=l&&r<=R){paint(x,k);return;}
        int mid=l+r>>1;pushdown(x);
        if(L<=mid)upd(ls,l,mid,L,R,k);
        if(mid<R)upd(rs,mid+1,r,L,R,k);
        t[x]=merge(t[ls],t[rs]);
    }
    void query(int x,int l,int r,int L,int R,Tree &T)
    {
        if(L<=l&&r<=R){T=merge(T,t[x]);return;}
        int mid=l+r>>1;pushdown(x);
        if(L<=mid)query(ls,l,mid,L,R,T);
        if(mid<R)query(rs,mid+1,r,L,R,T);
    }
}T;
int push,rev;
int n,m,C;
char c[10];
int id(int x)
{
    if(rev)x=(push-x+2);
    else x=x-push;
    x=(x+n)%n;
    if(!x)x=n;
    return x;
}
void work()
{
    cin>>n>>C;
    for(int i=1,x;i<=n;i++)
    {
        scanf("%d",&x);T.upd(1,1,n,i,i,x);
    }
    cin>>m;
    for(int i=1,l,r,x;i<=m;i++)
    {
        scanf("%s",c);
        if(c[0]=='R')
        {
            scanf("%d",&x);
            push+=x;push%=n;
        }
        if(c[0]=='F')
        {
            rev^=1;push=(n-push+n)%n;
        }
        if(c[0]=='S')
        {
            scanf("%d%d",&l,&r);
            l=id(l),r=id(r);
            Tree L={0},R={0};
            T.query(1,1,n,l,l,L);T.query(1,1,n,r,r,R);
            T.upd(1,1,n,l,l,R.lc);T.upd(1,1,n,r,r,L.lc);
        }
        if(c[0]=='P')
        {
            scanf("%d%d%d",&l,&r,&x);
            l=id(l),r=id(r);if(rev)swap(l,r);
            if(l<=r){T.upd(1,1,n,l,r,x);}
            else{T.upd(1,1,n,l,n,x);T.upd(1,1,n,1,r,x);}
        }
        if(c[0]=='C'&&c[1]=='S')
        {
            scanf("%d%d",&l,&r);
            l=id(l),r=id(r);if(rev)swap(l,r);
            Tree ans={0};
            if(l<=r)T.query(1,1,n,l,r,ans);
            else
            {
                Tree res={0};
                T.query(1,1,n,l,n,ans);T.query(1,1,n,1,r,res);
                ans.ans=(ans.ans+res.ans-(ans.rc==res.lc));
            }
            printf("%d\n",ans.ans);
        }
        if(c[0]=='C'&&c[1]!='S')
        {
            Tree ans=T.t[1];
            ans.ans-=(ans.lc==ans.rc);
            ans.ans=max(ans.ans,1);
            printf("%d\n",ans.ans);
        }
        c[1]=' ';
    }
}
int main()
{
    //freopen("P4130_2.in","r",stdin);freopen("P4130.out","w",stdout);
    work();
    return 0;
}