P4219 [BJOI2014] 大融合

P4219 [BJOI2014] 大融合

题目描述

小强要在 \(N\) 个孤立的星球上建立起一套通信系统。这套通信系统就是连接 \(N\) 个点的一个树。

这个树的边是一条一条添加上去的。

在某个时刻，一条边的负载就是它所在的当前能够联通的树上路过它的简单路径的数量。

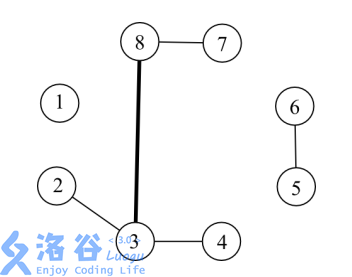
例如，在上图中，现在一共有了 \(5\) 条边。其中，\((3,8)\) 这条边的负载是 \(6\)，因为有六条简单路径 \(2-3-8\),\(2-3-8-7\),\(3-8,3-8-7\),\(4-3-8\),\(4-3-8-7\) 路过了 \((3,8)\)。

现在，你的任务就是随着边的添加，动态的回答小强对于某些边的负载的询问。

输入格式

第一行包含两个整数 \(N, Q\),表示星球的数量和操作的数量。星球从 \(1\) 开始编号。

接下来的 \(Q\) 行，每行是如下两种格式之一：

• A x y 表示在 \(x\) 和 \(y\) 之间连一条边。保证之前 \(x\) 和 \(y\) 是不联通的。
• Q x y表示询问 \((x,y)\) 这条边上的负载。保证 \(x\) 和 \(y\) 之间有一条边。

数据范围

对于所有数据，\(1≤N,Q≤10^5\)

说句闲话：

致敬传奇连控王 follow_mashiro 在给高一讲评本题时创造了40分钟让从零开始教 LCT 的壮举。然后结果就是高一昏昏欲睡，一心下播。

Solution:

言归正传，这题我们要维护一个略显奇怪的东西：该点在原树上的虚子树的大小。我们思考答案是如何统计的：对于一条边 (x,y) 它的负载应该为从x出发，不经过(x,y),能到达的点的个数 \(siz_x\) \(\times\) 从y出发，不经过(x,y),能到达的点的个数 \(siz_y\)

那么我们在 splite(x,y) 时就指定了包含 \(x,y\) 连通块 \(G(x,y)\) 对于 \(x\) 来说有且仅有一个实儿子 \(y\) ，也就是说，在 splite(x,y) 之后，根节点所在的平衡树上其实只有 \(x,y\) 两个节点，那么此时，x的虚子树大小正好就是我们所求的 \(siz_x-1\) ( \(x\) ,本身也算在 \(siz_x\) 里) ,\(y\) 同理。

那么我们如何维护虚子树大小呢？很简单，我们在access时，splay(x) 之后，由于x没有左儿子，x 的右儿子的大小其实就是 x的子树大小(不论虚实)，然后 y 的大小是 x 的实子树的大小，二者作差即可。

Code:

#include<bits/stdc++.h>
#define ll long long
const int N=2e5+5;
using namespace std;
int n,m;
struct LCT{
    struct Tree{
        int ch[2],ans,siz,tag,ff;
    }t[N];
    #define ls t[x].ch[0]
    #define rs t[x].ch[1]
    #define fa t[x].ff
    inline bool isnt_root(int x){return (t[fa].ch[0]==x||t[fa].ch[1]==x);}
    inline void pushup(int x)
    {
        t[x].siz=t[ls].siz+t[rs].siz+t[x].ans+1;
    }
    inline void rev(int x)
    {
        swap(t[x].ch[0],t[x].ch[1]);t[x].tag^=1;
    }
    void pushdown(int x)
    {
        if(!t[x].tag)return ;t[x].tag=0;
        if(ls)rev(ls);if(rs)rev(rs);
    }
    void rotate(int x)
    {
        int y=fa,z=t[fa].ff,k=(t[fa].ch[1]==x);

        if(isnt_root(y))t[z].ch[t[z].ch[1]==y]=x;
        t[x].ff=z;

        t[y].ch[k]=t[x].ch[!k];
        if(t[x].ch[!k])t[t[x].ch[!k]].ff=y;

        t[x].ch[!k]=y;
        t[y].ff=x;

        pushup(y);
    }
    int st[N]={0};
    void splay(int x)
    {
        int y=x,z=0;
        st[++st[0]]=y;
        while(isnt_root(y))st[++st[0]]=y=t[y].ff;
        while(st[0])pushdown(st[st[0]--]);
        while(isnt_root(x))
        {
            y=fa,z=t[fa].ff;
            if(isnt_root(y))rotate((t[z].ch[1]==y)==(t[y].ch[1]==x) ? y : x);
            rotate(x);
        }
        pushup(x);
    }
    void access(int x)
    {
        int y=0;
        while(x)
        {
            splay(x);
            t[x].ans+=t[rs].siz-t[y].siz;
            rs=y;pushup(x);y=x;x=fa;
        }
    }
    void make_root(int x)
    {
        access(x);splay(x);rev(x);
    }
    void splite(int x,int y)
    {
        make_root(x);access(y);splay(y);
    }
    void link(int x,int y)
    {
        splite(x,y);
        fa=y;
        t[y].ans+=t[x].siz;
        pushup(y);
    }
}T;
char c;
void work()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)T.t[i].siz=1;
    for(int i=1,x,y;i<=m;i++)
    {
        cin>>c;
        cin>>x>>y;
        if(c=='A')
        {
            T.link(x,y);
        }
        else
        {
            T.splite(x,y);
            ll ans=1ll*(T.t[x].ans+1)*(T.t[y].ans+1);
            printf("%lld\n",ans);
        }
    }
}
int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    work();
    return 0;
}