P3165 [CQOI2014] 排序机械臂

P3165 [CQOI2014] 排序机械臂

题目描述

为了把工厂中高低不等的物品按从低到高排好序，工程师发明了一种排序机械臂。它遵循一个简单的排序规则，第一次操作找到高度最低的物品的位置 \(P_1\) ，并把左起第一个物品至 \(P_1\) 间的物品 (即区间 \([1,P_1]\) 间的物品) 反序；第二次找到第二低的物品的位置 \(P_2\) ，并把左起第二个至 \(P_2\) 间的物品 (即区间 \([2,P_2]\) 间的物品) 反序……最终所有的物品都会被排好序。

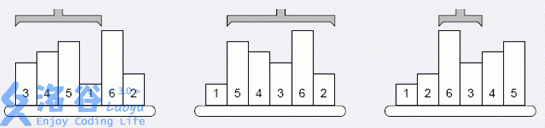
上图给出有六个物品的示例，第一次操作前，高度最低的物品在位置 \(4\) ，于是把第一至第四的物品反序；第二次操作前，第二低的物品在位罝六，于是把第二至六的物品反序……

你的任务便是编写一个程序，确定一个操作序列，即每次操作前第 \(i\) 低的物品所在位置 \(P_i\) ，以便机械臂工作。需要注意的是，如果有高度相同的物品，必须保证排序后它们的相对位置关系与初始时相同。

提示

\(N \le 100000\)

\(P_i \le 10^7\)

Solution:

拿到题目，区间翻转？这不纯文艺平衡树吗?

我们在以编号建一颗平衡树，平衡树节点上挂当前节点的权值以及区间翻转的 \(tag\) 然后我们唯一剩下的问题就是如何在一颗以下标建树的平衡树上查询区间最小值及其编号

我们在每个点上再挂一个值
\(t[x].mi=min{(t[x].val,t[ls],mi,t[rs].mi)}\)

然后查询的时候判断一下 \(t[x].mi\) 落在那个部分就好了

查询最小值：

int find(int x)
{
    int k=1;
    while(1)
    {
        pushdown(x);
        int ls=t[x].ls,rs=t[x].rs;
        if(t[x].mi==t[x].val){k+=t[ls].siz;return k;}
        else
        {
            if(ls&&t[ls].mi==t[x].mi){x=ls;}
            else if(rs&&t[rs].mi==t[x].mi){k+=t[ls].siz+1;x=rs;}
        }

    }
}

Code:

#include<bits/stdc++.h>
const int N=1e5+5;
const int inf=1e7;
using namespace std;
int n,m,cnt,rt;
// FHQ - Treap
struct Tree{
    int ls,rs,tag,val,siz,pri,mi;
}t[N];
int rd(){return rand()*rand()+rand()*17;}
int new_Node(int x)
{
    t[++cnt]=Tree{0,0,0,x,1,rd(),x};
    return cnt;
}
void pushup(int x)
{
    int ls=t[x].ls,rs=t[x].rs;
    t[x].siz=t[ls].siz+t[rs].siz+1;
    t[x].mi=t[x].val;
    if(ls)t[x].mi=min(t[x].mi,t[ls].mi);
    if(rs)t[x].mi=min(t[x].mi,t[rs].mi);
}
void pushdown(int x)
{
    if(!t[x].tag)return;
    swap(t[x].ls,t[x].rs);
    t[t[x].ls].tag^=1;
    t[t[x].rs].tag^=1;
    t[x].tag=0;
}
void splite(int x,int k,int &a,int &b)
{
    if(!x){a=b=0;return ;}
    pushdown(x);
    int tmp=t[t[x].ls].siz+1;
    if(k>=tmp){a=x;splite(t[x].rs,k-tmp,t[x].rs,b);}
    else {b=x;splite(t[x].ls,k,a,t[x].ls);}
    pushup(x);
}
int merge(int x,int y)
{
    if(!x||!y){return x+y;}
    if(t[x].pri<t[y].pri)
    {
        pushdown(x);
        t[x].rs=merge(t[x].rs,y);
        pushup(x);
        return x;
    }
    else
    {
        pushdown(y);
        t[y].ls=merge(x,t[y].ls);
        pushup(y);
        return y;
    }
}
int find(int x)
{
    int k=1;
    while(1)
    {
        pushdown(x);
        int ls=t[x].ls,rs=t[x].rs;
        if(t[x].mi==t[x].val){k+=t[ls].siz;return k;}
        else
        {
            if(ls&&t[ls].mi==t[x].mi){x=ls;}
            else if(rs&&t[rs].mi==t[x].mi){k+=t[ls].siz+1;x=rs;}
        }

    }
}
struct Node{
    int val,id;
    bool operator <(const Node &n)const{

        return val==n.val ? id<n.id : val<n.val;
    }
}q[N];
int a[N];
void work()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    scanf("%d",&q[i].val),q[i].id=i;
    sort(q+1,q+1+n);
    for(int i=1;i<=n;i++)a[q[i].id]=i;
    for(int i=1;i<=n;i++)rt=merge(rt,new_Node(a[i]));
    for(int i=1;i<=n;i++)
    {
        int k=find(rt),x,y,z;
        splite(rt,k-1,x,y);//x:[1,k-1] y:[k,n]
        splite(y,1,y,z);
        t[x].tag^=1;
        rt=merge(x,z);
        printf("%d ",k+i-1);
    }

}
int main()
{
    srand(7758258);
    //freopen("P3165.in","r",stdin);freopen("P3165.out","w",stdout);
    work();
    return 0;
}