P2542 [AHOI2005] 航线规划
P2542 [AHOI2005] 航线规划
题目描述
对 Samuel 星球的探险已经取得了非常巨大的成就,于是科学家们将目光投向了 Samuel 星球所在的星系——一个巨大的由千百万星球构成的 Samuel 星系。
星际空间站的 Samuel II 巨型计算机经过长期探测,已经锁定了 Samuel 星系中 \(n\) 个星球的空间坐标,并对这些星球以 \(1\) 至 \(n\) 依次编号。
一些先遣飞船已经出发,在星球之间开辟探险航线。
探险航线是双向的,例如从 \(1\) 号星球到 \(3\) 号星球开辟探险航线,那么从 \(3\) 号星球到 \(1\) 号星球也可以使用这条航线。
例如下图所示:
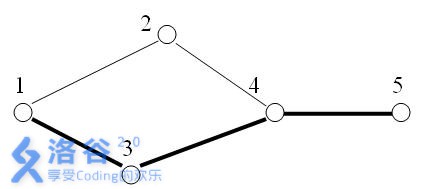
在 \(5\) 个星球之间,有 \(5\) 条探险航线。
\(A,B\) 两星球之间,如果某条航线不存在,就无法从 \(A\) 星球抵达 \(B\) 星球,我们则称这条航线为关键航线。
显然上图中,\(1\) 号与 \(5\) 号星球之间的关键航线有 \(1\) 条:即为 \(4\leftrightarrow5\) 航线。
然而,在宇宙中一些未知的磁暴和行星的冲撞,使得已有的某些航线被破坏,随着越来越多的航线被破坏,探险飞船又不能及时恢复这些航线,可见两个星球之间的关键航线会越来越多。
假设在上图中,航线 \(4\leftrightarrow2\)(从 \(4\) 号星球到 \(2\) 号星球)被破坏。此时,\(1\) 号与 \(5\) 号星球之间的关键航线就有 \(3\) 条:\(1 \leftrightarrow 3\),\(3 \leftrightarrow 4\),\(4 \leftrightarrow 5\)。
小联的任务是,不断关注航线被破坏的情况,并随时给出两个星球之间的关键航线数目。现在请你帮助完成。
输入格式
第一行有两个整数,分别表示星球个数 \(n\) 和初始时的航线条数 \(m\)。
接下来 \(m\) 行,每行有两个不相同的整数 \(u, v\),表示星球 \(u\) 和星球 \(v\) 之间存在一条航线。
接下来有若干行,每行首先给出一个整数 \(op\),表示一次操作的类型。
- 若 \(op = 1\),则后接两个整数 \(u, v\),表示询问当前 \(u, v\) 两星球之间有多少关键航线。
- 若 \(op = 0\),则后接两个整数 \(u, v\),表示 \(u, v\) 之间的航线被破坏。
- 若 \(op = -1\),则表示输入结束,后面不再存在操作。
输出格式
对每个 \(op = 1\) 的询问,输出一行一个整数表示关键航线数目。
提示
数据规模与约定
对于全部的测试点,保证:
- \(1 \leq n \leq 3 \times 10^4\),\(1 \leq m \leq 10^5\)。
- \(-1 \leq op \leq 1\),\(1 \leq u, v \leq n\)。
- 无论航线如何被破坏,任意时刻任意两个星球都能够相互到达。在整个数据中,任意两个星球之间最多只可能存在一条直接的航线。
- 对于 \(op = 0\) 的操作,保证操作前航线 \(u \leftrightarrow v\) 存在。
- 询问与破坏航线的总次数不超过 \(4 \times 10^4\)。
Solution:
首先我们注意到提示中的一句话:
无论航线如何被破坏,任意时刻任意两个星球都能够相互到达
这启示我们这这个图的连通性是始终不变的,于是我们可以将所有的问题离线并将时间反演,于是我们的问题就变成了如何在一颗树上加边并维护“关键航线数目”
那么有人可能要问了:那如果在op=-1时,原图还没有被删成树呢?当然是继续删啊笨蛋
显然,我们只需要一棵树,所以在遇到删完后不为树的情况,我们在dfs时钦定一些边为树边,然后将剩下的非树边在时间的末尾删除,显然这样不会对于答案造成影响也十分好写
至于如何钦定:显然对于一条有向边 u->v:当且仅当v在之前被访问过了(认父边除外),u->v为非树边
然后我们成功的将问题转化为了在一颗树上不断的加边,然后维护“关键航线数目”:
显然,对于一次加边\(u->v\),\(u->v\)显然是一条非树边。纯纯废话
它会使得 \(u->lca->v\)这段路上所有的边都变成"非关键航线".
这很难不让我们联想到树链剖分:
所以我们需要做的是:建一颗线段树维护每个节点的父边,初始值为1,然后对于每次连边u->v:将u->v上的所有边赋值为0,然后每次查询u->v路径上的总和
显然,树链剖分板子
我们数据结构选手就是看什么都是板子捏
然后要特别注意的是:
我们维护的是认父边,所以当树剖LCA进行到最后一次时,
假定dep[x]>dep[y]:
那么y就是lca,注意我们要维护的是u->lca和v->lca这两段,然而dfn[lca]对应的边是lca的认父边,所以我们在
update和query时应操作的区间是\([dfn_y+1,dfn_x]\)
然后这题就愉快的做完了
(又水了30分钟总结,开心捏)
Code:
#include<bits/stdc++.h>
const int N=4e5+5;
using namespace std;
vector<int> E[N],Q[N],ans;
int n,m,cnt,tot;
struct task{
int opt,x,y;
}q[N<<2],e[N<<2];
int now[N],top[N],dep[N],dfn[N],f[N],son[N],siz[N];
int rid[N];
void dfs1(int x,int fa)
{
dep[x]=dep[fa]+1;f[x]=fa;
siz[x]=1;
for(int i=0;i<E[x].size();i++)
{
int to=E[x][i];
if(to==fa)continue;
if(dep[to]){q[++cnt]=(task){0,x,to};E[x][i]=fa;continue;}
dep[to]=dep[x]+1;
dfs1(to,x);
son[x]= siz[to]>siz[son[x]] ? to : son[x];
siz[x]+=siz[to];
}
}
void dfs2(int u,int tp)
{
top[u]=tp;dfn[u]=++tot;rid[u]=tot;
if(!son[u])return ;
dfs2(son[u],tp);
for(int i=0,v;i<E[u].size();i++)
{
v=E[u][i];
if(v==f[u]||v==son[u])continue;
dfs2(v,v);
}
}
//Segmengt_Tree
#define ls x<<1
#define rs x<<1|1
struct Tree{
int val,l,r,tag;
}t[N<<2];
void pushup(int x)
{
t[x].val=t[ls].val+t[rs].val;
}
void pushdown(int x)
{
if(!t[x].tag){t[ls].tag=t[rs].tag=t[ls].val=t[rs].val=0;}
}
void build(int x,int l,int r)
{
t[x].l=l,t[x].r=r;
t[x].tag=1;
if(l==r)
{
t[x].val= l==1? 0:1;
return ;
}
int mid=l+r>>1;
build(ls,l,mid);
build(rs,mid+1,r);
pushup(x);
}
void upd(int x,int ll,int rr)
{
if(ll>rr)return;
if(ll<=t[x].l&&t[x].r<=rr)
{
t[x].val=0;
t[x].tag=0;
return ;
}
int mid=t[x].l+t[x].r>>1;
pushdown(x);
if(ll<=mid)upd(ls,ll,rr);
if(mid<rr)upd(rs,ll,rr);
pushup(x);
}
void query(int x,int ll,int rr,int &res)
{
if(ll<=t[x].l&&t[x].r<=rr)
{
res+=t[x].val;
return;
}
int mid=t[x].l+t[x].r>>1;
pushdown(x);
if(ll<=mid)query(ls,ll,rr,res);
if(mid<rr)query(rs,ll,rr,res);
}
int LCA(int x,int y)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])swap(x,y);
x=f[top[x]];
}
return dep[x]<dep[y] ? x : y;
}
void chain_upd(int x,int y)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])swap(x,y);
upd(1,dfn[top[x]],dfn[x]);
x=f[top[x]];
}
if(x==y)return ;
if(dep[x]<dep[y])swap(x,y);
upd(1,dfn[y]+1,dfn[x]);
return ;
}
int chain_query(int x,int y)
{
int res=0;
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])swap(x,y);
query(1,dfn[top[x]],dfn[x],res);
x=f[top[x]];
}
if(x==y)return res;
if(dep[x]<dep[y])swap(x,y);
query(1,dfn[y]+1,dfn[x],res);
return res;
}
#undef ls
#undef rs
//end
map<pair<int,int>,int> Map;
#define mp(x,y) make_pair(x,y)
int use[N];
int find(int x){f[x]= f[x]==x ? f[x]: find(f[x]);return f[x];}
void work()
{
cin>>n>>m;
for(int i=1,x,y;i<=m;i++)
{
scanf("%d%d",&x,&y);
e[i]=(task){-1,x,y};
}
for(int i=1;i<=n;i++){f[i]=i;}
for(int &i=++cnt;i;i++)
{
scanf("%d%d%d",&q[i].opt,&q[i].x,&q[i].y);
if(q[i].opt==-1)break;
if(q[i].opt==0)
{
Map[mp(q[i].x,q[i].y)]=Map[mp(q[i].y,q[i].x)]=1;
}
}
for(int i=1;i<=m;i++)
{
int u=find(e[i].x),v=find(e[i].y);
if(!Map[mp(e[i].x,e[i].y)])
{
if(u!=v)
{
f[v]=u;
use[i]=1;
E[e[i].x].push_back(e[i].y);
E[e[i].y].push_back(e[i].x);
}
else
{
q[++cnt]=(task){0,e[i].x,e[i].y};
}
}
}
for(int i=0;i<N;i++){f[i]=0;}
dfs1(1,0);
dfs2(1,1);
build(1,1,n);
for(int i=cnt,x,y;i;i--)
{
x=q[i].x,y=q[i].y;
if(q[i].opt==0)
{
chain_upd(x,y);
}
if(q[i].opt==1)
{
ans.push_back(chain_query(x,y));
}
}
for(int i=ans.size()-1;~i;i--){printf("%d\n",ans[i]);}
}
int main()
{
work();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号