计算思维期末复习

计算机导论重点知识点

1. 斐波那契数列（Fibonacci Sequence）

基本定义：
斐波那契数列是一种采用递推方式定义的数列，其特点是：从第三项开始，每一项等于前两项之和。

结构特点：

  • 初始条件：

    \[F(0)=0,\quad F(1)=1 \]

  • 递推关系式：

    \[F(n)=F(n-1)+F(n-2)\quad (n\ge 2) \]

  • 计算思想：
    该数列的定义过程体现了递归思想，同时也可以通过循环实现，体现了迭代思想。

作用与意义：

  • 是讲解递归程序设计的经典示例
  • 用于分析递归算法的时间复杂度问题，朴素递归实现具有指数级增长特征
  • 为动态规划思想提供引入案例，说明“重叠子问题”和“最优子结构”的概念

2. Bloom 分类法（教材对齐）

基本定义：
Bloom 教育目标分类法是一种从知识类型和认知过程水平两个维度来描述学习目标的分类体系，在计算机科学导论课程中用于刻画学生对计算机知识与计算思维的掌握程度。

（一）知识维度（What to know）

知识维度描述的是学习内容本身的类型，在计算机科学导论中主要包括：

  1. 事实性知识
    指计算机领域中的基本符号、术语和约定，如常数 (e)、大 O 表示法等。

  2. 概念性知识
    指对理论、原理和方法的理解，如程序中关键字的含义、大 O 表示法用于评估算法效率的方法，以及 RSA 公开密钥密码系统的基本原理。

  3. 程序性知识
    指完成某项任务的方法和过程，通常以算法形式出现，例如求解某一问题的算法，或构建 RSA 公开密钥密码系统的步骤。

  4. 元认知知识
    指对自身认知过程和问题复杂性的认识，在计算机导论中体现为计算思维相关内容，如分层抽象策略、启发式求解策略、对计算复杂性的理解（P 类问题、NP 类问题），以及对计算模型（概念模型和形式模型）的认识。

（二）认知过程维度（How to think）

认知过程维度描述的是学生对知识掌握的深度和水平，由低到高分为六个层次：

  1. 回忆
    能够记住与某个概念相关的信息，如程序、循环和迭代的定义。

  2. 理解
    能用自己的语言解释概念，例如说明程序与食谱在结构上的相似性，或解释循环迭代的含义。

  3. 应用
    能将概念应用到具体问题中，如跟踪一个包含循环结构的程序，并指出其输入与输出。

  4. 分析
    能将程序或问题分解成若干组成部分，例如分析一个循环程序的初始条件、循环条件和终止条件。

  5. 评估
    能对程序或方案的价值作出判断，如从效率或合理性角度评价一个循环程序。

  6. 创造
    能综合已有知识，设计新的程序或解决方案，例如设计一个包含循环结构的程序来解决特定问题。

在课程中的意义：
在计算机导论中，学生若仅达到回忆和理解层次，属于初级水平；达到应用和分析层次，属于中级水平；能够进行评估和创造，则体现出较高层次的计算思维能力。

3. 软件开发方法（Software Development Methods）

基本定义：
软件开发方法是对软件从需求到交付全过程进行组织和管理的过程模型。

主要阶段：

  • 需求分析
  • 系统设计
  • 编码实现
  • 测试
  • 维护

常见方法：

  • 瀑布模型
  • 原型模型
  • 增量模型
  • 敏捷开发方法

作用与意义：

  • 规范软件开发流程
  • 提高开发效率和软件质量
  • 降低项目风险

4. 阿克曼函数（Ackermann Function）

核心定位：
阿克曼函数是一个高度递归、增长极快的数学函数，常用于说明递归的复杂性极限。

一、基本定义（递归形式）

阿克曼函数通常定义为二元函数 \(A(m,n)\)，其递归关系为：

\[A(m,n)= \begin{cases} n+1, & m=0 \ A(m-1,1), & m>0,\ n=0 \ A(m-1, A(m,n-1)), & m>0,\ n>0 \end{cases} \]

特点说明：

  • 递归定义中递归调用自身；
  • 第三种情况出现了递归嵌套递归（非常关键）。

二、结构特点（结合定义理解）

从递推式本身即可看出阿克曼函数的“变态之处”：

  • 递归层次极深

    \[A(m,n) \rightarrow A(m-1, A(m,n-1)) \]

    一次调用中又产生新的递归调用。

  • 增长速度极快
    即使 \(m,n\) 很小，结果也会迅速变得非常大。

  • 非原始递归函数
    阿克曼函数的增长速度超过任何原始递归函数。

三、小规模计算示例（直观理解）

以 \(m=0,1,2\) 为例：

  1. 当 \(m=0\)：

    \[A(0,n)=n+1 \]

  2. 当 \(m=1\)：

    \[\begin{aligned} A(1,0)&=A(0,1)=2 \ A(1,n)&=n+2 \end{aligned} \]

  3. 当 \(m=2\)：

    \[\begin{aligned} A(2,0)&=A(1,1)=3 \ A(2,n)&=2n+3 \end{aligned} \]

  4. 当 \(m=3\)（增长开始失控）：

    \[A(3,n)=2^{n+3}-3 \]

四、作用与意义

  • 说明递归的复杂性
    阿克曼函数展示了递归调用可能带来的爆炸式计算复杂度。

  • 理论计算机科学中的极端例子
    常用于区分：

    • 原始递归函数
    • 一般递归函数

  • 并查集时间复杂度分析
    在并查集中，路径压缩后的时间复杂度为：

    \[O(\alpha(n)) \]

    其中 \(\alpha(n)\) 是反阿克曼函数，增长极其缓慢，在实际问题中近似为常数。

5. 哈密尔顿路径与回路（Hamiltonian Path / Cycle）

基本定义：

  • 哈密尔顿路径：图中经过每个顶点一次且仅一次的路径
  • 哈密尔顿回路：起点和终点相同的哈密尔顿路径

结构特点：

  • 关注的是顶点
  • 不允许顶点重复

作用与意义：

  • 图论中的经典问题
  • 旅行商问题的理论基础
  • 判定问题属于 NP 完全问题

6. 欧拉路径与欧拉回路（Euler Path / Cycle）

基本定义：

  • 欧拉路径：经过图中每条边一次且仅一次
  • 欧拉回路：起点终点相同的欧拉路径

结构特点：

  • 关注的是边
  • 顶点可以重复

判定条件：

  • 图是连通的
  • 奇度顶点数为 0 或 2

作用与意义：

  • 判断图的可遍历性
  • 解决实际路径规划问题

7. RSA 算法

基本定义：
RSA 是一种基于大整数因数分解困难性的公开密钥密码算法。

基本结构：

  • 公钥：用于加密
  • 私钥：用于解密
  • 基于两个大素数生成密钥

作用与意义：

  • 实现安全通信
  • 支持数字签名
  • 广泛应用于网络安全系统

8. ER 图（实体–联系图）

基本定义：
ER 图是一种用于数据库概念结构设计的图形化表示方法。

基本组成元素：

  • 实体：矩形表示
  • 属性：椭圆表示（主键加下划线）
  • 联系：菱形表示

联系类型：

  • 一对一（1:1）
  • 一对多（1:N）
  • 多对多（M:N）

作用与意义：

  • 抽象现实世界数据模型
  • 是关系数据库表设计的基础

9. Vocomputer

基本定义：
Vocomputer 是用于教学的抽象计算机模型。

作用与意义：

  • 帮助理解计算机基本组成
  • 演示程序执行过程
  • 理解冯·诺依曼体系结构

10. 数据结构（Data Structure）

基本定义：
数据结构是数据的组织形式及其操作方法。

主要分类：

  • 线性结构：数组、链表、栈、队列
  • 非线性结构：树、图、堆

作用与意义：

  • 决定程序的效率
  • 是算法设计的重要基础

11. 蒙特卡洛方法（Monte Carlo Method）

核心定位：
蒙特卡洛方法是一类基于随机抽样与概率统计思想的数值计算方法，通过大量随机实验来近似求解问题。

一、基本定义

蒙特卡洛方法通过在随机变量的取值空间中进行大量随机采样，利用样本统计量来近似目标问题的数值结果。

若随机变量为 \(X\)，其数学期望为：

\[E(X)=\int X f(X),dX \]

则可用 \(N\) 次随机采样的平均值进行近似：

\[E(X)\approx \frac{1}{N}\sum_{i=1}^{N}X_i \]

二、结构特点（结合数学形式）

  • 依赖随机抽样
    随机样本 \(X_1,X_2,\dots,X_N\) 服从给定概率分布。

  • 通过统计规律逼近真实值
    当 \(N\) 足够大时，根据大数定律：

    \[\frac{1}{N}\sum_{i=1}^{N}X_i \rightarrow E(X) \]

  • 精度随样本数量提高而提高
    误差通常与样本数满足：

    \[\text{误差} \sim \frac{1}{\sqrt{N}} \]

三、典型示例：利用蒙特卡洛方法估计 \(\pi\)

在边长为 \(2\) 的正方形内随机投点，其内接圆半径为 \(1\)。

  • 正方形面积：\(4\)
  • 圆面积：\(\pi\)

随机生成 \(N\) 个点，设其中落入圆内的点数为 \(M\)，则：

\[\frac{M}{N}\approx \frac{\pi}{4} \]

从而得到 \(\pi\) 的近似值：

\[\pi \approx 4\cdot \frac{M}{N} \]

四、作用与意义（考试高频表述）

  • 解决解析解难以获得的问题
    适用于高维积分、复杂模型计算。

  • 算法实现简单、通用性强
    不依赖问题的具体解析结构。

  • 广泛应用于多个领域
    包括：

    • 数值仿真与统计计算
    • 物理模拟与金融工程
    • 人工智能与强化学习

总结

蒙特卡洛方法是一种基于随机抽样和概率统计的数值计算方法，通过大量随机实验近似求解复杂问题，适用于解析解难以获得的情形。

12. 统计学方法（计算学科中的常用工具）

（1）全概率公式

基本思想：
将一个复杂事件拆分为若干互斥且完备的子事件，再计算其总概率。

数学形式：

设 \({B_1,B_2,\dots,B_n}\) 为样本空间的一个划分，则事件 \(A\) 的概率为：

\[P(A)=\sum_{i=1}^{n}P(B_i),P(A\mid B_i) \]

作用与意义：

  • 将复杂概率问题转化为多个简单条件概率问题
  • 是贝叶斯公式的理论基础

（2）贝叶斯公式

基本思想：
在已知结果的情况下，反向推断原因的概率。

数学形式：

\[P(B_i\mid A)=\frac{P(B_i)P(A\mid B_i)}{P(A)} \]

其中：

\[P(A)=\sum_{j=1}^{n}P(B_j),P(A\mid B_j) \]

作用与意义：

  • 将先验概率更新为后验概率
  • 用于不确定性推理与概率推断

（3）朴素贝叶斯方法

基本思想：
在贝叶斯公式基础上，假设各特征在给定类别条件下相互独立。

数学形式：

设特征向量为 \(X=(x_1,x_2,\dots,x_n)\)，类别为 \(C_k\)：

\[P(C_k\mid X)\propto P(C_k)\prod_{i=1}^{n}P(x_i\mid C_k) \]

作用与意义：

  • 计算简单、效率高

  • 广泛应用于：

    • 文本分类
    • 垃圾邮件识别

（4）梯度下降法

基本思想：
沿着函数梯度的反方向迭代更新参数，使目标函数逐步减小。

数学形式：

设目标函数为 \(f(\theta)\)，学习率为 \(\eta\)，则更新公式为：

\[\theta_{k+1}=\theta_k-\eta\nabla f(\theta_k) \]

作用与意义：

  • 用于求函数最小值
  • 是机器学习模型参数优化的核心方法

（5）最小二乘法

基本思想：
通过最小化预测值与实际值之间误差平方和来确定模型参数。

数学形式：

设样本点为 \((x_i,y_i)\)，模型预测值为 \(\hat y_i\)：

\[\min \sum_{i=1}^{n}(y_i-\hat y_i)^2 \]

作用与意义：

  • 实现数据拟合
  • 是回归分析的基础方法

总结对比（一句话速记）

全概率与贝叶斯用于概率推断，朴素贝叶斯用于分类；
梯度下降用于优化，最小二乘用于拟合。

第一次平时测试

一、题目提取

题目1：图形的欧拉/哈密顿路径/回路判断

题干：判断下列图形是否存在欧拉路径、欧拉回路、哈密顿路径、哈密顿回路？如果存在，请写出路线。（共2小题，每小题8分）

img

img

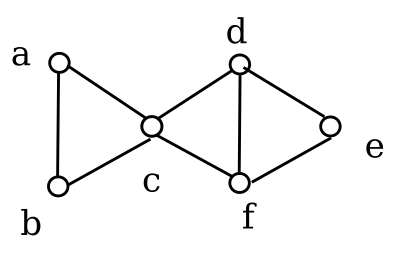
  • 第一个图形（顶点：a、b、c、d、f、e）
  1. 欧拉路径：存在
    • 依据：图连通，奇度顶点数为2（f：3度、e：1度）
    • 路径示例：( e \rightarrow f \rightarrow c \rightarrow b \rightarrow a \rightarrow c \rightarrow d \rightarrow f )（遍历所有7条边）
  2. 欧拉回路：不存在
    • 依据：奇度顶点数不为0（需所有顶点为偶度）
  3. 哈密顿路径：存在
    • 依据：存在经过所有顶点一次的路径
    • 路径示例：( a \rightarrow b \rightarrow c \rightarrow d \rightarrow f \rightarrow e )
  4. 哈密顿回路：不存在
    • 依据：顶点e仅与f相连，无法经过所有顶点后返回起点
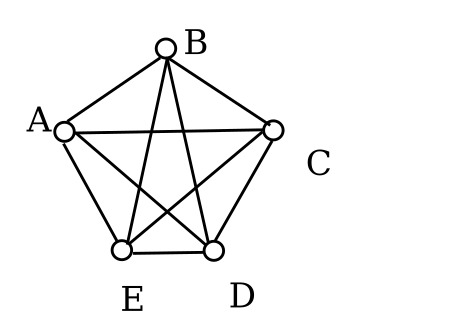
  • 第二个图形（五角星，顶点：A、B、C、D、E）
  1. 欧拉回路：存在
    • 依据：图连通，所有顶点度数均为2（偶度）
    • 回路示例：( A \rightarrow C \rightarrow E \rightarrow B \rightarrow D \rightarrow A )（遍历所有5条边）
  2. 欧拉路径：存在（欧拉回路是特殊的欧拉路径）
  3. 哈密顿回路：存在
    • 依据：五角星是哈密顿图，可经过所有顶点一次并返回起点
    • 回路示例：( A \rightarrow B \rightarrow C \rightarrow D \rightarrow E \rightarrow A )
  4. 哈密顿路径：存在（哈密顿回路是特殊的哈密顿路径）

题目2：RSA公钥系统构建与明文加密

题干：设$( p=11 \()，\)( q=17 \()，\)( n=11×17=187 $)，请构建一个RSA公钥密码系统，并对明文8加密。（要求写出构建公钥和私钥的过程、对明文加密的过程）（共15分）

题目2：RSA公钥系统构建与明文加密

题干：设$$ p=11 $$，$$q=17$$，$$n=11×17=187$$，请构建一个RSA公钥密码系统，并对明文8加密。（要求写出构建公钥和私钥的过程、对明文加密的过程）（共15分）

\[p=11$$，$$q=17 \]

\[n = pq = 11\times17 = 187 \]

\[\varphi(n)=(p-1)(q-1)=(11-1)\times(17-1)=10\times16=160 \]

\[\because 160 \bmod 3 = 1$$，且$$\gcd(3,160)=1$$（满足$$1<e<\varphi(n)$$且与$$\varphi(n)$$互质的条件） $$\therefore 令e=3\]

需满足$$ed \equiv 1 \pmod{\varphi(n)}$$，即存在整数$$k$$，使得：

\[3d - 160k = 1 \]

① $$3d - 160k = 1$$
② 简化求解思路，逐步推导系数为1的形式，直接令$$d = 1$$ 开始回代

回代：
将$$d=1$$代入简化关系：$$3\times1 - k = 1 \Rightarrow k=2$$
将$$k=2$$代入①式：$$3d - 160\times2 = 1$$

\[3d = 321 \Rightarrow d=107 \]

  • 补充：RSA密钥确定与明文加密过程

  1. 确定密钥

    • 公钥：$$(e,n)=(3,187)$$
    • 私钥：$$(d,n)=(107,187)$$

  2. 对明文$$M=8$$加密
    RSA加密公式为：

    \[C = M^e \pmod{n} \]

    代入数值计算：

    \[C = 8^3 \pmod{187} = 512 \pmod{187} \]

    计算$$512 \div 187$$，得商2余$$512-187\times2=512-374=138$$
    因此加密后的密文$$C=138$$

题目3：RSA密文解密

题干：在一个RSA公钥密码系统中，设私钥为( (3, 143) )，请对密文17解密。（共10分）

题目4：程序自终止判断

题干：判断以下3个程序是否属于自终止程序：（共3小题，每小题3分）
A.

while X not 0 do; 
end;

B.

while X not 0 do 
    X=X;
        end;

C.

X=X-1; 
while X not 0 do; 
end;

题目5：背包问题（贪婪算法）

题干：背包容量( W=150 )，7个物品（不可分割）的重量、价值如下表。用3种贪婪准则（价值优先、重量优先、单位重量价值优先）求解，比较哪种准则最优。（共10分）

物品 A B C D E F G
重量 35 30 60 50 40 10 25
价值 40 40 30 50 40 10 25

按物品价值从大到小选取：

\[D(50) > A(40)=B(40)=E(40) > G(25) > C(30) > F(10) \]

依次装入背包，设剩余容量为 (W)，总价值为 (V)：

\[W=150 \]

\[\text{选 }D(50,50)，W=150-50=100，V=50 \]

\[\text{选 }A(35,40)，W=100-35=65，V=90 \]

\[\text{选 }B(30,40)，W=65-30=35，V=130 \]

\[\text{选 }G(25,25)，W=35-25=10，V=155 \]

\[\text{选 }F(10,10)，W=10-10=0，V=165 \]

因此，价值优先策略得到：

\[V=165 \]

（二）重量优先贪婪策略

按物品重量从小到大选取：

\[F(10) < G(25) < B(30) < A(35) < E(40) < D(50) < C(60) \]

依次装入背包：

\[\text{选 }F(10,10)，W=150-10=140，V=10 \]

\[\text{选 }G(25,25)，W=140-25=115，V=35 \]

\[\text{选 }B(30,40)，W=115-30=85，V=75 \]

\[\text{选 }A(35,40)，W=85-35=50，V=115 \]

\[\text{选 }E(40,40)，W=50-40=10，V=155 \]

剩余容量不足以装入其他物品。

因此，重量优先策略得到：

\[V=155 \]

（三）单位重量价值优先贪婪策略

各物品单位重量价值为：

\[\frac{v}{w}_A=\frac{40}{35}\approx1.14,\quad \frac{v}{w}_B=\frac{40}{30}\approx1.33,\quad \frac{v}{w}_C=\frac{30}{60}=0.5 \]

\[\frac{v}{w}_D=\frac{50}{50}=1,\quad \frac{v}{w}_E=\frac{40}{40}=1,\quad \frac{v}{w}_F=\frac{10}{10}=1,\quad \frac{v}{w}_G=\frac{25}{25}=1 \]

按单位重量价值从大到小选取：

\[B > A > D=E=F=G > C \]

依次装入背包：

\[\text{选 }B(30,40)，W=150-30=120，V=40 \]

\[\text{选 }A(35,40)，W=120-35=85，V=80 \]

\[\text{选 }D(50,50)，W=85-50=35，V=130 \]

\[\text{选 }G(25,25)，W=35-25=10，V=155 \]

\[\text{选 }F(10,10)，W=10-10=0，V=165 \]

因此，单位重量价值优先策略得到：

\[V=165 \]

（四）比较与结论

\[\begin{aligned} &\text{价值优先： }V=165 \ &\text{重量优先： }V=155 \ &\text{单位重量价值优先： }V=165 \end{aligned} \]

题目6：图灵机“思维”的定义角度

题干：图灵是从什么角度判定机器是否能思维的？（或从什么主义定义“机器思维”？）（共6分）

图灵是从行为主义的角度判定机器是否能思维的。他不关注机器内部是否具有意识或真实的思维过程，而是通过图灵测试，根据机器在与人类对话中的外在行为表现是否与人类不可区分，来判断机器是否具有思维能力。

题目7：补全海伦算法的Raptor程序

题干：补全求平方根的“海伦算法”Raptor程序（精度0.0001）。（共6分）

Start（海伦算法求a的平方根的程序）
  ↓
提示"Enter a number"GET a → 获取a
  ↓
提示"Enter a number" → GET b（备注：猜测b初始值为6）
  ↓
Loop（循环）
  ↓
   判断：? # 答案是: abs(a - b*b ) < 0.0001
   → Yes: 输出b
         ↓
         End
   → No: b ← (b + a/b)/2
         ↓
         回到Loop

题目8：补全汉诺塔的Raptor子程序

题干：补全汉诺塔递归算法的move()子程序Raptor代码。（共6分）
这是汉诺塔问题的递归子程序（move），功能是借助y柱，将u个盘子从x柱移到z柱，极简文本流程：

Start（in u(入参:u个盘子), in x(入参:x柱子), in y(入参:y柱子),in z(入参:z柱子) (利用y柱作为辅助,将u个盘子从x移到z)
↓
判断：u = 1?
→ Yes: 输出x + " -> " + z
     ↓
     End
→ No:
     ↓
     调用move(u-1, x, z, y)（借助z柱，把u-1个盘子从x移到y）
     ↓
     输出x + " -> " + z
     ↓
     ? # 答案是: move(u-1, y, x, z)
     ↓
     End

目标：

利用 y 作为辅助，把 u 个盘子从 x 移到 z

当 u > 1 时，标准三步走：

把 u−1 个盘子
从 x → y（借助 z）

把最大的盘子
从 x → z

把刚才那 u−1 个盘子
从 y → z（借助 x）

你已经写了 1 和 2，
所以问号处必然是 第 3 步。
调用 move(u-1, y, x, z)

含义是：
左 → 中，左 → 右，中 → 右

对应到参数就是：

(u-1, x, z, y)
(x → z)
(u-1, y, x, z)借助 x 柱，把 u−1 个盘子从 y 移到 z

题目9：补全Raptor乘法程序

题干：补全求( a×b )的Raptor乘法程序。（共6分）
那我简化成纯文本+箭头的极简流程，去掉多余装饰：

  • main
Start
  ↓
提示"Input an integer" → 获取n
  ↓
调用mult(n, result)
  ↓
输出"n! equals to " + result
  ↓
End
  • mult
Start (in a, out b)
  ↓
判断a ≤ 1？
  → Yes: b ← 1
  → No:
      递归调用mult(?, b)  #答案是：mult(a - 1, b)
      ↓
      c ← b
      ↓
      b ← a * c
  ↓
End

题目10：选择/填空题

  1. （单选）阿姆达定律：( f=0.01% )，( p→∞ )，最大加速能力( s_p )为（）。（2分）

    a.10000 b.1000 c.100 d.10

阿姆达定律：

\[S_p=\frac{1}{f+\frac{1-f}{p}} \]

当 $(p \to \infty) $时：

\[S_{\max}=\frac{1}{f} \]

已知：

\[f=0.01%=0.0001 \]

\[S_{\max}=\frac{1}{0.0001}=10000 \]

正确答案：a. 10000

  1. 下列有关计算学科的定义及其根本问题，说法不正确的是（ ）。（共2分）

    A 计算学科是对描述和变换信息的算法过程进行的系统研究，包括理论、分析、设计、效率、实现和应用等。

    B 计算学科的根本问题是什么能被（有效地）自动进行。

    C 学科的根本问题隐藏于学科基本问题之中，或者说，是学科所有问题之中最基本的问题。

    D 计算学科不包括对计算过程的分析以及计算机的设计和使用。

  • A：这是 Denning 给出的标准定义，✔ 正确
  • B：这是计算学科的根本问题原话，✔ 正确
  • C：对“根本问题”的概括性表述，✔ 正确
  • D：说“不包括 对计算过程的分析以及计算机的设计和使用”，
    选 D

  1. 下列有关计算学科二维定义矩阵的说法不正确的是(D)。（共2分）

    该计算学科二维定义矩阵如下：

    学科知识领域 抽象 理论 设计
    1. 人工智能(artificial intelligence，AI)
    2. 算法与复杂性（algorithmic and complexity，AL）
    3. 体系结构与组织（architecture and organization，AR）
    4. 数据管理(data management，DM)
    5. 程序设计语言基础(foundations of programming languages，FPL)
    6. 图形学与交互技术(graphics and interactive techniques，GIT)
    7. 人机交互(human computer interaction，HCI)
    8. 数学与统计学基础（mathematical and statistical foundations，MSF）
    9. 网络与通信（networking and communication，NC）
    10. 操作系统（operating systems，OS）
    11. 并行与分布式计算（parallel and distributed computing，PD）
    12. 软件开发基础(software development fundamentals，SDF)
    13. 软件工程（software engineering，SE）
    14. 安全（security，SEC）
    15. 社会、伦理与职业化(society，ethics and professionalism，SEP)
    16. 系统基础（systems fundamentals，SF）
    17. 专业平台开发（specialized platform development，SPD）

    A 计算学科二维定义矩阵的概念为我们认知学科提供了一个模型。

    B 计算学科二维定义矩阵是对计算学科一个高度概括。

    C 计算学科二维定义矩阵横向一维由抽象、理论、设计等3个过程组成，根据CS2013报告，其纵向一维可划分为18个知识领域。

    D 在计算学科二维定义矩阵中，3个过程（学科形态）及其具体内容（值）都是不变的。

正确答案：D

A 选项解析：
计算学科二维定义矩阵通过“知识领域 × 学科形态”的方式，为理解计算学科整体结构提供了一个认知模型，表述正确。

B 选项解析：
计算学科二维定义矩阵对计算学科的主要研究内容和研究方式进行了高度抽象和概括，属于对学科整体的总结，表述正确。

C 选项解析：
计算学科二维定义矩阵横向由抽象、理论、设计三个过程组成；纵向依据 CS2013 报告可划分为 18 个知识领域，该说法符合教材与报告内容，表述正确。

D 选项解析：
计算学科二维定义矩阵中的抽象、理论、设计作为学科形态是相对稳定的，但其在不同知识领域中的具体内容会随着学科和技术的发展不断变化，因此“具体内容不变”的说法错误。

  1. 下列有关计算思维特征的说法不正确的是（ ）。（共2分）
    A 计算思维是概念化，不是程序化
    B 计算思维是根本的，不是刻板的技能
    C 计算思维是计算机的，不是人的思维
    D 计算思维是数学和工程思维的互补与融合

正确答案：C

A 选项解析：
计算思维强调问题的抽象、分解与建模，是一种概念层面的思维方式，而不是具体编程实现，表述正确。

B 选项解析：
计算思维是一种根本性的思维能力，适用于多领域问题解决，而非机械、刻板的操作技能，表述正确。

C 选项解析：
计算思维是人的思维方式，并非计算机自身具备的思维能力，将其说成“计算机的思维”是对计算思维内涵的误解，表述不正确。

D 选项解析：
计算思维与数学思维、工程思维相互补充、相互融合，共同支持复杂问题的分析与解决，表述正确。

  1. 验证一个问题的解是否正确远比找到一个问题的解要容易的多，这就是所谓的“证比求易”（Algorithm of verifying is easier than finding solutions）。
    比如，对于求48 770 428 433 377 171的一个真因子的问题，最坏情况下需要计算的次数大约为____；而验证223 092 827是否是真因子只需要1次。这个结论有重要的认知价值，与“评论别人的文章比写文章容易”类似，属于教育学中的元认知。（ ）（共2分）

    A 2亿
    B 2百亿
    C 2千亿
    D 2万亿

正确答案：A

A 选项解析：
对一个整数进行因子搜索，最坏情况下需要从 2 试除到其平方根为止。
对于 48 770 428 433 377 171，其平方根约为 (2.2 \times 10^8)，即约 2 亿次，表述正确。

B 选项解析：
2 百亿（(2 \times 10^{10})）远大于该数平方根量级，明显高估，错误。

C 选项解析：
2 千亿（(2 \times 10^{11})）与实际最坏情况计算次数不符，错误。

D 选项解析：
2 万亿（(2 \times 10^{12})）严重偏离实际计算规模，错误。

6 . “计算机科学导论”课程如何构建是计算教育面临的一个重大问题。对于如何解决该问题，下列阐述正确的是（ ）。（共3分）

A 《计算作为一门学科》报告确认了“计算机科学导论”课程的构建问题是一个重要问题。报告认为，该课程要培养学生面向学科的思维能力，使学生领会学科的力量以及从事本学科工作的价值之所在。报告希望该课程能用类似于数学那样严密的方式将学生引入计算学科各个富有挑战性的领域之中。

B CC2001报告认为，“计算机科学导论”课应该讲授学科中那些富有智慧的核心思想。

C CC2004和CC2005则进一步指出，该课程的关键是课程的结构设计问题。

D CS2001 Interim Review（草案）中将“计算思维”与“计算机科学导论”课程绑定在一起，明确要求“计算机科学导论”课程讲授计算思维的本质。

第6题 答案：ABCD

A 正确：《计算作为一门学科》报告明确强调导论课应培养面向学科的思维能力。
B 正确：CC2001 指出导论课应讲授计算学科中富有智慧的核心思想。
C 正确：CC2004/2005 进一步强调课程结构设计是关键。
D 正确：CS2001 Interim Review 将计算思维与“计算机科学导论”课程明确绑定。

7.（填空）下面程序能否自终止？（填能或否）。（共3分）

y=x;
while x not 0 do
    x=x-1;
end;
y=y-1;
while y not 0 do
    y=y-1;
end;

答案：否

解析：
程序是否自终止要求对任意输入都能在有限步内结束。
当 (x > 0) 时，第一个循环通过不断减 1 可终止；第二个循环同理。
但当 (x < 0) 时，while x not 0 do x = x - 1 会使 (x) 越来越小，永远不可能等于 0，程序无法终止，因此该程序不是自终止程序。

第二次平时测试

一、判断题

  1. 语言A的初始符号集为{a，b，c，d，e，(，)，+，−，×，÷}；形成规则为上述符号组成的有限符号串中凡以符号“(”开头的符号串为一公式。则A是一形式语言。（）
  1. 图灵机不仅可以计算S(x)=x+1（后继函数），显然还可以计算N(x)=0（零函数），甚至( U^{(n)}(x_1，x_2，…，x_n)=x_i )，( 1≤i≤n )（投影函数）以及这3个函数的任意组合。（）
  1. 冯·诺依曼型计算机等实现技术属于学科中理论形态的内容。（）
  1. 从原来对程序和数据的严格区别到一样看待，这个观念上的转变是计算机史上的一场革命。（）
  1. 虚拟机的层次之分有助于各层次计算机语言相对独立地发展，从而降低了计算机语言研制的复杂程度，使研制者可以将注意力主要放在本层次的语言上。（）
  1. 语言“创造性”过程的本质与计算过程的本质是完全不同的两码事。（）

二、选择题

（共8小题，每小题2分，共16分）

  1. 抽象（Abstraction）与自动化（Automation）是计算思维的本质特征，在计算学科各领域中均存在为数不少的抽象工具。E-R图（实体-联系图）就是其中一种对客观世界进行抽象的工具，使用该工具可以大大降低软件系统研制，特别是数据库应用系统研制的复杂性。
    一个公司有一个销售部门，一个销售部门有若干员工，每位员工都可以销售若干商品，每个商品都可以由若干员工销售，一个商品可以存放在若干不同的仓库中，一个仓库可以存放不同的商品，一个员工可以管理若干仓库，该单位销售部的E-R图（提示：销售时有一个“销售明细”属性；存放时有一个“存放与出库时间”的属性）如下所示，图中空白填写顺序应为（）。（共2分）
    img
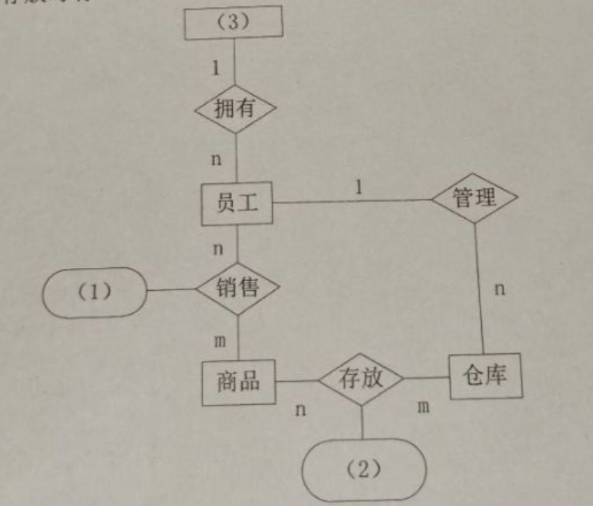
    选项：
    A. 销售明细 销售部门 存放与出库时间
    B. 存放与出库时间 销售明细 销售部门
    C. 销售明细 存放与出库时间 销售部门
    D. 销售部门 销售明细 存放与出库时间

2.（单选）计算机对语言进行处理，首先要解决的是语言的歧义性问题，给出句子“I saw the man on the hill with the telescope”，不可能解释为（ ）。（共2分）
A. I with the telescope
B. the man with the telescope
C. the hill with the telescope
D. I on the hill

  1. 如果一个关系有12条指令，请问操作码至少需要____位；若操作码有5位，那么最多可以设计____条指令。（共2分）
    A. 5，16
    B. 6，22
    C. 6，32
    D. 4，22
  1. 一般情况下，在关系树中，若“学生选课”关系，E-R图“学生选课”关系模型，“学生选课”关系模型，以下所听（ ）。（共2分）
    A. 能
    B. 理论
    C. 设计
    D. 不能

  1. （单选）Vcomputer机器有16个8位的通用寄存器，每个寄存器能容纳的数值范围为00~FF（十六进制数）。若存放超出此范围的数值，就会出现寄存器值的“溢出”。此时，Vcomputer机器自动截取该数值的低8位，存入寄存器。现有十六进制数10和FF，若将这两个数相加的结果存入寄存器0，则寄存器0中的数值为（ ）。（共2分）

    A. 10F
    B. 0F
    C. 87
    D. 8F

  1. （单选）Vcomputer机器指令由4位十六进制数构成（1位操作码，3位操作数），其机器指令集如下表所示。那么下列选项中的指令能表示“将地址为E8的内存单元的值装入寄存器R0中”的是（ ）。（共2分）
操作码 操作数 描 述
1 RXY 将主存XY单元中的数取出，存入寄存器R中。如1543，将主存43单元中的数取出，存入寄存器5中
2 RXY 将数XY存入寄存器R中。如2543，将43（十六进制数）存入寄存器5中
3 RXY 将寄存器R中的数取出，存入内存地址为XY的单元中
4 0RS 将寄存器R中的数存入寄存器S中
5 RST 将寄存器S与寄存器T中用补码表示的数相加，结果存入寄存器R中
6 R0X 将寄存器R中的数左移X位（先将R中的十六进制数转换为二进制数，再左移X位），移位后，用0填充腾空的位
7 R00 将寄存器R中的数按位取反。如7100，将寄存器1中的数按位取反，将结果存入寄存器1中
8 RXY 若寄存器R与寄存器0中的值相同，则将数据XY（转移地址）存入程序计数器；否则，程序按原来的顺序继续执行
9 000 停机，9000

A. 10E8
B. 1E80
C. 20E8
D. 2E80

  1. （单选）下表是Vcomputer机器的汇编指令与机器指令对照表，则下列用Vcomputer汇编指令实现“将数据01存入寄存器0中”正确的是（ ）。（共2分）
操作码 操作数 汇编指令 描 述
1 RXY Load R,[XY] [R]:=[XY]
2 RXY Load R,XY [R]:=XY
3 RXY Store R,[XY] [XY]:=[R]
4 0RS Mov R,S [S]:=[R]
5 RST Add R,S,T [R]:=[S]+[T]
6 R0X Shl R,X [R]:=[R]左移X位，移位后，用0填充腾空的位
7 R00 Not R [R]:=[R]中的值按位取反
8 RXY Jmp R, XY 程序计数器[PC]:=XY, IF [R]=[R0]; else[PC]:=[PC]+2
9 000 Halt 停机

A. Load R0,[01]
B. Load R0,01
C. Store R0,[01]
D. Mov R0,01

  1. （单选）Vcomputer机器指令由4位十六进制数构成（1位操作码，3位操作数），其机器指令集如下表所示，其中，操作码为8的机器指令是条件跳转指令。若当前寄存器0中的值为B0，寄存器1中的值为A0，寄存器2中的值为10，在执行指令8120，5112和8130后，则程序执行的下一条指令的地址为（ ）。（共2分）
操作码 操作数 描 述
1 RXY 将主存XY单元中的数取出，存入寄存器R中。如1543，将主存43单元中的数取出，存入寄存器5中
2 RXY 将数XY存入寄存器R中。如2543，将43（十六进制数）存入寄存器5中
3 RXY 将寄存器R中的数取出，存入内存地址为XY的单元中
4 0RS 将寄存器R中的数存入寄存器S中
5 RST 将寄存器S与寄存器T中用补码表示的数相加，结果存入寄存器R中
6 R0X 将寄存器R中的数左移X位（先将R中的十六进制数转换为二进制数，再左移X位），移位后，用0填充腾空的位
7 R00 将寄存器R中的数按位取反。如7100，将寄存器1中的数按位取反，将结果存入寄存器1中
8 RXY 若寄存器R与寄存器0中的值相同，则将数据XY（转移地址）存入程序计数器；否则，程序按原来的顺序继续执行
9 000 停机，9000

A) 20
B) 30
C) A0
D) 不确定

三

若一个特定的指令系统有12条指令，请问操作码至少应该设置为几位？若操作码只有1位，那么最多可以设计多少条指令？（共10分）

答案：
操作码至少需要 4 位；
若操作码只有 1 位，最多可设计 2 条指令。

解析：
操作码能够表示的指令条数为

\[2^k \]

其中，\(k\) 为操作码的位数。

要表示 \(12\) 条不同的指令，需要满足

\[2^k \ge 12 \]

由于

\[2^3 = 8 < 12,\quad 2^4 = 16 \ge 12 \]

因此，操作码至少需要 4 位。

当操作码只有 \(1\) 位时，可表示的指令数为

\[2^1 = 2 \]

四

画“学生信息E-R图”，要求在教材P55页 图3.1“学生选课E-R图”的基础上，增加学院（学院编号，学院名，学院负责人），以及学生班级（班级编号，班级名称，班长，所在学院）两个实体。新增两个实体后，实体间的联系为：一个学院有若干班级，一个班级有若干学生，一个学生可以选修若干门课程，一门课程可被若干学生选修。（共10分）

五

现有Brooks hear给出的有12条指令，操作码、操作数的含义如下表所示。（共4小题，每小题5分，共20分）

操作码 操作数 描 述
1 RXY 将内存XY单元中的数据取出，存入寄存器R中，如1A43：将43单元中的数据取出，存入寄存器A中
2 RXY 将数XY存放到寄存器R中
3 RXY 将寄存器R中的数据存入主存地址为XY的单元中
4 0RS 将寄存器R中的数存入寄存器S中
5 RST 将寄存器S与T中的用二进制补码表示的数相加，将结果存入寄存器R中
6 RST 将寄存器S与T中的用浮点数表示的数相加，将结果存入寄存器R中
7 RST 将寄存器S与T中的数进行或运算，将结果存入寄存器R中
8 RST 将寄存器S与T中的数进行与运算，将结果存入寄存器R中
9 RST 将寄存器S与T中的数进行异或运算，将结果存入寄存器R中
A ROX 将寄存器R中的数右移X次，每次将最低位移出的数字放在最高位的空缺中
B RXY 若寄存器R中的数与寄存器0中的数相同，则将数XY（转移指令）存入程序计数器中；否则，按原来的顺序继续执行
C 000 停机，C000

地址A6到B1的内存单元中包含以下内容：

地址 内容
A6 20
A7 A8
A8 11
A9 A8
AA 22
AB 20
AC 53
AD 01
AE 85
AF 23
B0 C0
B1 00

机器从A6开始执行，回答以下问题：
a. 若机器每微秒执行一条指令，那么完成这个程序要多少时间？
b. 将以上指令翻译成自然语言。
c. 程序结束时，寄存器5的值是多少？
d. 20A8与11A8的A8是一个意思吗？

内存地址按两位十六进制数编址（1个地址单元=1字节），每条指令为「1位十六进制操作码 + 3位十六进制操作数」（共4位十六进制，占2个连续内存地址单元）。
需将A6~B1的内存单元两两拼接为完整指令，拆分结果如下：

指令序号 占用内存地址 内存内容拼接 操作码+操作数
1 A6-A7 20 + A8 = 20A8 操作码2，操作数0A8
2 A8-A9 11 + A8 = 11A8 操作码1，操作数1A8
3 AA-AB 22 + 20 = 2220 操作码2，操作数220
4 AC-AD 53 + 01 = 5301 操作码5，操作数301
5 AE-AF 85 + 23 = 8523 操作码8，操作数523
6 B0-B1 C0 + 00 = C000 操作码C，操作数000

注：拼接后按「操作码（第1位）+ 操作数（后3位）」拆分，如20A8拆分为操作码2、操作数0A8；11A8拆分为操作码1、操作数1A8。

  • a. 程序执行时间
    机器从A6开始执行，共执行6条指令（含停机指令），且每微秒执行1条指令。
    执行时间 = 指令条数 × 单条指令执行时间 = \(6 × 1 = \boldsymbol{6}\) 微秒。
  • b. 指令翻译成自然语言
指令序号 操作码+操作数 自然语言翻译
1 2 0A8 操作码2：将立即数A8（十六进制）存放到寄存器0中。
2 1 1A8 操作码1：将内存A8单元中的数据取出，存入寄存器1中。
3 2 220 操作码2：将立即数20（十六进制）存放到寄存器2中。
4 5 301 操作码5：将寄存器0与寄存器1中的二进制补码数相加，结果存入寄存器3中。
5 8 523 操作码8：将寄存器2与寄存器3中的数进行与运算，结果存入寄存器5中。
6 C 000 操作码C：程序停机。

  • c. 程序结束时寄存器5的值

  • 步骤推导（初始状态：所有寄存器=0，未提及的内存单元=0）

  1. 指令1执行：R0 = A8（十六进制，二进制：10101000，十进制：168）。
  2. 指令2执行：读取内存A8（值=11）→ R1 = 11
  3. 指令3执行：R2 = 20（十六进制，二进制：00100000，十进制：32）。
  4. 指令4执行：R0（A8） + R1（0）（补码加法）→ R3 = A8（168）。
  5. 指令5执行：R2（20）与 R3（A8）做与运算（二进制按位与）：
    • R2二进制：0010 0000
    • R3二进制：1010 1000
    • 与运算结果：0010 0000（即十六进制20，十进制32）→ R5 = 20（十六进制）。
  6. 指令6执行：停机，程序结束。

最终寄存器5的值：\(\boldsymbol{20_{(16)}}\)（或十进制\(\boldsymbol{32}\)）。

  • d. 20A8与11A8中的A8含义是否相同
    不相同，具体区别：
  1. 20A8中的A8：是指令1（操作码2）的操作数“0A8”的后两位，对应操作码2的定义，A8是要存入寄存器0的立即数（直接赋值的数值）。
  2. 11A8中的A8：是指令2（操作码1）的操作数“1A8”的后两位，对应操作码1的定义，A8是要读取数据的内存单元地址（内存地址标识）。

简言之，前者是“数值”，后者是“内存地址”，含义完全不同。

六、

在Brooks hear给出的机器中，假设内存单元地址从00开始，请用Brooks hear给出的机器指令实现以下操作。（共3小题，每小题5分，共15分）
a. 将寄存器1与寄存器2中的值相加，存入内存单元20；
b. 将内存单元25的值，与寄存器1中的值相加，存入寄存器3；
c. 将寄存器1和寄存器2的内容互换；

  • 操作码规则
操作码 格式（操作码+3位操作数） 精准功能
1 1RXY 内存XY单元数据 → 寄存器R
2 2RXY 立即数XY → 寄存器R（直接赋值）
3 3RXY 寄存器R数据 → 内存XY单元
4 40RS 寄存器R数据 → 寄存器S（操作数固定以0开头，后两位为R、S）
5 5RST 寄存器S + 寄存器T（补码加法）→ 寄存器R
C C000 程序停机

  • 整套指令设计（地址从00开始连续分配）

  • 执行逻辑顺序：先完成 R1↔R2（功能c）→ 再完成 R1+R2→内存20（功能a）→ 最后完成 内存25+R1→R3（功能b）→ 停机

  • 整套指令设计（按a→b→c顺序，地址从00开始连续分配）

内存地址 指令内容 指令功能（对应需求） 详细说明
00 5012 功能a（R1+R2→内存20第一步） 操作码5：寄存器1 + 寄存器2（补码加法），结果存入寄存器0（临时存储加法结果）
01 3020 功能a（R1+R2→内存20第二步） 操作码3：将寄存器0（R1+R2的结果）的数据存入内存20单元（完成功能a）
02 1025 功能b（内存25+R1→R3第一步） 操作码1：将内存25单元的数据读取到寄存器0（临时存储内存25的值）
03 5301 功能b（内存25+R1→R3第二步） 操作码5：寄存器0（内存25的值） + 寄存器1，结果存入寄存器3（完成功能b）
04 4010 功能c（R1↔R2第一步） 操作码4：将寄存器1的数据存入寄存器0（R0作为临时中转，避免R1数据被覆盖）
05 4021 功能c（R1↔R2第二步） 操作码4：将寄存器2的数据存入寄存器1（此时R1变为原R2的值）
06 4002 功能c（R1↔R2第三步） 操作码4：将寄存器0（原R1）的数据存入寄存器2（完成R1↔R2互换）
07 C000 通用收尾 操作码C：程序停机
  • 验证
  1. 地址连续性：内存地址从00到07连续分配，无重复、无空缺，完全符合“内存单元地址从00开始设计一整套”的要求；
  2. 功能全覆盖（按a→b→c顺序）：
    • 地址00-01：完整实现“寄存器1与寄存器2的值相加，存入内存单元20”（功能a），先通过操作码5完成加法并暂存R0，再通过操作码3写入内存20；
    • 地址02-03：完整实现“内存单元25的值与寄存器1的值相加，存入寄存器3”（功能b），先通过操作码1读取内存25到R0，再通过操作码5完成加法并写入R3；
    • 地址04-06：完整实现“寄存器1和寄存器2的内容互换”（功能c），借助R0中转，通过3条操作码4指令完成无丢失互换；
  3. 操作码合规性：
    • 寄存器间数据传输仅使用操作码4（严格匹配“40RS”格式），无误用；
    • 补码加法仅使用操作码5，符合指令定义；
    • 内存读（操作码1）、内存写（操作码3）严格区分，无混淆；
  4. 临时寄存器合理性：全程复用R0作为临时中转寄存器，未占用业务寄存器（R1/R2/R3），避免数据覆盖，逻辑无漏洞。
  • 补充说明
    若需要给寄存器/内存赋初始值（比如测试用），可在地址00前新增指令（如地址00改为2105：立即数05存入R1；地址01改为2203：立即数03存入R2），不影响核心逻辑，仅需顺延后续指令地址即可。

七

VComputer模拟平台共有256个主存单元（分别用十六进制00~FF表示），16个通用寄存器（分别用十六进制0 ~ F表示），1个程序计数器和1个指令寄存器。
该平台的机器指令共有9条，每条指令的长度均为2个字节。指令的第1个十六进制数为操作码；指令的后3个十六进制数为操作数。VComputer的机器指令集，以及与汇编指令的对照表如下表：

操作码 操作数 汇编指令 描 述
1 RXY Load R,[XY] [R]:=[XY]
2 RXY Load R,XY [R]:=XY
3 RXY Store R,[XY] [XY]:=[R]
4 0RS Mov R,S [S]:=[R]
5 RST Add R,S,T [R]:=[S]+[T]
6 R0X Shl R,X [R]:=[R]左移X位，移位后，用0填充腾空的位
7 R00 Not R [R]:=[R]中的值按位取反
8 RXY Jmp R,XY 程序计数器[PC]:=XY, IF [R]=[R0]; else[PC]:=[PC]+2
9 000 Halt 停机

内存地址00到13的内存单元中包含以下内容：

地址 内容 地址 内容
00 10 0A 30
01 12 0B 0E
02 21 0C 52
03 6F 0D 01
04 81 0E 72
05 0A 0F 00
06 71 10 40
07 00 11 21
08 80 12 90
09 04 13 00

若程序从内存地址00开始执行，回答下列问题：（共17分）
（1）将上述Vcomputer机器指令转换为汇编程序。（5分）
（2）程序结束时，内存单元[0E]的值是多少？寄存器0、1、2的值分别又是多少？（8分）
（3）程序结束时，存放在地址10和11里的指令执行了多少次？放在地址04和05里的指令执行了多少次？（4分）

  • 前提（核心规则）
  1. VComputer每条指令占2个连续内存单元（1单元=1字节），格式为「1位十六进制操作码 + 3位十六进制操作数」；
  2. 内存单元兼具“存储指令”和“存储数据”的特性，执行Store指令修改内存单元内容时，会覆盖该地址原有指令；
  3. 程序计数器（PC）初始值=00，执行普通指令后PC+=2；跳转指令按条件修改PC；停机指令（9000）直接终止程序。
  • （1）机器指令转换为汇编程序

先拆分内存单元为完整指令（2单元=1条指令），再按指令集规则转换：

指令起始地址 机器指令（内存拼接） 操作码+操作数 汇编指令 指令说明
00 00(10)+01(12)=1012 1 012 Load 0,[12] 将内存12单元的值存入寄存器0
02 02(21)+03(6F)=216F 2 16F Load 1,6F 将立即数6F存入寄存器1
04 04(81)+05(0A)=810A 8 10A Jmp 1,0A 若R1=R0则PC=0A，否则PC=06
06 06(71)+07(00)=7100 7 100 Not 1 寄存器1的值按位取反，存回R1
08 08(80)+09(04)=8004 8 004 Jmp 0,04 若R0=R0则PC=04，否则PC=0A
0A 0A(30)+0B(0E)=300E 3 00E Store 0,[0E] 将寄存器0的值存入内存0E单元
0C 0C(52)+0D(01)=5201 5 201 Add 2,0,1 R0+R1（补码）结果存入R2
0E 0E(72)+0F(00)=7200 -> 9000 7 200 -> 9000 Not 2（被覆盖） 寄存器2的值按位取反（未执行）停机(执行)
10 10(40)+11(21)=4021 4 021 Mov 2,1（未执行） 将寄存器2的值存入寄存器1（未执行）
12 12(90)+13(00)=9000 9 000 Halt（未执行） 程序停机（未执行）
  • （2）程序结束时内存单元[0E]及寄存器0/1/2的值
  • 执行流程（关键：内存0E被覆盖为停机指令）
PC值 执行指令 操作细节 结果（寄存器/内存） PC更新后
00 Load 0,[12] 取内存12的初始值90存入R0 R0=90 02
02 Load 1,6F 立即数6F存入R1 R1=6F 04
04 Jmp 1,0A R1(6F)≠R0(90)，不跳转 - 06
06 Not 1 R1=6F（01101111）取反为90（10010000） R1=90 08
08 Jmp 0,04 R0=R0恒成立，跳转到04 - 04
04 Jmp 1,0A R1(90)=R0(90)，跳转到0A - 0A
0A Store 0,[0E] 将R0(90)存入内存0E，覆盖原内容72,变为90, 内存[0E]=90 0C
0C Add 2,0,1 R0(90)+R1(90)=180，8位补码截断为20（00100000） R2=20 0E
0E Halt（9000） 内存0E=90、0F=00拼接为停机指令9000 - 停止
  • 最终结果
  • 内存单元[0E]的值：90（十六进制）；
  • 寄存器0（R0）：90（十六进制）；
  • 寄存器1（R1）：90（十六进制）；
  • 寄存器2（R2）：20（十六进制）。
  • （3）指令执行次数统计
  • 地址10和11的指令（Mov 2,1）：程序在0E地址停机，未执行→执行次数：0次；
  • 地址04和05的指令（Jmp 1,0A）：PC=04执行1次、跳转回PC=04又执行1次→执行次数：2次。

第三次平时测试

一、判断题

判断命题正误。若命题正确填写“√”，否则填写“×”。将答案填在下表。（共6小题，每小题2分，共12分）

  1. 方程3x+6y=15有整数解。（）
  1. 算法时间复杂度是指算法中有关操作次数的多少和所占存储空间的大小，用T()表示，T(n)中的n表示问题规模的大小。（）
  1. 采用折半搜索算法从一个拥有2⁶⁴的巨大有序数列中查找其中一个特定的元素，最多只需要64次。（）
  1. 排序网络是一种并行算法，它可以同时采用多个处理机（比较器）快速地对一组数字序列进行排序。（）
  1. 在计算机中，处理英文字符信息时，不需要用二进制代码形式表示。因为，键盘上有相应的英文字符输入键。（）
  1. 在位图中，图像被看作是点的集合，每一个点叫做一个像素。而矢量图则是以指令来描述图像的。（）

二、选择题

将答案填在下表。（共6小题，每小题2分，共12分）

  1. （单选）折半搜索算法也称二分查找算法，是一种在有序数据集中查找某一特定元素的搜索算法。折半搜索要求数据集中的结点按关键字值升序或降序排列。折半搜索算法的基本原理是：首先将待查值与有序数据集的中间项进行比较，以确定待查值位于有序数据集的哪一半，然后将待查值与新的有序数据集的中间项进行比较。循环进行，直到相等为止。采用折半搜索算法在一个有10000件商品（有序排列）的超市中查找一件特定的商品，最多只需要查找的次数是（）。
    选项：
    A. 14
    B. 15
    C. 100
    D. 5000

  1. （单选）在一个计数范围是0～11的计数系统中，其模是（）。
    选项：

    A. 11
    B. 12
    C. 5
    D. 6

  1. （单选）栈是计算机中一种常用的数据结构，假设有一空栈，首先数值3A入栈，然后数值2B、8C依次入栈，随后执行一次出栈操作，最后数值9D和8E依次入栈。按栈底到栈顶的存储顺序列出当前栈内所有数据应为（）。
    选项：
    A. 8E、9D、2B、3A
    B. 8E、9D、8C、2B
    C. 3A、8C、9D、8E
    D. 3A、2B、9D、8E

  1. （单选）假设一仅含数值8A的队列，8B和2C依次入队，然后执行一次出队操作，最后数据7D和6E依次入队。那么执行这一系列的操作后从队头到队尾存储的数据依次为（）。
    选项：

    A. 6E、7D、2C、8B
    B. 6E、7D、8B、8A
    C. 8B、2C、7D、6E
    D. 8A、8B、7D、6E

  1. （单选）设某一含有4个结点的树形结构，结点中的数据分别为A3、3B、8C和D7。已知A3和8C为兄弟关系，而D7为A3的子结点。则该树中叶子结点有____，根结点是____（）。
    选项：

    A. A3、8C；3B
    B. 8C、D7；3B
    C. 8C、D7；A3
    D. 8C、3B；A3

  1. （单选）下图所示是字母“a”的6×5点阵图，其第四行的二进制编码是（）。
    选项：
    A. 101001
    B. 01110
    C. 10001
    D. 010110
列1 列2 列3 列4 列5
□ ■ ■ ■ □
□ □ □ □ ■
□ ■ ■ ■ ■
■ □ □ □ ■
■ □ □ □ ■
□ ■ ■ ■ ■

三

设数组A有7个元素，分别是23，12，96，87，62，55，17。请采用归并排序算法对该数组元素按升序进行排列。（共10分）

归并排序（升序）解题过程
已知数组

\[A=[23,12,96,87,62,55,17],\ n=7 \]

归并排序的基本思想是 分治法：先拆分，再合并排序。

一、拆分阶段

将数组不断二分，直到每个子数组只含一个元素：

\[[23,12,96,87,62,55,17] \]

\[\rightarrow [23,12,96,87]\ \ \ [62,55,17] \]

\[\rightarrow [23,12]\ [96,87]\ [62,55]\ [17] \]

\[\rightarrow [23]\ [12]\ [96]\ [87]\ [62]\ [55]\ [17] \]

二、合并阶段（按升序合并）

  1. 两两合并单元素子数组：

    \[[23] + [12] \rightarrow [12,23] \]

    \[[96] + [87] \rightarrow [87,96] \]

    \[[62] + [55] \rightarrow [55,62] \]

  2. 继续向上合并：

    \[[12,23] + [87,96] \rightarrow [12,23,87,96] \]

    \[[55,62] + [17] \rightarrow [17,55,62] \]

  3. 最终合并左右两部分：

    \[[12,23,87,96] + [17,55,62] \rightarrow [12,17,23,55,62,87,96] \]

三、排序结果

数组 \(A\) 按升序排列后的结果为：

\[[12,17,23,55,62,87,96] \]

四

假设一空栈，首先数值4B入栈，然后数值5D、8C依次入栈，随后执行2次出栈操作，最后数值9F和7A依次入栈。（共2小题，每小题6分，共12分）

  1. 请按栈底到栈顶的存储顺序列出当前栈内所有数据。
  2. 若执行出栈操作，请问取出的数据为多少？
  • 解题前提
    栈遵循后进先出（LIFO） 规则：入栈数据从栈顶添加，出栈数据从栈顶移除；栈底为最早入栈且未出栈的元素，栈顶为最后入栈的元素。
  • 步骤1：梳理栈的操作全过程
    初始状态：空栈（无任何数据）。
  1. 数值4B入栈 → 栈内（栈底→栈顶）：[4B]；
  2. 数值5D入栈 → 栈内（栈底→栈顶）：[4B, 5D]；
  3. 数值8C入栈 → 栈内（栈底→栈顶）：[4B, 5D, 8C]；
  4. 第1次出栈 → 移除栈顶的8C，栈内：[4B, 5D]；
  5. 第2次出栈 → 移除栈顶的5D，栈内：[4B]；
  6. 数值9F入栈 → 栈内（栈底→栈顶）：[4B, 9F]；
  7. 数值7A入栈 → 栈内（栈底→栈顶）：[4B, 9F, 7A]。
    1. 当前栈内数据（栈底到栈顶）
      栈底 → 栈顶：$$4B、9F、7A$$
    1. 执行出栈操作取出的数据
      栈的出栈操作从栈顶取数，当前栈顶元素为7A，因此取出的数据为$$7A$$

五

假设一仅含数值5B的队列，5C、5D和5E依次入队，然后执行一次出队操作，最后数据9F入队。（共2小题，每小题6分，共12分）

  1. 请按队头到队尾的存储顺序列出当前队列内所有数据。
  2. 若执行出队操作，请问取出的数据为多少？
  • 解题前提
    队列遵循先进先出（FIFO） 规则：入队数据从队尾添加，出队数据从队头移除；队头为最早入队且未出队的元素，队尾为最后入队的元素。
  • 步骤1：梳理队列的操作全过程
    初始状态：队列仅含数值$$5B$$（队头→队尾）：$$[5B]$$
  1. 数值$$5C$$入队 → 队头→队尾：$$[5B, 5C]$$
  2. 数值$$5D$$入队 → 队头→队尾：$$[5B, 5C, 5D]$$
  3. 数值$$5E$$入队 → 队头→队尾：$$[5B, 5C, 5D, 5E]$$
  4. 执行1次出队操作 → 移除队头的$$5B$$，队列变为：$$[5C, 5D, 5E]$$
  5. 数值$$9F$$入队 → 队头→队尾：$$[5C, 5D, 5E, 9F]$$
    1. 当前队列内数据（队头到队尾）
      队头 → 队尾：$$5C、5D、5E、9F$$
    1. 执行出队操作取出的数据
      队列的出队操作从队头取数，当前队头元素为$$5C$$，因此取出的数据为$$5C$$

六

十进制、十六进制、八进制、二进制转换的关键是将十进制数拆分为若干以2为基数的位权（位置序号从0开始，第n个位置的位权为2ⁿ），请将以下十进制数转换成对应的二进制、八进制和十六进制数的形式，二进制数填在下表中，八进制和十六进制数写在空白处。（共12分）

位权 2¹⁰ 2⁹ 2⁸ 2⁷ 2⁶ 2⁵ 2⁴ 2³ 2² 2¹ 2⁰
十进制数 1024 512 256 128 64 32 16 8 4 2 1
18（十进制数）对应的二进制数 0 0 0 1 0 0 1 0
138
345
511
1562
  • 解题前提
    十进制转二进制：按位权（2ⁿ）拆分，从最高位到最低位依次判断是否包含该位权，包含则填1，否则填0；
    二进制转八进制：从右往左每3位一组（不足补0），每组转对应八进制数；
    二进制转十六进制：从右往左每4位一组（不足补0），每组转对应十六进制数（10=A、11=B、12=C、13=D、14=E、15=F）。
  • 第一步：填写二进制数表格
位权 2¹⁰ 2⁹ 2⁸ 2⁷ 2⁶ 2⁵ 2⁴ 2³ 2² 2¹ 2⁰
十进制数 1024 512 256 128 64 32 16 8 4 2 1
18的二进制 0 0 0 0 0 0 1 0 0 1 0
138的二进制 0 0 0 1 0 0 0 1 0 1 0
345的二进制 0 0 1 0 1 0 1 1 0 0 1
511的二进制 0 1 1 1 1 1 1 1 1 1 1
1562的二进制 1 1 0 0 0 0 1 1 0 1 0
  • 第二步：各十进制数对应的八进制、十六进制

  1. 十进制18：

    • 二进制：$$00000010010$$
    • 八进制：分组（010 010）→ $$22$$
    • 十六进制：分组（0001 0010）→ $$12$$

  2. 十进制138：

    • 二进制：$$00010001010$$
    • 八进制：分组（10 001 010 → 补零为010 001 010）→ $$212$$
    • 十六进制：分组（1000 1010）→ $$8A$$

  3. 十进制345：

    • 二进制：$$00101011001$$
    • 八进制：分组（101 011 001）→ $$531$$
    • 十六进制：分组（0001 0101 1001）→ $$159$$

  4. 十进制511：

    • 二进制：$$01111111111$$
    • 八进制：分组（111 111 111）→ $$777$$
    • 十六进制：分组（0001 1111 1111）→ $$1FF$$

  5. 十进制1562：

    • 二进制：$$11000011010$$
    • 八进制：分组（110 000 110 10 → 补零为110 000 110 100 → 取前三位+中间+后三位）→ $$3032$$
    • 十六进制：分组（0110 0001 1010）→ $$61A$$

七

在链表的存储结构中，存放数据元素的存储空间记录有两部分信息，一部分用来记录数据值（数据域），另一部分用来记录该数据的后继元素所处的存储地址（指针域），如下图1(a)所示，并可用图1(c)的形式来表示单链表。图1(b)为Vcomputer机器内存的一部分，其中地址79是某单链表的首地址，请将该单链表各结点的内容填入图1(c)中。（共15分）

（注：图1(a)为“数据域|指针域”结构；图1(b)为主存地址与单元内存的对应表；图1(c)为单链表链式结构，首地址head为79）

图1(b)的主存地址与单元内存对应表如下：

地址 单元内存 地址 单元内存
70 00 78 00
71 57 79 98
72 77 7A 73
73 79 7B 68
74 7E 7C 71
75 00 7D 00
76 00 7E 78
77 45 7F 7B 
head 
↓
79 → [98 | 73] → [ | ] → [ | ] → [ | ] → [ | ] → [ | ]

解题前提

单链表每个节点包含「数据域」和「指针域」，对应两个连续的十六进制内存地址：

  • 节点起始地址（如79）的单元内容 = 数据域；
  • 起始地址的下一个地址（如79的下一个地址是7A）的单元内容 = 指针域（指向下一个节点的起始地址）；
  • 指针域为00时，链表结束。

步骤：拆解单链表节点（首地址head=79）

  1. 第一个节点：起始地址79

    • 数据域：地址79的单元内存=98；
    • 指针域：地址7A（79的下一个地址）的单元内存=73；
      → 79 → [98 | 73]

  2. 第二个节点：指针域指向73（起始地址73）

    • 数据域：地址73的单元内存=79；
    • 指针域：地址74（73的下一个地址）的单元内存=7E；
      → [79 | 7E]

  3. 第三个节点：指针域指向7E（起始地址7E）

    • 数据域：地址7E的单元内存=78；
    • 指针域：地址7F（7E的下一个地址）的单元内存=7B；
      → [78 | 7B]

  4. 第四个节点：指针域指向7B（起始地址7B）

    • 数据域：地址7B的单元内存=68；
    • 指针域：地址7C（7B的下一个地址）的单元内存=71；
      → [68 | 71]

  5. 第五个节点：指针域指向71（起始地址71）

    • 数据域：地址71的单元内存=57；
    • 指针域：地址72（71的下一个地址）的单元内存=77；
      → [57 | 77]

  6. 第六个节点：指针域指向77（起始地址77）

    • 数据域：地址77的单元内存=45；
    • 指针域：地址78（77的下一个地址）的单元内存=00（链表结束）；
      → [45 | 00]

最终单链表填充结果

head 
↓
79 → [98 | 73] → [79 | 7E] → [78 | 7B] → [68 | 71] → [57 | 77] → [45 | 00]

八

下图2所示的Vcomputer机器内存中存储了一棵首地址为E0的二叉树，每个结点的第一个单元存放的是该结点的数据，第二个单元存放的是其左子结点的地址，第三个单元存放的是其右子结点的地址。请画出这棵树（约定，若第二个单元存放的值为00，则其左子结点不存在；同理，若第三个单元存放的值为00，则其右子结点不存在）。（共15分）

（注：图2为主存地址（E0-EF）与单元内存的对应表，二叉树首地址为E0）

地址 单元内存
E0 7E
E1 E3
E2 EC
E3 8A
E4 E6
E5 00
E6 43
E7 E9
E8 00
E9 23
EA 00
EB 00
EC C6
ED 00
EE 00
EF 00

解题前提

二叉树每个节点占3个连续的十六进制内存地址：

  • 第1个地址：节点数据域；
  • 第2个地址：左子节点的起始地址（00表示无左子）；
  • 第3个地址：右子节点的起始地址（00表示无右子）；
    二叉树首地址为E0，以此为根节点逐步拆解所有节点。

步骤1：拆解所有节点的信息

节点起始地址 数据域（第1地址） 左子地址（第2地址） 右子地址（第3地址） 子节点状态
E0（根节点） E0单元=7E E1单元=E3 E2单元=EC 左子=E3，右子=EC
E3 E3单元=8A E4单元=E6 E5单元=00 左子=E6，无右子
E6 E6单元=43 E7单元=E9 E8单元=00 左子=E9，无右子
E9 E9单元=23 EA单元=00 EB单元=00 无左子、无右子（叶子节点）
EC EC单元=C6 ED单元=00 EE单元=00 无左子、无右子（叶子节点）

步骤2：二叉树结构（手写风格）

        7E  (E0)
       /   \
      /     \
    8A(E3)  C6(EC)
   /        
  /         
 43(E6)     
/           
/            
23(E9)

（补充说明：

  1. 根节点为7E（地址E0），左分支指向8A（地址E3），右分支指向C6（地址EC）；
  2. 8A（E3）仅左分支指向43（E6），无右分支；
  3. 43（E6）仅左分支指向23（E9），无右分支；
  4. 23（E9）和C6（EC）无任何子节点，为叶子节点；
  5. 所有标注的括号内为节点起始地址，无分支处代表对应子节点地址为00。）

第四次平时测试

一、判断题

判断命题正误。若命题正确填写“√”，否则填写“×”。将答案填在下表。（共9小题，每小题2分，共18分）

  1. 连续数学是离散数学的基础，因此，要学好离散数学，首先要学好连续数学。（）
  1. 血缘关系不是等价关系。（）
  1. 语言与数学模型是一一对应的关系，一种语言只能由不同的文法产生，也只能由一种自动机识别。（）
  1. 迭代程序都可以转换为与它等价的递归程序，反之亦然。（）
  1. 一般认为，《周髀算经》中的“盖天学说”是我国古代学者惟一的公理化方法尝试。（）
  1. 哥德尔的“不完备性定理”指出：如果一个形式的数学理论是足够复杂的，而且它是无矛盾的，那么在这一理论必存在一个命题，而这一命题在这一理论中是既不能证明，也不能否证。（）
  1. 若能构造实现加法运算的机器，就一定可以构造出能实现其他运算的机器。（）
  1. 计算机科学家和数学家都是科学家，都关心事物的本质特征，没有什么区别。（）
  1. 形式化方法是提高软件系统，特别是安全至上的软件系统的安全性与可靠性的重要手段。（）

二、判定条件题

判定下列句子关注的是必要条件，充分条件，或充分必要条件，或既不是充分条件也不是必要条件，将题号填写在下表中。（共9小题，每小题2分，共18分）

  1. 欧拉对任一连通无向图是否存在“欧拉回路”的判定。
  1. 兼容并包。
  1. 新上项目的讨论。
  1. 让爱包容。
  1. 外语水平是优秀人才的什么条件。
  1. 良好的品德是成为学术大师的什么条件。
  1. 有容乃大。
  1. 伟大的人格是成为伟大科学家的什么条件。
  1. 掌握布尔代数的基础知识是完成复杂数字逻辑电路设计的什么条件。

三、选择题

将答案填在下表。（共6小题，每小题2分，共12分）

  1. （多选）在对待数学的问题上，数学家和计算机科学家侧重点分别是（）。
    选项：
    A. 数学家关心的是“是什么（What is it）”的问题，不是“怎么做（How to do it）”的问题
    B. 计算机科学家关心的不是“是什么（What is it）”的问题，而是“怎么做（How to do it）”的问题
    C. 数学家关心的不是“是什么（What is it）”的问题，而是“怎么做（How to do it）”的问题
    D. 计算机科学家不仅要知道“是什么（What is it）”的问题，而且要解决“怎么做（How to do it）”的问题
  1. （单选）计算学常采用分层抽象的方法降低和控制系统的复杂程度，而分层抽象背后的原理是数学中的等价关系。请指出下列满足等价关系的是（）。
    选项：
    A. 血缘关系
    B. 并发关系
    C. 朋友关系
    D. 同姓关系
  1. （单选）“充分条件，必要条件”是征服数学的关键，只要能够清楚的分辨，就能克服数学。遗憾的是，即使顶尖的高手，在辩论中，也常搞混这两个概念。外语水平是优秀人才的什么条件（）。
    选项：
    A. 充分条件
    B. 必要条件
    C. 既不是充分条件，也不是必要条件
    D. 充分必要条件
  1. （单选）求阿克曼函数的值A(1,1)=____（）。
    选项：
    A. 1
    B. 2
    C. 3
    D. 5

  1. （单选）笛卡儿积具有重要的理论价值，可以说，事物之间所有的关联都在笛卡儿积之中。然而，人与机器对笛卡儿积产生的“组合爆炸”问题是无法进行处理的。因此，尽管笛卡儿积“完美无缺”，但却无任何实际的应用价值。因此，在实际工作中，我们还要充分运用与集合相关的函数、关系、定义等数学工具，将注意力放在事物之间具有实质性关联的方面，最终控制和降低系统的复杂性。集合A₁，A₂，…，Aₙ的乘积一般用法国数学家笛卡儿（Rene Descartes）的名字命名，即笛卡儿积。下列有关正确的是:

    A. \(A_1 \times A_2 \times \dots \times A_n = \{ (a_1, a_2, \dots, a_n) \mid a_i \in A_i,\ i=1,2,\dots,n \}\)

    B. \(A_1 \times A_2 \times \dots \times A_n\) 的结果是一个有序 \(n\) 元组的集合，集合中的元素个数为 \(\prod_{i=1}^{n}|A_i|\)。假如 \(|A_i|=10^4\ (i=1,2,\dots,n)\)，\(n=10^4\)，那么集合中有 \((10^4)^{10^4}\) 个元素

    C. 若集合 \(A\) 有 \(n\) 个元素，集合 \(B\) 有 \(m\) 个元素，\(A \times B\) 有 \(n^m\) 个元素

    D. 若 \(A=\{1,2,3\}\)，\(B=\{a,b\}\)，\(A \times B=\{ (1,a), (1,b), (2,a), (2,b), (3,a), (3,b) \}\)

  1. （单选）下面是采用蒙特卡罗方法编写的计算圆周率π的值Raptor程序。根据你的理解，请补全空白处（1）的代码（）。
    （程序说明：生成x、y为[0,1)之间的随机数，sum统计落在单位圆内的随机点个数，最终P=4*sum/n得到π的近似值）
Start（功能：生成随机点估算π）
  ↓
提示"Enter the total number of random points" → 获取n（随机点总数）
  ↓
初始化：i ← 0（计数用）、sum ← 0（统计单位圆内的点数）
  ↓
Loop（循环）
  ↓
判断：i ≥ n？
  → Yes:
        ↓
        计算P ← 4 * sum / n（用圆内点比例算π的近似值）
        ↓
        输出P
        ↓
        End
  → No:
        ↓
        生成x ← 0-1之间的随机数
        ↓
        生成y ← 0-1之间的随机数
        ↓
        判断：x² + y² ≤ 1？（是否落在单位圆内）
            → Yes: sum ← sum + 1
            → No: 无操作
        ↓
        i ← i + 1
        ↓
        回到Loop

选项：
A. xx+yy=1
B. xx+yy≤1
C. xx+yy≥1
D. xx+yy==1

四、集合运算题

已知集合A={a,b,c,d}，B={1,2,3}，求A∪B和A×B的值。（共2小题，每小题5分，共10分）

  • 解题前提
  1. 并集（\(\boldsymbol{A\cup B}\)）：由所有属于集合\(A\) 或 属于集合\(B\)的元素组成的集合，元素具有互异性（无重复）。
  2. 笛卡尔积（\(\boldsymbol{A\times B}\)）：由所有第一个元素属于\(A\)、第二个元素属于\(B\)的有序对\((x,y)\)组成的集合，公式为 \(A\times B=\{(x,y)|x\in A,y\in B\}\)。
  • 已知条件
    \(A=\{a,b,c,d\}\)，\(B=\{1,2,3\}\)，两个集合无公共元素。
    1. 计算\(\boldsymbol{A\cup B}\)
      直接合并两个集合的所有元素，去除重复（本题无重复）：

\[A\cup B=\{a,b,c,d,1,2,3\} \]

    1. 计算\(\boldsymbol{A\times B}\)
      遍历\(A\)中每个元素与\(B\)中每个元素组成有序对，共\(4\times3=12\)个有序对：

\[\begin{align} A\times B =&\{(a,1),(a,2),(a,3), \\ &(b,1),(b,2),(b,3), \\ &(c,1),(c,2),(c,3), \\ &(d,1),(d,2),(d,3)\} \end{align} \]

五、证明题

证明整数N上的模2的同余关系R为等价关系。（共12分）

  • 证明：整数集\(\mathbb{Z}\)上的模2同余关系\(R\)为等价关系
  1. 明确关系定义
    设整数集为\(\mathbb{Z}\)，模2的同余关系\(R\)定义为：

\[\forall a,b\in\mathbb{Z},\ aRb \iff 2\mid (a-b) \]

（即\(a\)与\(b\)除以2的余数相同，记为\(a\equiv b\pmod{2}\)）

等价关系需满足自反性、对称性、传递性三个条件，逐一证明如下。

  1. 证明自反性
    自反性定义：\(\forall a\in\mathbb{Z}\)，有\(aRa\)。
    对任意整数\(a\)，计算\(a-a=0\)。
    因为\(2\mid 0\)（0能被任何非零整数整除），所以\(2\mid (a-a)\)。
    根据关系定义，\(aRa\)成立。
    因此，\(R\)满足自反性。
  1. 证明对称性
    对称性定义：\(\forall a,b\in\mathbb{Z}\)，若\(aRb\)，则\(bRa\)。
    假设\(aRb\)，根据定义有\(2\mid (a-b)\)，即存在整数\(k\)，使得

\[a-b=2k \]

变形可得 \(b-a=-(a-b)=-2k=2(-k)\)。
因为\(k\)是整数，所以\(-k\)也是整数，因此\(2\mid (b-a)\)。
根据关系定义，\(bRa\)成立。
因此，\(R\)满足对称性。

  1. 证明传递性
    传递性定义：\(\forall a,b,c\in\mathbb{Z}\)，若\(aRb\)且\(bRc\)，则\(aRc\)。
    假设\(aRb\)且\(bRc\)，根据定义有：

\[2\mid (a-b)\ \text{且}\ 2\mid (b-c) \]

即存在整数\(k,m\)，使得

\[a-b=2k,\quad b-c=2m \]

将两式相加：

\[(a-b)+(b-c)=2k+2m \]

化简得 \(a-c=2(k+m)\)。
因为\(k,m\)是整数，所以\(k+m\)也是整数，因此\(2\mid (a-c)\)。
根据关系定义，\(aRc\)成立。
因此，\(R\)满足传递性。

  1. 结论
    模2的同余关系\(R\)满足自反性、对称性、传递性，因此\(R\)是整数集\(\mathbb{Z}\)上的等价关系。

六、阿克曼函数题

阿克曼函数的递归定义如下：

\[A(m,n)= \begin{cases} n + 1 & 若\ m = 0 \\ A(m-1,1) & 若\ n = 0 \\ A(m-1,A(m,n-1)) & 若\ m,n>0 \end{cases} \]

请求出A(1,1)，A(2,1)的值。（共2小题，每小题6分，共12分）

解题前提
阿克曼函数的递归定义：

\[A(m,n)= \begin{cases} n + 1 & 若\ m = 0 \\ A(m-1,1) & 若\ n = 0 \\ A(m-1,A(m,n-1)) & 若\ m,n>0 \end{cases} \]

计算时需从内向外逐层展开，优先代入符合条件的分支。

  1. 计算\(\boldsymbol{A(1,1)}\)
    已知 \(m=1>0\)，\(n=1>0\)，代入第三个分支：

\[A(1,1)=A(0,A(1,0)) \]

第一步：计算内层 \(A(1,0)\)
\(m=1>0\)，\(n=0\)，代入第二个分支：

\[A(1,0)=A(0,1) \]

\(m=0\)，代入第一个分支：

\[A(0,1)=1+1=2 \]

因此 \(A(1,0)=2\)。

第二步：回代计算 \(A(1,1)\)

\[A(1,1)=A(0,2) \]

\(m=0\)，代入第一个分支：

\[A(0,2)=2+1=3 \]

最终：\(\boldsymbol{A(1,1)=3}\)

  1. 计算\(\boldsymbol{A(2,1)}\)
    已知 \(m=2>0\)，\(n=1>0\)，代入第三个分支：

\[A(2,1)=A(1,A(2,0)) \]

第一步：计算内层 \(A(2,0)\)
\(m=2>0\)，\(n=0\)，代入第二个分支：

\[A(2,0)=A(1,1) \]

由上一步结果得 \(A(1,1)=3\)，因此 \(A(2,0)=3\)。

第二步：回代得 \(A(2,1)=A(1,3)\)
计算 \(A(1,3)\)，\(m=1>0\)，\(n=3>0\)，代入第三个分支：

\[A(1,3)=A(0,A(1,2)) \]

第三步：计算 \(A(1,2)\)
\(m=1>0\)，\(n=2>0\)，代入第三个分支：

\[A(1,2)=A(0,A(1,1))=A(0,3) \]

\(m=0\)，代入第一个分支：

\[A(0,3)=3+1=4 \]

因此 \(A(1,2)=4\)。

第四步：回代计算 \(A(1,3)\)

\[A(1,3)=A(0,4)=4+1=5 \]

最终：\(\boldsymbol{A(2,1)=5}\)

七、蒙特卡洛方法程序填空题

采用蒙特卡洛（Monte Carlo）方法，计算1≤x≤2区间内曲线\(y=2\sqrt{x}\)下的近似面积（该区间内曲线与x轴、y轴所围成的区域的面积），请将下面RAPTOR程序的空白处补充完整。（共3空，每空6分，共18分）

程序流程：

Start（功能：蒙特卡罗模拟近似求曲线f(x)=2√x(1≤x≤2)下的面积）
  ↓
提示"Enter the total number of random points:" → 获取n（随机点总数）
  ↓
初始化：Area ← 0、Counter ← 0（统计曲线下点数）、i ← 0（计数用）
  ↓
Loop（循环）
  ↓
判断：i > n？
  → Yes:
        ↓
        计算Area ← 2×√2×Counter / n（用点比例算曲线下面积）
        ↓
        输出Area
        ↓
        End
  → No:
        ↓
        生成x ← random + 1（生成1~2之间的随机x坐标）
        ↓
        生成 (1)(y ← random × 2√2(生成0~2√2之间的随机y坐标))
        ↓
        (2)判断：y ≤ 2√x？（判断随机点是否在曲线下方）
            → Yes: Counter ← Counter + 1
            → No: 无操作
        ↓
        (3)i ← i + 1
        ↓
        回到Loop

第五次平时测试

一．判断题

判断命题正误。若命题正确则在下表的题目标号下填“√”，否则在题目标号下填写“×”。（共5小题，每小题2分，共10分）

  1. 反向传播算法（Backpropagation）是目前用来训练神经网络的最常用且最有效的算法，其主要思想是计算估计值与实际值之间的误差，并将该误差从输出层向隐藏层、输入层反向传播，然后根据误差调整各种模型参数。（）
  1. 在朴素贝叶斯分类器中引入“拉普拉斯平滑”方法是为了实现概率的归一化。（）
  1. 最大梯度下降法是一种可以快速找到函数极值点的方法，其原理是沿着梯度向量相反的方向，梯度减少最快，因此更加容易找到函数的最小值。该方法只能用于线性回归模型中。（）
  1. 单层感知器能够实现逻辑与运算、逻辑或运算和逻辑非运算，但不能实现逻辑异或运算。（）
  1. 理论上，根据概率的公理系统，即概率的非负性、归一性和可加性这三条公理，可以派生出概率理论的一系列重要性质。（）

二．选择题

将答案填在下表。（共5小题，每小题2分，共10分）

  1. （单选）已知 \(P(A)=0.5,\ P(B)=0.6,\ P(A\cap B)=0.2\)，则 \(P(A\cup B)=（）\)（共2分）
    选项：
    A. 1
    B. 0.8
    C. 0.9
    D. 0
  1. （单选）\(f(x)=x^2-2\ln x\) 的最小值为（）（共2分）
    选项：
    A. 1
    B. e
    C. 1/e
    D. 2
  1. （单选）设 \(f(x,y)=x^2+3xy+y-1\)，则 \(\frac{\partial f}{\partial x}\) 和 \(\frac{\partial f}{\partial y}\) 在点 \((4,3)\) 的值分别为（）（共2分）
    选项：
    A. 17, 12
    B. 17, 13
    C. 18, 13
    D. 18, 12
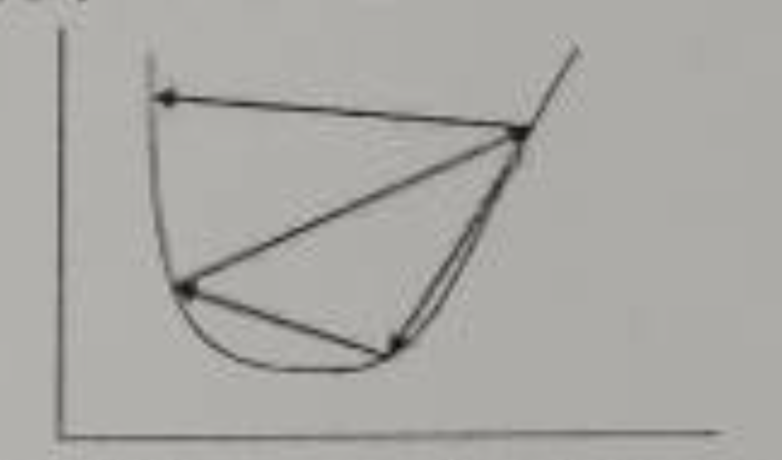
  1. （单选）在神经网络模型训练中，造成如图所示现象的原因是（）（共2分）
    （说明：图为训练过程中损失波动大的曲线）
    选项：
    A. 模型参数过小
    B. 模型参数过大
    C. 学习率过小
    D. 学习率过大
    img
  1. （多选）激活函数（Activation functions）对于神经网络模型学习、理解复杂和非线性的函数来说具有十分重要的作用，因为它将非线性特性引入到我们的网络中。下列属于激活函数的是（）（共2分）
    选项：
    A. \(f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}\)
    B. \(f(x)=\max(0,x)\)
    C. \(f(x)=x\)
    D. \(f(x)=\frac{1}{1+e^{-x}}\)

三．概率计算题

重复投掷一颗均匀的骰子，设事件\(A\)，\(B\)定义为：\(A=\)“掷出的点数能被2整除”，\(B=\)“掷出的点数能被3整除”，试利用条件概率公式求\(A\)在\(B\)之前发生的概率。（共10分）

（提示：利用条件概率公式，计算$ P(A|\overline{B})=\frac{P(A\cap \overline{B})}{P(\overline{B})} $）

解题过程

定义事件

\(A={2,4,6}\)（点数能被 2 整除）
\(B={3,6}\)（点数能被 3 整除）

单次掷骰为等可能事件，样本空间大小为 6。

理解

“\(A\) 在 \(B\) 之前发生”是指：在重复掷骰的过程中，第一次出现 \(A\) 或 \(B\) 时，出现的是 \(A\) 而不是 \(B\)。

因此：

  • \(A\) 赢：\(A\) 发生且 \(B\) 未发生，即 \(A\cap\overline B\)
  • \(B\) 赢：\(B\) 发生且 \(A\) 未发生，即 \(B\cap\overline A\)

若 \(A\) 与 \(B\) 同时发生，或二者均未发生，则不能判定胜负，只会延迟试验。

计算独占事件的概率

\(\overline B={1,2,4,5}\)，
\(A\cap\overline B={2,4}\)，

\(P(A\cap\overline B)=\frac{2}{6}\)。

\(\overline A={1,3,5}\)，
\(B\cap\overline A={3}\)，

\(P(B\cap\overline A)=\frac{1}{6}\)。

计算 \(A\) 在 \(B\) 之前发生的概率

\(P(A\text{ 在 }B\text{ 之前})=\dfrac{P(A\cap\overline B)}{P(A\cap\overline B)+P(B\cap\overline A)}\)

\(=\dfrac{\frac{2}{6}}{\frac{2}{6}+\frac{1}{6}}=\frac{2}{3}\)。

结论

\(P(A\text{ 在 }B\text{ 之前发生})=\frac{2}{3}\)

四．贝叶斯定理应用题

有甲、乙、丙三名射手，射中靶的概率分别为 \(0.6\), \(0.5\), \(0.4\)。某次三人同时射击，有两弹中靶，试根据贝叶斯定理分析丙中靶的可能性大还是不中靶的可能性大。（共15分）

（提示：用事件 \(A\) 表示“三人同时射击，有两弹中靶”，事件 \(B_1\) 表示“丙中靶”，事件 \(B_2\) 表示“丙不中靶”，利用贝叶斯公式计算 \(P(B_1|A)\) 和 \(P(B_2|A)\)，并比较二者大小。）

设事件

\[A={\text{三人射击，有两弹中靶}} \]

\[B_1={\text{丙中靶}},\quad B_2={\text{丙不中靶}} \]

已知命中概率

\[P(\text{甲中})=0.6,\quad P(\text{乙中})=0.5,\quad P(\text{丙中})=0.4 \]

\(P(A\mid B_1)\) 的计算

\[B_1={\text{丙中靶}} \]

在 \(B_1\) 已发生的条件下，要使事件 \(A\)（三人中恰有两人中靶）发生，
必须且只能出现以下两种互斥情况之一：

① 甲中、乙不中
② 甲不中、乙中

因此

\[P(A\mid B_1) =P(\text{甲中,乙不中})+P(\text{甲不中,乙中}) \]

\[=0.6(1-0.5)+(1-0.6)0.5 \]

\[=0.3+0.2=0.5 \]

\(P(A\mid B_2)\) 的计算

\[B_2={\text{丙不中靶}} \]

在 \(B_2\) 已发生的条件下，要使事件 \(A\)（三人中恰有两人中靶）发生，
只能出现一种情况：

甲中且乙中

因此

\[P(A\mid B_2)=P(\text{甲中,乙中}) \]

\[=0.6\times0.5=0.3 \]

先验概率

\[P(B_1)=0.4,\quad P(B_2)=0.6 \]

由全概率公式

\[P(A)=P(A\mid B_1)P(B_1)+P(A\mid B_2)P(B_2) \]

\[=0.5\times0.4+0.3\times0.6=0.2+0.18=0.38 \]

由贝叶斯公式

\[P(B_1\mid A)=\frac{P(A\mid B_1)P(B_1)}{P(A)} =\frac{0.5\times0.4}{0.38}=\frac{0.20}{0.38}\approx0.526 \]

\[P(B_2\mid A)=\frac{P(A\mid B_2)P(B_2)}{P(A)} =\frac{0.3\times0.6}{0.38}=\frac{0.18}{0.38}\approx0.474 \]

结论

\[P(B_1\mid A)>P(B_2\mid A) \]

丙中靶的可能性更大

五．朴素贝叶斯分类题

表1给出了一组关于不同特征西瓜质量分析的数据集，包含4个训练样本，1个测试样本，2个类标（好瓜、坏瓜）。请利用朴素贝叶斯分类器对测试样本进行类标划分，并给出划分过程。计算过程中会用到表2中的条件概率。（15分）

表1 一组不同特征西瓜质量分析的数据集

序号 训练样本（颜色、声音、纹理） 类标（西瓜类型）
1 深绿/清脆/深纹 好瓜
2 浅绿/沉闷/浅纹 好瓜
3 深绿/适中/浅纹 坏瓜
4 浅绿/沉闷/浅纹 坏瓜
5 测试样本：浅绿/清脆/浅纹 ？

表2 各条件概率

单词 P(特征|好瓜) P(特征|坏瓜)
深绿
清脆
浅纹

① 先验概率

训练样本共 4 个，其中好瓜 2 个，坏瓜 2 个：

\[P(\text{好瓜})=\frac{2}{4}=0.5,\quad P(\text{坏瓜})=\frac{2}{4}=0.5 \]

② 条件概率统计（表2补全）

特征 \(P(\text{特征}\mid\text{好瓜})\) \(P(\text{特征}\mid\text{坏瓜})\)
深绿 \(\frac{1}{2}\) \(\frac{1}{2}\)
清脆 \(\frac{1}{2}\) \(0\)
浅纹 \(\frac{1}{2}\) \(1\)

③ 后验概率计算（不归一化）

测试样本：浅绿 / 清脆 / 浅纹

\[P(\text{好瓜}|\text{样本}) \propto 0.5 \times \frac12 \times \frac12 \times \frac12 = \frac{1}{16} \]

\[P(\text{坏瓜}|\text{样本}) \propto 0.5 \times \frac12 \times 0 \times 1 = 0 \]

④ 分类结论

\[P(\text{好瓜}|\text{样本}) > P(\text{坏瓜}|\text{样本}) \]

测试样本判定为：好瓜

六．函数求导题

求

\[\tanh(x)=\frac{\sinh(x)}{\cosh(x)}=\frac{e^x-e^{-x}}{e^x+e^{-x}} \]

的导数。

一、用到的求导公式

\[\frac{d}{dx}e^x=e^x,\qquad \frac{d}{dx}e^{-x}=-e^{-x} \]

商的求导法则：

\[\left(\frac{u}{v}\right)'=\frac{u'v-uv'}{v^2} \]

二、原函数表示

\[\tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} \]

设

\[u=e^x-e^{-x},\quad v=e^x+e^{-x} \]

三、分别求导

\[u'=e^x+e^{-x},\quad v'=e^x-e^{-x} \]

四、应用商的求导法则

\[\tanh'(x) =\frac{(e^x+e^{-x})(e^x+e^{-x})-(e^x-e^{-x})(e^x-e^{-x})}{(e^x+e^{-x})^2} \]

五、化简

\[=\frac{(e^x+e^{-x})^2-(e^x-e^{-x})^2}{(e^x+e^{-x})^2} \]

\[=\frac{4}{(e^x+e^{-x})^2} \]

六、最终结果

\[\boxed{\tanh'(x)=\frac{1}{\cosh^2(x)}=1-\tanh^2(x)} \]

七．梯度下降法分析题

利用最大梯度下降法求解函数 \(y=x^2\) 的最小值，设初始状态为 \(x_0=5\)，学习率 \(\eta=1\)，求解过程中会出现什么问题？为什么？（共15分）

① 最大梯度下降法说明

最大梯度下降法（Gradient Descent）是一种迭代优化方法，其基本更新公式为

\[x_{k+1}=x_k-\eta,\nabla y(x_k) \]

其中 \(\eta\) 为学习率，\(\nabla y(x)\) 为目标函数在 \(x\) 处的梯度。

② 本题目标函数与梯度

\[y=x^2,\qquad \nabla y(x)=\frac{dy}{dx}=2x \]

③ 按给定参数进行迭代

初始值：\(x_0=5,\ \eta=1\)

第 1 次迭代：

\[x_1=x_0-1\cdot 2x_0=5-10=-5 \]

第 2 次迭代：

\[x_2=x_1-1\cdot 2x_1=-5-(-10)=5 \]

④ 迭代现象

\[x_0=5 \rightarrow x_1=-5 \rightarrow x_2=5 \rightarrow \cdots \]

迭代在 \(5\) 与 \(-5\) 之间来回震荡，无法收敛到最小值 \(x=0\)。

⑤ 出现的问题及原因

  • 问题：梯度下降过程不收敛，发生震荡。
  • 原因：学习率 \(\eta=1\) 过大，每一步更新跨越最小值点，导致反复越过最优解而无法逼近。

对于函数 \(y=x^2\)，梯度下降法要收敛需满足

\[0<\eta<1 \]

八．单层感知器迭代题

（共10分）在讲义例16“用单层感知器求逻辑‘与’运算”中，学习率选取为

\[\eta = 0.02 \]

第一次迭代后得到的结果为

\[w_1 = w_2 = 0.05,\quad b = 0 \]

请分析第二次迭代过程，回答以下问题：

（1）第二次迭代输入

\[x_1^{(2)} = 0,\quad x_2^{(2)} = 1 \]

此时逻辑真值

\[y^{(2)} \]

和输出值

\[\overline{y}^{(2)} \]

各是多少？（2分）

（2）根据迭代公式

\[w_i := w_i - \eta \left( \overline{y}^{(j)} - y^{(j)} \right) x_i^{(j)}, \quad (j = 2) \]

求

\[w_1,\; w_2 \]

迭代后的更新值；（4分）

（3）根据迭代公式

\[b := b - \eta \left( \overline{y}^{(j)} - y^{(j)} \right), \quad (j = 2) \]

求

\[b \]

迭代后的更新值；（2分）

（4）此时是否有必要进行下一轮迭代？为什么？
（提示：判断迭代是否收敛，即比较更新前后的

\[w_1,\; w_2,\; b \]

是否保持不变）（2分）

（1）\(y^{(2)}\) 与 \(\overline{y}^{(2)}\)

逻辑“与”运算中

\[(0,1);\Rightarrow; y^{(2)}=0 \]

加权和：

\[net=0.05\times0+0.05\times1+0=0.05>0 \]

因此

\[\overline{y}^{(2)}=1 \]

（2）权值更新

误差项：

\[\overline{y}^{(2)}-y^{(2)}=1-0=1 \]

\[w_1^{new} =0.05-0.02\times1\times0 =0.05 \]

\[w_2^{new} =0.05-0.02\times1\times1 =0.03 \]

（3）偏置更新

\[b^{new} =0-0.02\times1 =-0.02 \]

（4）是否需要继续迭代

\[(w_1,w_2,b);:;(0.05,0.05,0);\rightarrow;(0.05,0.03,-0.02) \]

更新前后参数发生变化，尚未收敛，需要继续下一轮迭代。

九．学习体会题

经过三个月左右的学习，相信同学们已经感受到本课程作为国家一流课程的许多独到之处。请结合对本章“计算学科中的统计学方法”的学习，分享自己的学习体会。（共5分）

结合《计算思维与数学建模》课程中“计算学科中的统计学方法”这一章的学习，我对计算学科的认识有了明显深化。统计学方法并不是独立于计算机科学之外的工具，而是贯穿于数据分析、算法设计、系统评估与决策优化等核心环节，是计算思维的重要组成部分。本章通过概率、随机变量、贝叶斯方法等内容，帮助我理解了计算问题中“不确定性如何被建模和处理”，体现了计算学科从数据出发、以模型支撑决策的思想。

作为网络工程专业的学生，这一章的内容与实际专业学习联系尤为紧密。网络流量分析、异常检测、可靠性评估和性能预测等问题，本质上都依赖统计建模与概率分析方法。本章让我意识到，统计学不仅服务于理论分析，也直接支撑工程实践，是连接数学基础与工程应用的重要桥梁。

总体来看，本课程通过引入统计学视角，强化了我对计算学科“抽象—建模—分析”这一核心思维路径的理解，也让我更加清晰地认识到计算思维在复杂系统和现实问题中的方法论价值，体现了国家一流课程在学科整合与能力培养方面的独到之处。

posted @ 2025-12-28 18:06  LFmin  阅读(28)  评论(0)    收藏  举报