单调栈练习(下)笔记
题目二316. 去除重复字母
- 题意:给定一个字符串,删除其中重复的字母,使得剩下的字符串由最小的字典序排列。
要求:每种字母保留一个
-
思路:
如果我们维护一个严格大压小的单调栈,那么这个栈从栈底部到栈顶部构成的字符串一定是字典序最小的。 -
为什么?
因为我们每一次处理一个字母,都要看它是否大于栈顶的字母,如果大于,说明栈顶的字母可以被弹出,因为它后面都不可能再出现在栈顶的字母的右侧。
- 如何维护单调栈?
- 先看这个字母是否入过栈,如果入过了,就跳过它
怎么看它有没有过呢?用一个标记数组来解决 - 如果当前字母的字典序是小于栈顶的字母,那么我们就把栈顶弹出
然后思考,就这样弹出会有问题吗? 会!
题目要求我们每种字符保留一种,如果它恰好是这种字母的独苗呢?是不是就不能弹出了?
- 如何解决?
我们用一张表来记录每种字母出现的次数,每一次处理它,不管有没有弹出,我们都要把它的词频减一。
如果词频为0,说明这个字母已经被弹出了,我们就不能再弹出它。
- 代码
class Solution {
private static final int maxn = 26;// 26个字母,所以数组大小为26
private static char[] stack = new char[maxn];
private static int[] cnts = new int[maxn];
private static boolean[] enter = new boolean[maxn];
private static int r;
public String removeDuplicateLetters(String s) {
char[] cha = s.toCharArray();// 字符串转字符数组,方便处理
r = 0;
Arrays.fill(cnts, 0);//初始化词频数组
Arrays.fill(enter, false);
for (char cur : cha) {
cnts[cur - 'a']++;//统计词频
}
for (char cur : cha) {
if (!enter[cur - 'a']) {
while (r > 0 && stack[r - 1] > cur && cnts[stack[r - 1] - 'a'] > 0) {
enter[stack[r - 1] - 'a'] = false;// 这里它出栈了,就要改变标记,代表它没有入过栈
r--;// 弹出栈顶
}
stack[r++] = cur;
enter[cur - 'a'] = true;
}
cnts[cur - 'a']--;//不管是否弹出, 走过了它,它的词频减一
}
return String.valueOf(stack, 0, r);// char数组转字符串
}
}
题目四:统计全是1的矩形
给你一个 m x n 的二进制矩阵 mat ,请你返回有多少个 子矩形 的元素全部都是 1 。
示例 1:
输入:mat =
[ [1,0,1],
[1,1,0],
[1,1,0]]
输出:13
解释:
有 6 个 1x1 的矩形。
有 2 个 1x2 的矩形。
有 3 个 2x1 的矩形。
有 1 个 2x2 的矩形。
有 1 个 3x1 的矩形。
矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13 。
示例 2:
输入:mat =
[
[0,1,1,0],
[0,1,1,1],
[1,1,1,0]]
输出:24
解释:
有 8 个 1x1 的子矩形。
有 5 个 1x2 的子矩形。
有 2 个 1x3 的子矩形。
有 4 个 2x1 的子矩形。
有 2 个 2x2 的子矩形。
有 2 个 3x1 的子矩形。
有 1 个 3x2 的子矩形。
矩形数目总共 = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24 。
图解思路
还是维护一个严格大压小的单调栈
- 先回顾我们做一维直方图的情况,我们以每一行做底,计算每行矩形高
- 先看这个例子:
[4, 9, 7, 2]
这是它的直方图样式
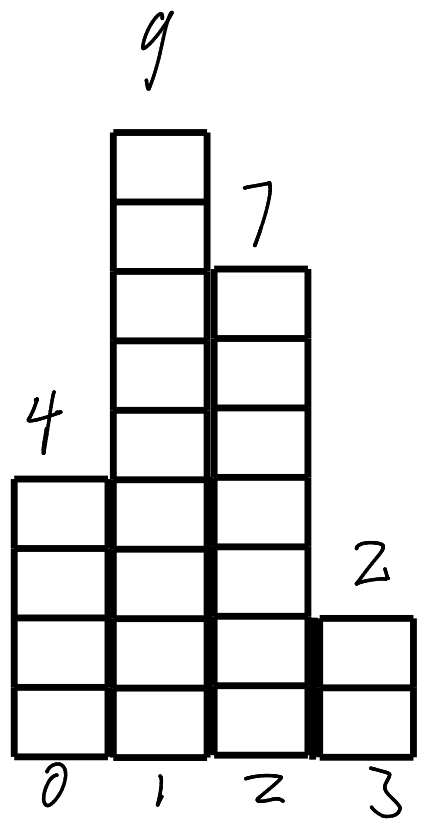
2. 我们找当前左右离它最近的比它小的两个数的较大值max,然后先数这个较大值加1到它本身就几个矩形。
也就是说我们只算max + 1 到height[cur]这个范围高度的矩形,在当前的范围上有多少个,就是矩形数目。
- 图解:
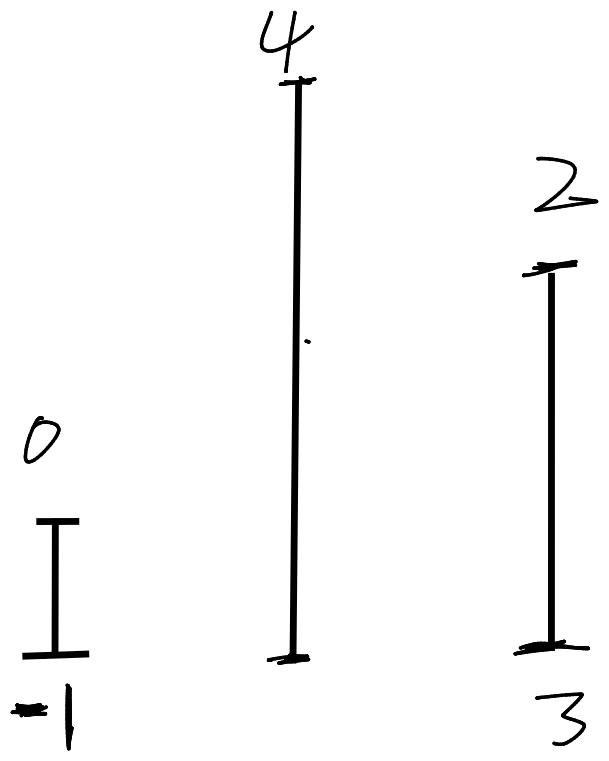
分析
我们先让0位置的4入栈,然后它左边离它最近且比它小的数是-1位置的0,右边离它最近且比它小的数是3位置的2。
也就是说我们只数高度<= 4 且> 2 的矩形
我们先数以3, 4 为高的矩形,在当前的范围(-1 到 3)上有多少个,就是:
4为高的 : 0-0(0到0), 0-1, 0-2, 1-1, 1-2, 2-2
我们观察它和我们的长度和数量有什么联系
当前范围的长度: len = right - left - 1 =(3 - (-1)) -1 = 3;
当前范围4高度的矩形数量: cnt = (3 * (3 + 1)) / 2 = 6;
3为高的 : 0-0, 0-1,0-2, 1-1, 1-2, 2-2
当前范围的长度: len = right - left - 1 =(3 - (-1)) -1 = 3;
当前范围4高度的矩形数量: cnt = (3 * (3 + 1)) / 2 = 6;
总共十二个矩形。
我们发现,刚才发现四的区域是不是刚好可以向下兼容,同时也是三的区域啊?
很容易理解,这块区域盖四层高的都没问题,那么盖三层高的自然也行。
刚刚以0位置的4为中心,它一共包括了几种矩形啊?
两种嘛,3 和 4, 怎么得的?
4(当前高度height[cur]) - 2[左右较大值] = 2;
于是以四为中心的区域总共有的矩形就是:
2 * 6 = 12个
我们抽象化一下就是
(height[cur] - max) * (len) * (len + 1) /2
为什么我们不用算1, 2那些矩形呢?它们明明也被兼容了呀?
因为在后面会被其他矩形覆盖掉,所以不用算。
这里自己往后推算会发现,我们在处理3位置的二的时候,它处理了。
代码
class Solution {
private static int[] height = new int[151];
private static int[] stack = new int[151];
private static int n, m;
private static int r;
public int numSubmat(int[][] mat) {
Arrays.fill(height, 0);
n = mat.length;
m = mat[0].length;
int ans = 0;
for (int i = 0; i < n; i ++) {
for (int j = 0; j < m; j ++) {
height[j] = mat[i][j] == 0 ? 0 : (height[j] + 1);
}
ans += compute(m);
}
return ans;
}
private static int compute(int m) {
r = 0;
int ans = 0;
for (int i = 0, left, len, bottom; i < m; i ++) {
while (r > 0 && height[stack[r - 1]] >= height[i]) {
int cur = stack[--r];
if (height[cur] > height[i]) {
left = r == 0 ? -1: stack[r - 1] ;
len = i - left - 1;
bottom = Math.max(height[i], left == -1 ? 0 : height[left]);
ans += (height[cur] - bottom) * len * (len + 1) / 2;
}
}
stack[r++] = i;
}
while (r > 0) {
int cur = stack[--r];
int left = r == 0 ? -1: stack[r - 1] ;
int len = m - left - 1;
int down = left == -1 ? 0 : height[left];
ans += (height[cur] - down) * len * (len + 1) / 2;
}
return ans;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号