Day6 直线和圆 杂

直线和圆点一样多吗

参考：https://www.zhihu.com/question/46449164/answer/101450394

前几天看的强基书里面讲集合部分时，提到了“等势”的概念。也就是两个集合可以建立一一映射。

eg1：存在一个有无数房间的旅馆，每个房间都住满了人。现在来了两个人想入住。只需要让他们住 1、2 房，其他人往后面移 2 个即可。前后这两种方案就是等势的。

eg2：证明 \((0,1)\) 与 \([0,1]\) 等势。

考虑加入 \(0,1\)，不放构造映射：

\(x=0,y=1/2\)； \(x=1,y=1/4\)。

\(x=(\frac{1}{2})^n,y=(\frac{1}{2})^{n+2}\)。否则 \(y=x\)。\(\square\)

对于这个问题，构造如下：

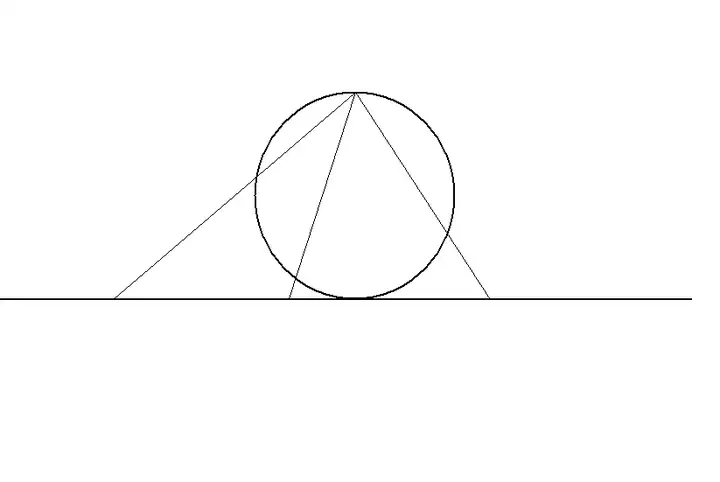
作圆的一条切线，过另一端的点随意作直线，则这条动直线可以过圆和直线的每一个点且一一对应。

小问题，圆最上面的点无法对应，这个像 eg2 一样处理即可。

曲线系方程

对于 \(C_i：F_i(x,y)=0\)，引入如下曲线系方程：

\(F_1(x,y)+\lambda F_2(x,y)=0\)

表示过 \(C_1,C_2\) 交点的曲线，除去 \(C_2\)。