线性表

目录

• 一、线性表：
• • 1.顺序表：
  • • • 实现：
      • ex-ky：
  • 2.链式表：
  • • • 实现：
      • ex-ky：

---

一、线性表：

1.顺序表：

1. 本质上就是数组，一种特殊的数组。
2. 结构包含：数组指针，表长，表容量。

实现：

//顺序表：
#include<iostream>
using namespace std;
#define MAXSIZE 20
typedef int ElemType;
typedef int Status;
typedef struct
{
	ElemType *elem;
	int length;
	int size;
}SqList;

//初始化：
Status InitList(SqList &L)
{
	L.elem = new ElemType[MAXSIZE];
	
	if (!L.elem)
		return -2;         //OVERFLOW  -2  申请失败,退出
	
	L.length = 0;         //无数据
	L.size = MAXSIZE;     //容量设为MAXSIZE
	return 1;             //初始化成功
}

//插入元素：
//先看插入的位置与时机
Status InsertElem(SqList &L, int i, ElemType e)      //i：1开始
{
	if (i<1 || i>L.length + 1)
		return -1;        //ERROR  -1   插入位置不正确
		
	if (L.length == MAXSIZE)
		return -2;        //OVERFLOW  -1   容量已满
		
	int k;
	
	if (i <= L.length)       //插入 从右往左
	{
		for (k = L.length - 1; k >= i - 1; k--)
			L.elem[k + 1] = L.elem[k];
	}
	L.elem[i - 1] = e;
	L.length++;
	return 1;
}

//删除元素：
Status DeleteElem(SqList &L, int i, ElemType *e)
{
	if (i<1 || i>L.length)
		return -1;        //-1  ERROR  删除位置有误
		
	if (L.length == 0)
		return -1;        //-1  ERROR  表为空
	
	int k;
	
	*e = L.elem[i - 1];     //保存删除数据
	if (i < L.length)        //删除 从左往右
	{
		for (k = i; k < L.length; k++)
			L.elem[k - 1] = L.elem[k];
	}
	L.length--;
	return 1;
}

//查找元素：
Status LocateElem(SqList L, ElemType e)
{
	int i = 1;
	ElemType *p = L.elem;
	while (i <= L.length && *p != e)  //注意顺序
	{
		i++;
		p++;
	}
	if (i <= L.length)                //用i来和length判断
		return i;
	else
		return -1;
}

//返回元素：
ElemType GetElem(SqList L, int i)
{
	if (i<1 || i>L.length)
		return -1;                   //-1  ERROR  注意L元素中如果有-1的话，选择其他数值表示ERROR

	return L.elem[i - 1];
}

ex-ky：

• 简化顺序表：

直接用数组和一个整型变量简化顺序表

	int SqList[MAXSIZE];
	int length; 

• 插入

int SqList[] 无需加&，已经是引用型数据类型

int insertElem(int SqList[],int &length,int p,int e){	//插入位置p，插入元素e
	//非法，失败返回0
	if(p<0 || p>length || length==MAXSIZE)
		return 0;	
	
	//合法，从后往前，相继后移，直到p为止
	for(int i=length-1; i>=p ; --i)
		SqList[i+1] = SqList[i];
	
	//插入，len++
	SqList[p] = e;
	++length;
	return 1;
}

• 删除

int deleteElem(int SqList[],int length,int p,int &e){
	//非法，失败返回0
	if(p<0 || p>length-1)
		return 0;
	
	//合法，e保存元素，从p往后，相继前移，到尾为止
	e = SqList[p];
	for(int i=p; i<length-1 ;i++)
		SqList[i] = SqList[i+1];
	length--;
	return 1;
}

• 顺序表平均插入次数：（有n+1种插入可能）

1.先列举几个位置需要移动的次数
2.总结规律
3.求平均值

• 顺序表平均删除次数：（有n种可能）

过程类似上述插入

2.链式表：

1. 本质上是无头链表。
2. 结构包含：存储数据，next指针。
3. 使用结构体指针表示链式表。

实现：

#include<iostream>
using namespace std;
#define MAXSIZE 20
typedef int ElemType;
typedef int Status;
typedef struct LNode
{
	ElemType data;
	struct LNode * next;
//	struct LNode * prior;  //前驱节点
}LNode, *LinkList;
//初始化：
Status InitList(LinkList &L)
{
	L = new LNode;
	L->next = NULL;
	return 1;
}

//头插法创建链表：
void CreateListHead(LinkList &L, int n)//头插法
{
	L = new LNode;             //head node
	L->next = NULL;
	for (int i = 0; i < n; i++)
	{
		LinkList p = new LNode;
		cin >> p->data;          //输入数据
		p->next = L->next;
		L->next = p;
	}
}

//尾插法：
void CreateListTail(LinkList &L, int n)
{
	L = new LNode;             //head node
	L->next = NULL;
	LinkList R = L;			   //tail node
	for (int i = 0; i < n; i++)
	{
		LinkList p = new LNode;
		cin >> p->data;          //输入数据
		p->next = R->next;
		R->next = p;
		R = p;
	}
}

//插入元素：
Status InsertElem(LinkList &L, int i, ElemType e)  //i:1--end+1
{
	LinkList p, q;
	p = L;
	int j = 1;
	while (p && j < i) //j到i前一个元素停止
	{
		p = p->next;
		j++;
	}
	if (!p || j > i)
		return -1;
	q = new LNode;      //q存待插入元素
	q->data = e;
	q->next = p->next;  //后接q
	p->next = q;        //前接q
	return 1;
}
//删除元素：
Status DeleteElem(LinkList &L, int i, ElemType *e)
{
	LinkList p, q;
	p = L;
	int j = 1;
	while (p->next && j < i)  //p->next:优化；i次序不存在不会ERROR
	{
		p = p->next;
		j++;
	}
	if (!(p->next) || j > i)
		return -1;
	q = p->next;
	p->next = q->next; //前连后，绕过q
	*e = q->data;      //指针e存储删除数据
	delete(q);
	q = NULL;
	return 1;
}
//查找元素：
Status GetElem(LinkList L, int i, ElemType *e)
{
	if (i < 1)
		return -1;   //-1 ERROR  
	int j = 1;
	LinkList p;
	p = L->next;     //D1 node
	while (p && j < i)  //只有p为空&&j=i时，退出
	{
		p = p->next;
		j++;
	}
	if (!p)
		return -1;  //j
	*e = p->data;   //传入进来的e指针存储目标元素值
	return 1;
}
//清空表：
Status ClearList(LinkList &L)
{
	LinkList p, q;
	p = L->next;  //D1 node
	while (p)
	{
		q = p->next; //q = next node
		free(p);
		p = q;
	}
	L->next = NULL;
	return 1;
}

ex-ky：

• ***静态链表：***

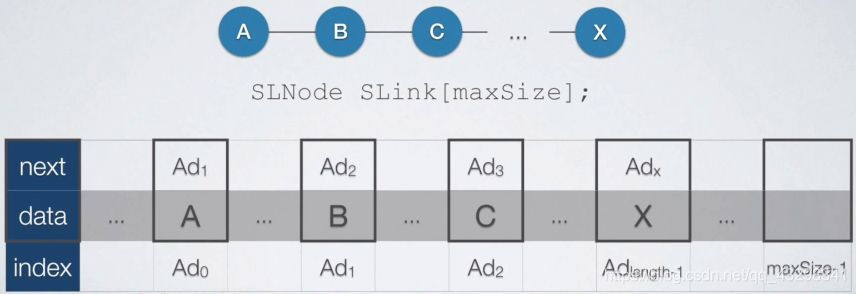
//定义:
typedef struct{
	int data;	
	int next;	//类似next指针，现在不指向节点，而是数组节点的下标。
}SLnode;

SLnode SLink[MAXSIZE];

int p = Ad0;	//类似头指针

SLink[p].data;	//类似于p->data
SLink[p].next;	//类似于p->next