莫队算法
莫队是由原国家队队长莫涛提出的算法,当时只分析了普通莫队算法,现在有带修莫队,莫队二次离线,回滚莫队,树上莫队等多种变式,本文将在此做一些介绍。
普通莫队算法
接下来以 [SDOI2009] HH的项链 为例题来阐述。
题意就是多次询问区间种类数,经典做法有在线的可持久化线段树,离线的树状数组和莫队,其中树状数组跑最快,洛谷也只放了树状数组过,想交其他算法可以上 LOJ。
区间种类数问题。
首先暴力肯定就是开一个 \(cnt\) 数组记录每个数出现的次数,每次一个一个加入,例如加入下标为 \(x\) 的数,其中 \(now\) 代表答案:
void add(int x){if(++cnt[a[x]]==1)now++;}
但是这样是 \(O(nq)\) 的。但是做了的事没有白做,我们可以从上一个区间的答案转移到下一个区间,即 \([l,r]\) 可以扩展到 \([l-1,r],[l+1,r],[l,r+1],[l,r-1]\),这时候就涉及删除下标为 \(x\) 的数:
void del(int x){if(--cnt[a[x]]==0)now--;}
但如果一直重复询问 \([1,1],[1,n]\),依然退化成 \(O(nq)\)。这时候就得想办法减少指针移动,抽象到二维坐标系,就是给定 \(m\) 个点,求其的曼哈顿距离最小生成树,很可惜这是个 NP 完全问题,是无法在多项式时间内解决的,不过我们不必最优,能比朴素算法快即可。离线后排序,排序方法为:先分块,按 \(l\) 所在的块为第一关键字,\(r\) 的大小为第二关键字排序。这样按照前文的算法去跑,时间复杂度就变成了 \(O(n\sqrt{n})\)。简单证明一下,在左端点同一块中,右端点最多移动 \(n\) 次,共 \(\sqrt{n}\) 个块,故右端点移动是 \(O(n\sqrt{n})\) 的。左端点一次询问最多移动 \(\sqrt{n}\) 次,故左端点移动 \(O(m\sqrt{n})\)。再加上排序 \(O(n\log n)\),所以总复杂度:
视 \(n,m\) 同阶,故最终时间复杂度为 \(O(n\sqrt{n})\)。
当然,当 \(n,m\) 不同阶时,块长取 \(\sqrt{n}\) 并不最优,要列均值不等式去算,但是 \(\sqrt{n}\) 的块长足以通过绝大多数题目。
例题代码:
const int N=1e6+7;
int n,m,ans[N],a[N],now,cnt[N];
struct bb{
int l,r,id,bel;
}q[N];
bool cmp(bb a,bb b){
return a.bel==b.bel?a.r<b.r:a.bel<b.bel;
}
void add(int x){if(++cnt[a[x]]==1)now++;}
void del(int x){if(--cnt[a[x]]==0)now--;}
int main(){
read(n);
int len=sqrt(n);
for(int i=1;i<=n;i++)read(a[i]);
read(m);
for(int i=1;i<=m;i++)
read(q[i].l),read(q[i].r),q[i].bel=(q[i].l-1)/len+1,q[i].id=i;
sort(q+1,q+m+1,cmp);
int l=1,r=0;
for(int i=1;i<=m;i++){
while(l>q[i].l)add(--l);
while(r<q[i].r)add(++r);
while(l<q[i].l)del(l++);
while(r>q[i].r)del(r--);
ans[q[i].id]=now;
}
for(int i=1;i<=m;i++)printf("%d\n",ans[i]);
return 0;
}
注意上面的四个 while,位置不能乱,得先扩张后收缩,不然可能 \(r<l\),如果处理某些与 \(l,r\) 有关的问题时就会挂。但是例题是没有影响的,咋写都行,不过还是按要求写避免出锅。
奇偶化排序
当我们处理完一个块的答案后,当前的 \([l,r]\) 区间可能非常大,而下一个块第一个询问的 \([ql,qr]\) 又十分小,指针移动量就很大。于是我们可以先处理下一个块的大区间减少移动,再处理小区间;再下一个块就先处理小区间,再处理大区间。
得出新的排序方法:还是按 \(l\) 所属的块为第一关键字,如果这个块的编号是奇数,按 \(r\) 从小到大排;如果这个块的编号是偶数,按 \(r\) 从大到小排。
奇偶化排序可以提高约 \(30\%\) 的效率,在一些需要卡常的题中常用。
struct bb{
int l,r,bel,id;
bool operator<(const bb t)const{
return bel!=t.bel?bel<t.bel:((bel&1)?r<t.r:r>t.r);
}
}q[N];
带修莫队
带修莫队相比普通莫队需要加一个时间戳,即需要移动三个指针 \([l,r,time]\),排序方法变成以 \(l\) 所在块为第一关键字,\(r\) 所在块为第二关键字,\(t\) 的大小为第三关键字。分块大小也需要改变, \(B=n^{\frac 2 3}\),时间复杂度 \(O(n^{\frac 53})\),不会证明,大神博客可以看看。
询问的结构体需要多保留前一个修改的时间戳。如果访问到一个修改被当前区间包含,则将其修改,但是如果我们后面又倒退回来,应该将其改回来,即需要支持回溯操作,看似很难,其实只需要每次修改时 swap 修改的值与原值即可,比如现在要把 \(4\) 改为 \(3\),改完后交换一下,下一次倒退回来就是 \(3\) 改为 \(4\) 了。
模板题代码:
const int N=1e6+7;
int n,m,qcnt,ccnt,len,a[N],ans[N],cnt[N],now;
int getbl(int x){return (x-1)/len+1;}
struct bb{
int l,r,id,pre;
bool operator<(const bb t)const{
return getbl(l)!=getbl(t.l)?l<t.l:(getbl(r)==getbl(t.r)?pre<t.pre:r<t.r);
}
}q[N];
struct cc{
int pos,val;
}c[N];
void add(int x){if(++cnt[a[x]]==1)now++;}
void del(int x){if(--cnt[a[x]]==0)now--;}
void work(int tim,int i)
{
if(q[i].l<=c[tim].pos&&c[tim].pos<=q[i].r){//被包含才操作
if(--cnt[a[c[tim].pos]]==0)now--;
if(++cnt[c[tim].val]==1)now++;
}
swap(c[tim].val,a[c[tim].pos]);//交换,使其支持回溯
}
int main(){
read(n);read(m);
for(int i=1;i<=n;i++)read(a[i]);
len=pow(n,0.6666666);
char op[5];
for(int i=1;i<=m;i++){
scanf("%s",op);
if(op[0]=='Q'){
read(q[++qcnt].l);read(q[qcnt].r);
q[qcnt].pre=ccnt;q[qcnt].id=qcnt;
}
else read(c[++ccnt].pos),read(c[ccnt].val);
}
sort(q+1,q+qcnt+1);
int l=1,r=0,tim=0;
for(int i=1;i<=qcnt;i++){
while(l<q[i].l)del(l++);
while(l>q[i].l)add(--l);
while(r<q[i].r)add(++r);
while(r>q[i].r)del(r--);
while(tim<q[i].pre)work(++tim,i);//时间戳少了
while(tim>q[i].pre)work(tim--,i);//时间戳多了
ans[q[i].id]=now;
}
for(int i=1;i<=qcnt;i++)printf("%d\n",ans[i]);
return 0;
}
树上莫队
参考了 洛谷@eee_hoho 的文章。
注意莫队是开指针在序列中操作,于是我们想办法将树拍平成序列,引入一个叫欧拉序的玩意:从根节点 dfs,每个点入栈出栈的顺序,记为 \(st_i\) 和 \(ed_i\),如下面这颗树:
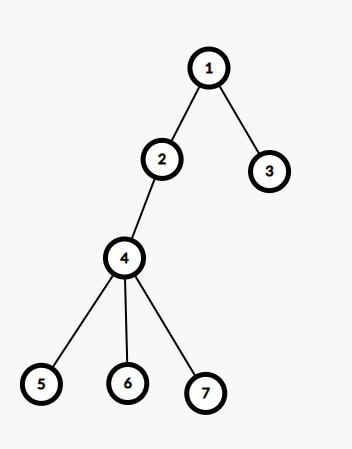
其欧拉序为 \((1,2,4,6,6,5,5,7,7,4,2,3,3)\)。和树剖的 dfs 序很像,但是出栈也得打标记。
有什么用呢,比如我们选两个点 \(u,v\):
-
如果 \(u\) 是 \(v\) 的祖先,如 \((2,5)\) 这对点,调用 \([st_2,st_5]\) 这段区间为 \((2,4,6,6,5)\),注意到 \(6\) 出现了两次,即进去又出来了,不属于 \(2\) 到 \(5\) 的路径,于是只统计出现一次的 \((2,4,5)\)。
-
如果 \(u\) 不是 \(v\) 的祖先,如 \((5,3)\) 这对点,则调用 \([ed_5,st_3]\) 这段区间为 \((5,7,7,4,2,3)\) (得保证 \(st_u<st_v\)),同理只管出现一次的 \((5,2,4,3)\)。但是发现 lca 没了,需要算上 lca。
又要算欧拉序又要算 lca,推荐直接树剖,常数小避免莫队卡常。
关于如何处理重复出现,只需维护 \(use_i\) 表示 \(i\) 有没有加过,如果 \(use_i=0\) 则加入该点,否则删掉该点。
模板题代码:
const int N=2e5+7;
using namespace std;
struct bb
{
int l,r,id,lca,bel;
bool operator<(const bb t)const{
return bel!=t.bel?bel<t.bel:((bel&1)?r<t.r:r>t.r);
}
}q[N];
int n,m,a[N],cnt[N],now,use[N],ans[N],b[N];
int st[N],ed[N],f[N],idx,sz[N],g[N],dep[N],big[N],top[N];
vector<int>edge[N];
void dfs1(int u,int fa){
f[u]=fa;sz[u]=1;dep[u]=dep[fa]+1;
for(int v:edge[u])if(v!=fa){
dfs1(v,u);
sz[u]+=sz[v];
if(sz[v]>sz[big[u]])big[u]=v;
}
}
void dfs2(int u,int tp){
top[u]=tp;st[u]=++idx;g[idx]=u;
if(big[u])dfs2(big[u],tp);
for(int v:edge[u])if(v!=big[u]&&v!=f[u])dfs2(v,v);
ed[u]=++idx;g[idx]=u;
}
int lca(int x,int y){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
x=f[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
return x;
}
void add(int x){now+=(++cnt[a[x]]==1);}
void del(int x){now-=(--cnt[a[x]]==0);}
void calc(int x){(!use[x])?add(x):del(x);use[x]^=1;}
int main(){
read(n);read(m);
for(int i=1;i<=n;i++)
read(a[i]),b[i]=a[i];
sort(b+1,b+n+1);
int nn=unique(b+1,b+n+1)-b-1;
for(int i=1;i<=n;i++)a[i]=lower_bound(b+1,b+nn+1,a[i])-b;
for(int i=1,x,y;i<n;i++){
read(x);read(y);
edge[x].pb(y);edge[y].pb(x);
}
dfs1(1,0);dfs2(1,1);
int len=n*2/sqrt(m*2/3);
for(int i=1,x,y;i<=m;i++){
read(x);read(y);
if(st[x]>st[y])swap(x,y);
q[i].id=i;q[i].lca=lca(x,y);
if(q[i].lca==x){
q[i].l=st[x];q[i].r=st[y];
q[i].bel=(q[i].l-1)/len+1;
q[i].lca=0;
}
else{
q[i].l=ed[x];q[i].r=st[y];
q[i].bel=(q[i].l-1)/len+1;
}
}
sort(q+1,q+m+1);
int l=1,r=0;
for(int i=1;i<=m;i++){
while(l>q[i].l)calc(g[--l]);
while(r<q[i].r)calc(g[++r]);
while(l<q[i].l)calc(g[l++]);
while(r>q[i].r)calc(g[r--]);
if(q[i].lca)calc(q[i].lca);
ans[q[i].id]=now;
if(q[i].lca)calc(q[i].lca);//lca要删掉,避免影响后面操作
}
for(int i=1;i<=m;i++)
printf("%d\n",ans[i]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号