【12 月小记】Part 1: KMP / Trie 树

KMP / Trie 树

一、Trie 树

1. 用处

Trie 树可以充分利用多个字符串的公共前缀，通过空间换时间，大幅降低查询操作的时间开销。

事实上，Trie 树还有其变种 0-1 Trie，也是一种好用的数据结构，常用于解决异或最优解问题。

因为我们将一堆字符串拍到了一个树上，所以这个树可以看作一个由字符串构成的某种形式的集合。因此，在使用某模式串匹配这些字符串时，Trie 树就是一种很好的选择——因为只需要在这个树上查询，而不需要分别遍历每个字符串进行查询。

由上，我们可以总结出最核心的一句话：Trie 树常用于解决“一对多”类型的问题。

2. 构建原理

我们来看一张示意图，在网上搜到的，感觉很有代表性。

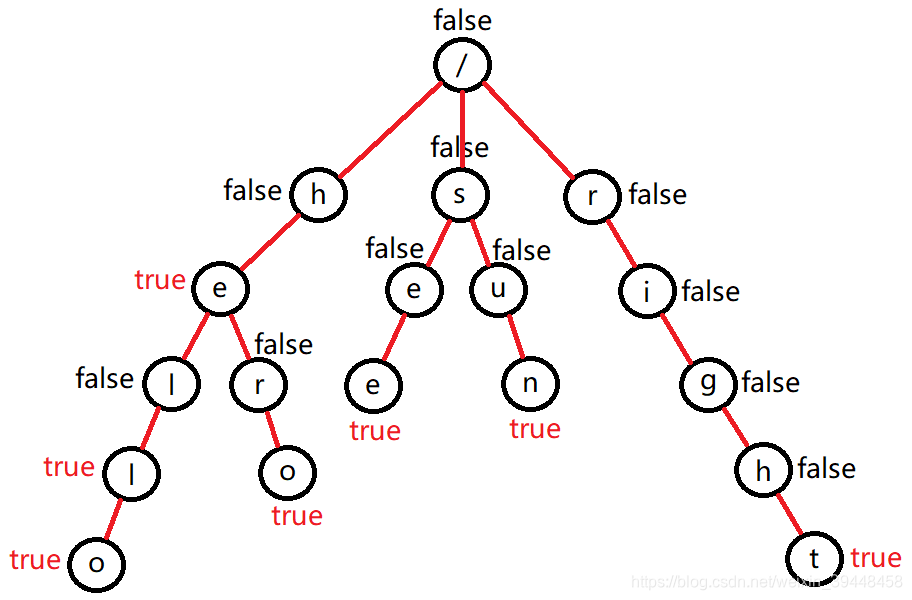
目前你有以下单词：he, hello, hero, see, sun, right，想要把这些单词放到 Trie 树上，可以采用如下方法构建 Trie 树。

• 根节点不包含字符，除根节点外每一个节点都只包含一个字符；
• 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串；
• 每个节点的所有子节点包含的字符都不相同；
• 任意单词最后一位的字符需要被打上标记（图中的 true 或 false）。

3. 代码实现

我个人比较喜欢结构体封装的写法。

(1) 树的节点

Trie 树上的每个节点一般都有以下属性：

• 某一编号孩子是否存在；
• 末尾标记；
• 被加入了几次（计数器）。

所以我们可以写出：

struct Node {
    int son[26];
    bool end;
    Node() { end = 0; memset(son, 0, sizeof(son)); }
} t[N << 5];

(2) 编码

我们需要对每个字母进行编码。假设这里所有的字符都是小写字母，那么我们可以将每个字符减去字符 'a' 获取到这个字符的编码，范围是 0 ~ 25。

int encode(char c) { return c - 'a'; }

(3) 插入

我们需要从头开始遍历这个单词。维护一个指针 cur，表示目前的节点编号。

不断地寻找 cur 节点的子节点，使得这个子节点代表这个单词的目前那位字符。如果这个子节点不存在，则创建这个节点，并赋予其编号。因此，我们需要维护一个编号计数器 tot，初始值为 0，在创建节点的过程中不断自增。

过程中，不断累加字符节点访问的次数。最后，给最后一位字符打上末尾标记。

void insert(string str) {
    int cur = 0;
    for (auto c : str) {
        int code = encode(c);
        if (!t[cur].son[code]) t[cur].son[code] = ++tot;
        cur = t[cur].son[code];
        t[cur].cnt++;
    }
    t[cur].end = 1;
}

(4) 查询

不同的 Trie 树问题中，查询单词的操作方法不同，甚至有的题目不需要查询操作，但其本质都是在树上进行遍历。故这里不给出代码。

4. 例题

(1) P1481 魔族密码

这题一定能用暴力糊过去，但是我们为了学 Trie 树，先这么写吧。

我们维护一个 Trie 树，把所有单词拍进去。

写一个查询函数，返回目前这个单词的路径上存在多少个末尾标记（包括自身）。对于每个单词的查询函数返回值，其最大值即为答案。

(2) P2580 于是他错误的点名开始了

仍然，map 能做，但是仍用 Trie 树。

维护一个 Trie 树，把所有单词拍进去。

查询过程中，如果这个单词存在，则输出 OK 并把末尾节点的权 + 1。如果这个单词不存在，输出 WRONG。否则，输出 REPEAT。

其实这个题就是一对多的问题：对于每个要询问的字符串，查询它关于每个点名册上的名字的答案。

(3) P8306 【模板】字典树

查询函数返回的是末尾节点的 cnt。其余实现基本相同。

(4) P2536 [AHOI2005] 病毒检测

这道题我为了练 Trie 树，所以解法是搜索，当然还有更好的 dp 解法，以后再研究。

我们再复习一下 Trie 树里面存的是啥。Trie 树的节点结构体里面，通常要存三个量。

1. cnt，表示这个节点被记录了几次（但在这道题里用不上）。

2. son[M]，表示它的儿子的编号。这里 M 是字符集大小。

3. end，表示这个节点是否是单词的终点。

这里引用一句非常精辟的话，“一对多”的字符串匹配通常要用“多”的字符串建 Trie 树。

所以，我们把所有 DNA 片段弄到 Trie 树上，然后用模式串在 Trie 树上跑 BFS。

因为模式串的字符类型有三种，所以这里需要分类讨论。

1. A/C/T/G：判断一下目前模式串指向的是不是树上指向的字符，往下搜即可。

2. *：这是这道题的难点。可以将其分为两种子情形。

1)不匹配任何字符。

2. 匹配字符，等价于不用将指向模式串的指针右移一位的 ? 字符；换言之，等价于 ? 和一个 * 连起来。

3. ?：不管模式串目前指向的是什么，直接往下搜。

注意，这里 BFS 的队列得传两个参数，一个是目前在 Trie 树上的节点编号，另一个是目前指向模式串的位置。

为了避免重复搜到一个结果，这里为每个 Trie 树上的节点打一个标记，表明这个节点是否被记到贡献里。否则你只会得到 60 pts。

记住，Trie 树的第一个节点编号为 0。

---

以下是一些 0-1 Trie 的练习题。

(5) P10471 最大异或对 The XOR Largest Pair

同下一题。

(6) P4551 最长异或路径

这道题需要一些性质。

1. 在一棵树上，节点 u 到 v 的异或路径，恰等于节点 u 到根节点的路径异或和与节点 v 到根节点的路径异或和的异或值。因为 lca(u, v) 这个节点到根节点的路径被异或了两次，相当于没异或。
2. 进一步地，如果把所有节点到根节点的路径异或和预处理出来，问题就变为了：一个数组里选俩数，让它们的异或值最大（这不就是 P10471 吗）。这里我们想到使用 0-1 Trie 这种数据结构。
   • 先把所有的数组内元素拍到 Trie 上。
   • 然后对于一个数组内的元素 val，我们考虑在 Trie 树上寻找能和 val 产生最大异或和的值。对于 val 的每一位，尽量选择与这一位相异的二进制位；如果 Trie 树上没有与其相异的二进制位，再选择与其相同的二进制位。
   • 把你选择的所有二进制位拼起来，就是能与 val 产生最大异或和的值。因为我们是在树上操作的，所以这一过程的时间复杂度是 \(O(\log n)\) 的。
   • 对于所有的 pre[i]，进行上面的过程，总的时间复杂度是 \(O(n \log n)\) 的。

(7) P6824 「EZEC-4」可乐

这是一道 Trie 树的好题，让我对异或有了更深的理解。

这题的样例没有任何代表性，所以我们先打一个 29 pts 的暴力，造几组样例。（策略！）

首先，我们再次引用那句话，“一对多的问题常用 Trie 树解决”，所以这里我们把所有的 a 数组值拍到一个 0-1 Trie 上，在这棵树上跑出来。

这里要比较的两个值是 a ⊕ x 和 k，要求是 a ⊕ x <= k。

我们考虑，因为答案 x 的最大值就是两倍 a 的最大值（显然凑不出来更大的数了），所以可以枚举答案 x，在 Trie 树上带着这个 x 跑，看看能跑出来多少贡献。

我们要使得 a ⊕ x <= k。这里考虑逐个二进制位比较 a ⊕ x 和 k。可以考虑分类讨论。以下记 k 的当前二进制位为 bit_k，x 的则为 bit_x。

1. 当 bit_k = 1 时：

   1. 如果 a ⊕ bit_x = 0，那么说明当前 a ⊕ x 的这一个二进制位已经是 0 了，而这时 k 所对应的位则是 1；进而说明，无论 a ⊕ x 后面的二进制位怎么变化，它都不可能再比 k 大了。因为 a ⊕ bit_x = 0 等价于 a = bit_x，所以这里直接把 bit_x 这个子节点的计数值加到贡献里。

   2. 如果 a ⊕ bit_x = 1，即 a = bit_x ⊕ 1，就说明还有条件成立的希望，但是目前比不出来，继续往下搜 bit_x ⊕ 1 这一子节点。

2. 当 bit_k = 0 时：

   1. a ⊕ bit_x = 1 显然不合法。

   2. a ⊕ bit_x = 0 同上，继续往下搜。

最后枚举 x，统计最大的答案即可。

(8) CF1285D Dr. Evil Underscores

在 Trie 树上进行 DFS 搜索的案例。

这仍然是一个“一对多”的问题，所以把所有的 a 数组值拍到 0-1 Trie 上。

为了使得 max(a ⊕ x) 尽可能小，我们从 Trie 树的根开始遍历。考虑以下情况：

1. 目前访问的节点有两个子节点：

   这会使得：无论 x 取何值，总会存在一个 a，使得 a 的这一位与 x 的这一位不相同，即 max(a ⊕ x) 的这一位总会是 1。这就说明，我们需要将这一位 1 的值纳入贡献，然后接着搜其左右节点的最小答案。

2. 目前访问的节点只有一个子节点：

   这说明，我们得构造出来一个 x，使得 x 的这一位与这个子节点相同，即异或出来的结果等于 0，进而使得答案尽可能小。所以，这里不将任何值纳入贡献，直接搜索这个子节点即可。

3. 如果目前的位数小于 0，直接返回。

(9) CF665E Beautiful Subarrays

题意：统计序列 a 的子序列 [l, r] 中，使得其按位异或和大于或等于 k 的序列总数。

首先我们需要明确一个知识点：异或前缀和。我们知道，一个数被异或偶数次后等效于没异或。所以可以维护异或前缀和数组 s[i] 表示区间 [0, i] 的异或和。若要查明区间 [l, r] 的异或和，可以使用 s[r] ⊕ s[l - 1] 来查询，单次访问是 \(O(1)\) 的。

对于这种“一对多”的“异或最优解”问题，一般使用 Trie 树解决。

我们把所有的 s 拍到 Trie 树上，然后去定义一个函数，统计 Trie 树上，一共有多少个树，使其结果与 x 的异或值大于或等于 k。

这里和 [P6824 可乐] 那道题的思路就基本一样了，分类讨论。

• 当 k = 1 时，必须要让 x ⊕ s = 1，即走向 x ⊕ 1 那个子节点，才能使目前树上的这一位为 1，才有希望使得异或值大于或等于 k；

• 当 k = 0 时：

  • 如果 x ⊕ s = 1，说明不管如何，s 都会比 x 大了，直接把目前节点的计数器往贡献里加即可；
  • 如果 x ⊕ s = 0，则继续搜索 x 这个子节点，才能使得 x ⊕ s = 0。

最后遍历每个 s，在 Trie 树里统计，累加贡献即可。时间复杂度应为 O(ωn)。

值得注意的是，在计算的过程中，必须避免出现区间左右端点反过来的情形，即形如 s[l] ⊕ s[r - 1] 的情形（否则会算重，同时也不符合异或前缀和的意义），所以我们需要一边累加贡献，一边往 Trie 树里扔数组值。

这空间卡的，无敌了哥们。似乎还得用高精？

二、KMP

1. 史话

KMP 算法是由高德纳（Donald Knuth）、沃恩·普拉特（Vaughn Pratt）和詹姆斯·H·莫里斯（James H. Morris）于 1974 年共同构思的，并在 1977 年联合发表。

2. 用处

KMP 算法可以用于高效的字符串匹配，或者字符串前后缀问题。

其核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。

该算法的时间复杂度是线性的。

3. 如何工作

模板例题：P3375 【模板】KMP

(1) next 数组

a. 定义

ne[i] 表示模式串 t[1...i] 中，最长的相等前后缀的长度（不包括自身）。

b. 计算 next 数组

for (int i = 2, j = 0; i <= m; i++) {
    while (t[i] != t[j + 1] && j > 0) j = ne[j];
    if (t[i] == t[j + 1]) j++;
    ne[i] = j;
}

解释：

• i 遍历模式串的每个位置（从 2 开始，因为长度为 1 时前后缀为空）

• j 记录当前位置之前的匹配前缀长度

关键逻辑：

• 当 t[i] 与 t[j+1] 不匹配时，利用已有的 ne[j] 回退到更短的前缀位置
• 匹配成功时，j 增加
• 将当前的 j 值赋给 ne[i]

示例： 模式串 "ABABC"

• ne[1] = 0 （"A" 无公共前后缀）
• ne[2] = 0 （"AB"，前缀"A"，后缀"B"，不相等）
• ne[3] = 1 （"ABA"，前缀"A" = 后缀"A"）
• ne[4] = 2 （"ABAB"，前缀"AB" = 后缀"AB"）
• ne[5] = 0 （"ABABC"，无公共前后缀）

(2) 匹配

for (int i = 1, j = 0; i <= n; i++) {
    while (s[i] != t[j + 1] && j > 0) j = ne[j];
    if (s[i] == t[j + 1]) j++;
    if (j == m) {
        cout << i - m + 1 << '\n';
        j = ne[j];
    }
}

流程：

1. i 遍历主串 s 的每个字符（从 1 开始）
2. j 记录当前模式串已匹配的长度
3. 关键优化：当 s[i] 与 t[j+1] 不匹配时，不回溯 i，而是将 j 移动到 ne[j]
   • 因为 ne[j] 保证了 t[1...ne[j]] 与 s[i-ne[j]...i-1] 已匹配
4. 当完全匹配时 (j == m)，输出起始位置，并利用 ne[j] 继续寻找下一个可能的匹配

(3) 关键思想总结

1. 利用已知信息：通过分析模式串自身结构，预先计算最长公共前后缀
2. 避免无效比较：匹配失败时不移动主串指针，而是调整模式串指针
3. 空间换时间：使用 next 数组存储模式串的"自相似性"信息

4. 例题

(1) P4391 [BalticOI 2009] Radio Transmission 无线传输

性质：字符串 s（长度为 n）的最短周期等于 n - ne[n]。例如：

{cab}[cab][ca]
     [cab][ca]{bca}

把原字符串按照它的最长 next 匹配上，可以逐段证明上下两段相等，进而空出来的部分就是最短周期.

(2) P3435 [POI 2006] OKR-Periods of Words

从 P4391 可以知道，一个长度为 len 的字符串 s 的最短周期，恰好等于 s.len - ne[s.len]。

进一步，对于字符串 s 的 border（记为字符串 t），它的最短周期是 t.len - ne[t.len]。

所以，对于 s 的最后一位，不断递归地寻求它的 next，最后找到的 border 长度，就是最小的那个 next 数组值，进而 n - next 就是最大的周期长度。

通俗一点说，就是用 next 数组不断往前跳，直到跳到 0 为止，来找到原串的最短 border。

因为我们求的是原串的所有前缀的答案和，所以可以记忆化一下，不用每次都一步一步跳了。

KMP 中，在 next 数组上“跳”的思想非常有用，值得记住。

(3) P2375 [NOI2014] 动物园

神题，KMP 思想集大成者。

首先，我们考虑无视限制的做法：使用 num[i] 表示子串 [1, i] 内存在的可重叠的相同前后缀长度（包括它本身。至于为什么呢，后面再说）。

我们先要跑出来这个串的 next 数组。因为一个串的 next 肯定会对这个串的 num 产生 1 的贡献，所以可以发现递推式：num[i] = num[ne[i]] + 1。

然后可以考虑一个 50 pts 的做法。我们知道，某些 KMP 题目中存在一种基本套路，它是指，对于每个 i，令指针 j = i，不断递归地让 j = ne[j]，这样就可以找到 i 的所有前后缀（也就是前文说的“跳”的思想）。

那么考虑，在递归过程中，当指针 j <= i / 2 时，表示目前 j 指向的这个前后缀是不会和 i 产生重叠的，而且 ne[j] 以及 ne[ne[j]] 等进一步递归的前后缀都不会和 i 产生重叠，所以这里直接将目前的这个 num[j] 扔到贡献里。

但这样有一个问题。对于每一个 i，都会跳很多次；甚至在一个全是 a 的字符串中，它会跳 n² 次。这样的话，时间复杂度会变成 O(n ^ 2) 的。

这里我们又想到 KMP 算法的思想。我们知道，在跑 next 数组的时候，指针 j 永远指向的是 ne[i]。所以我们再套一个 KMP 板子，利用这个指针 j，当 j 超限时，给它往回跳。因为指针 j 在原字符串上从左往右走，虽然 j 还得往回跳，但总之 j 跳的总步数就是字串长度 n，足以通过。

最后解释一下为什么前面算 num 的时候要把整个子串本身也算作一个相等前后缀。因为算答案的时候，我们要先找到不重叠的最大子串，然后用它的相等前后缀个数来推答案，如果直接在 num 里面包括整个子串本身，后面用起来比较方便，因为在用 num[j] 的时候本身就已经把 j 当作子串了。