浅谈二分的边界问题
转自:洛谷日报https://www.luogu.org/blog/tarjanfloydDP/qian-tan-er-fen-di-bian-jie-wen-ti
作者:曦行夜落
Part1:二分的中心思想
这是一个杯具,当你将二分的l+1<r写成l<r时,相信很多人都讨厌二分的边界,每次都弄不清楚二分的l和r要等于mid,还是mid-1,又或者是mid+1,这导致了很多人因此失分,那么,到底要怎么做才能区分二分的边界呢?
二分的思想主要分三种:
- l和r代表的“成本值”均可行,且有一个ans变量记录当前的最优
- l和r代表的“成本值”均可行,最后的答案是l或r
- l代表的“成本值”可行,r不可行,最后的答案是l
下面我们将依次讲解1、2两种,第三种不推荐使用,比较容易出错
注:下面的全部模板都是求最小的满足指定条件的数(例如洛谷P2370)
Part2:写法一——记录答案法
话不多说,先上模板:
while (l<=r) { int mid=(l+r)/2; if (check(mid)) { ans=mid; r=mid-1; } else l=mid+1; } printf("%d",ans);
首先,限制条件为l小于等于r,也就意味着结束需要l>r
第一步显然就是找区间中点
check(mid)是一个bool函数,返回mid是否可行,下面就是分情况讨论
1、id可行,此时记录ans=mid,也就是mid是目前最优解,然后缩小查找范围:r=mid-1,寻找有没有更小的解
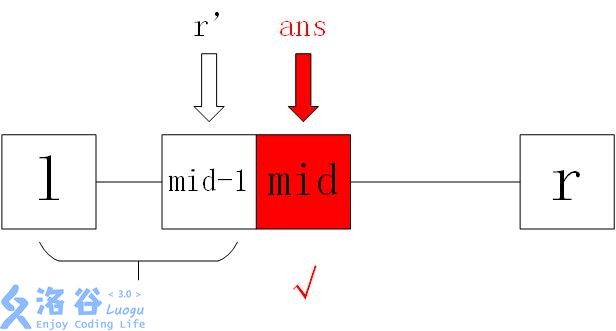
2、mid不可行,此时令l=mid+1,找更大的解来满足条件
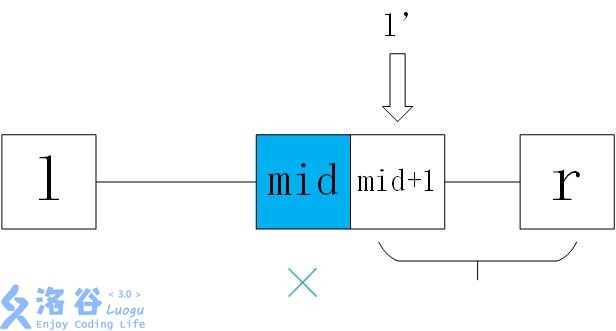
1、也就是说,当mid可行,就记录mid,然后找有没有更优的,否则就退而求其次,牺牲数据的优秀度来满足条件
例如:要找出能够当飞行员的成绩最差的候选人,测试成绩居中的人,看他能不能胜任。
2、可以,记下他,然后对比他弱的人进行测试(ans=mid r=mid-1)
3、不行,对比他强的人进行上述操作(l=mid+1)
Part3:写法二——不记录法
先上模板:
while (l<r) { int mid=(l+r)/2; if (check(mid)) r=mid else l=mid+1; } printf("%d",l); //r也可以
这里,当l==r时循环停止,此时无论输出l还是输出r都可以。取中点不讲。这里我们要保证l和r都是暂时可行的(没有证明不可行)的,所以当mid被判定为可行时,r应该取到mid而不是mid-1,因为这里没有ans来记录,如果r取了mid-1,我们就永远丢失了mid这个可行解(mid永远取不到了),从而导致答案错误。
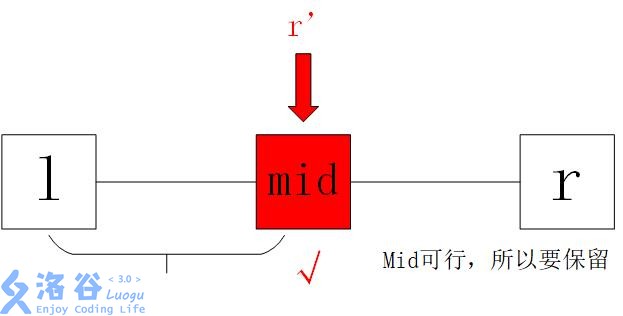
如果mid不可行,仍然取l=mid+1,因为mid是不可行的,而我们要保证l可行
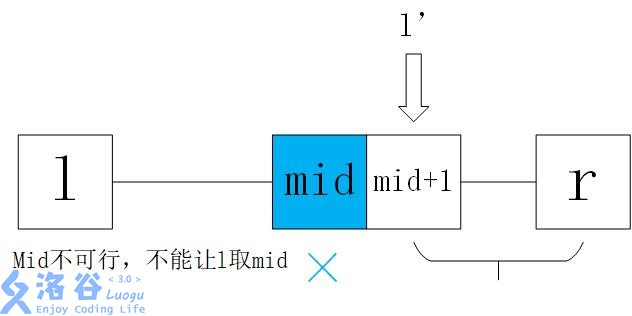
这里就是说,当mid可行,就在l~mid区间里面找(往小了找),否则就在mid+1~r来找,始终要保证l、r均可行且尽量靠近
这里的重点:l和r都要暂时可行且l要极小,r要极大
前方高能,划重点:
**打个比方:一群选手按实力顺序排好,然后我们要找出能够AK IOI的实力最差的选手,那么我们选实力居中的那个,测试他能不能AK IOI:
- 可以(check(mid)=true)。那么实力比他更强的选手可以回去了,因为他们一定能AK IOI,而且实力比刚刚测试的那位要高。但是那个测试过的就可以“暂时安全”,因为他是目前最优解(能AK且实力最差),这一个操作就是r=mid
- 不能(check(mid)=false)。那么他以及实力比他弱的全部淘汰,这个操作是l=mid+1
然后用新的区间不断重复即可
注:此处满足单调性,就是说如果X能AK IOI,那么比他强的也一定能,否则比他弱的一定不能**
再举个例子:
要找不能AK IOI的最强选手(注意,题设相反),那么照样按实力排好,测试居中的那个:
- 可以(check(mid)=false)。此时他以及比他更强的都不能符合要求(我们要找不能AK的,不是AKer),所以r=mid-1
- 不能(check(mid)=true)。此时比他弱的人全部淘汰(比他弱的更不能,而且实力比他弱),这个操作是l=mid
之后就是对新的区间进行一样的操作
但是这个例子要注意一个特殊情况,如果l=2,r=3,mid=5/2=2,此时测试的check(mid)如果为true,那么l和r将永远卡在2和3,所以在此处,我们取的中点要靠右,也就是(l+r+1)/2,这样就能保证l和r不死循环
通过上述几个例子,应该能够比较直观的认识到这个不记录式的用法。
Part4:二分查找
二分查找是利用二分的思想,在一个有序递增数列中查找某个值的算法。
例子:猜数游戏,老少咸宜,在1~100中想一个数key,然后让别人猜,每猜一次,就会告诉别人是大了还是小了。这个很经典了,先猜中间那个,然后如果大了就猜更小的,否则猜更大的,如果直接猜中就结束——与二分思想不谋而合
1、查找值为key的元素下标,不存在返回-1
首先我们看看模板
int l=1,r=n; while (l<=r) { int mid=(l+r)/2; if (a[mid]==key) return mid; else if (a[mid]>key) r=mid-1; else l=mid+1; } return -1;
这里增加了一种情况,那就是a[mid]==key的情况,因为此处我们要精确地查找key,所以在发现a[mid]==key的时候立刻返回mid。
其它的情况都很好理解,如果偏大就在左半边找,否则在右半边找。
这个二分查找看上去很简单,但是,凶险的在后面。
2、查找大于等于/大于key的第一个元素
int l=1,r=n; while (l<r) { int mid=(l+r)/2; if (a[mid]>=key) r=mid; //如果要求大于,可以将=去掉 else l=mid+1; } return l;
怎么样,似曾相识对不对?
我们其实就是在找水平最差的能AK的人,只要把大于等于key第一个元素看做找水平最差的能AK的人,就很好理解了吧?
大于等于可以视为能够AK 。那么,我们按照之前讲到的,如果一个人可以AK(a[mid]>=key),那么比这个人强的人必然可以AK(对于所有i>mid,a[i]>=key),而且不会更优,所以不要,就让r=mid
如果这个人不可以AK(a[mid]<key),那么比他弱的更不行(对于所有i<mid,a[i]<key),就令l=mid+1
只要我们拿之前讲过的找AK的例子来类比一下,一下子就理解了
3、查找小于等于/小于key的最后一个元素
int l=1,r=n; while (l<r) { int mid=(l+r)/2; if (a[mid]<=key) l=mid; //如果求小于,可以去掉= else r=mid-1; } return l;
这里也是一个类比:就是上面讲过的,不能AK的最强选手,这里的“不能AK”指的是小于等于key。
这里,如果一个人可以AK(a[mid]>key,注意,没有等于,因为这里算的是小于等于),那么他和比他强的都不符合条件,此处是r=mid-1
如果他不能AK,那么留下他和比他水平更高的(l=mid)
总结一下,我们只需要把二分查找与之前的AK例子结合起来看,就不会写错边界了。
Part5:二分答案例题——丢瓶盖(洛谷P1316)
简述:地上丢了A个瓶盖,为了简化问题,我们可以当作这A个瓶盖丢在一条直线上,现在要从这些瓶盖里找出B个,使得距离最近的2个距离最大
对应关系:
- 问题——不能AK的最强选手(可以选出B个瓶盖的最大距离)
- 不能AK——可以选出B个瓶盖符合条件
- 水平——最大距离
- 如果居中的那个人不能AK(当前的距离限制可以选出B个瓶盖满足条件),那么令l=mid,留下他和水平更高的(往大了找)
- 如果居中的那个人可以AK(当前的距离限制不允许选出B个瓶盖满足条件),那么令r=mid-1,留下水平更低的
只要能对应起来就很好理解了,下面是示例代码:
#define maxn 100000+500 #include<cstdio> #include<algorithm> using namespace std; int n,k; int a[maxn]; int check(int m) { int tmp=a[1]+m,cnt=1; for (int i=2;i<=n;++i) if (a[i]>=tmp) { cnt++; tmp=a[i]+m; } return cnt>=k; } int main() { scanf("%d%d",&n,&k); int l=1,r=1000000000; for (int i=1;i<=n;++i) scanf("%d",&a[i]); sort(a+1,a+1+n); // for (int i=1;i<=n;++i) printf("%d ",a[i]); printf("\n"); int ans=0; while (l<r) { int mid=(l+r+1)/2; if (check(mid)) l=mid; else r=mid-1; } printf("%d",l); return 0; }
要能找出对应关系,就一定能理解二分答案的精髓
结语
二分就是这样,维护一个当前可行区间,然后,尽量地取到更优,在当前值不可行的情况下牺牲优秀程度。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号