扫描线总结

PS：

• 线段树并不与扫描线绑定，此篇仅讲解更接近原理的 \(n^2\) 做法，线段树做法为基于此做法的时间优化。

扫描线(实则为一种思想)

• 用处：求取图形面积、周长并
• 思想：将整个图形用一条线扫过去，统计扫过一次得到的答案
  

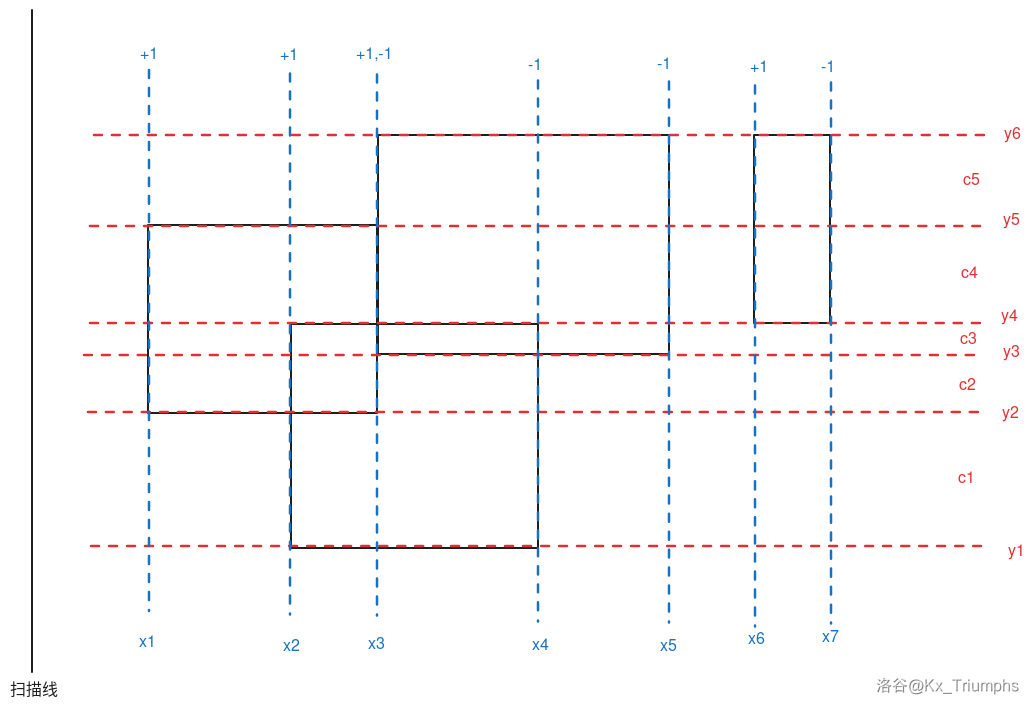
实现过程:

以从左往右扫的矩形面积并为例：

预处理

1. 将每个矩形的两个 \(y\) 坐标离散出来。
2. 记录每个宽的 \(x\) 坐标与 \(y1\) 、 \(y2\) 坐标，并像处理 \(()\) 一样将它们标记为\(\pm 1\) 。
3. 要让线从左至右扫到每条宽，所以宽按 \(x\) 升序排序。

    struct Weith{
        ll x,y1,y2,v;
    }W[N<<1];
    bool cmpW(Weith a,Weith b){
        if(a.x==b.x) return a.v>b.v;//此行有必要，具体见周长并代码
        return a.x<b.x;
    }
    int main(){
        for(int i=1,x1,x2,y1,y2;i<=n;i++){
            cin>>x1>>y1>>x2>>y2;
            //如图中蓝线：左边的宽标为1，进入了矩形；右边的宽标为-1，退出了该矩形
            W[i*2-1]={x1,y1,y2,1};
            W[i*2]={x2,y1,y2,-1};
            //如图中红线：离散y
            y[i*2-1]=y1;
            y[i*2]=y2;
        }
        sort(W+1,w+2*n+1,cmpW);
        sort(y+1,y+2*n+1)
        ll tot =unique(y+1,y+2*n+1)-(y+1);
    }

扫描操作实现

• 实现思路：

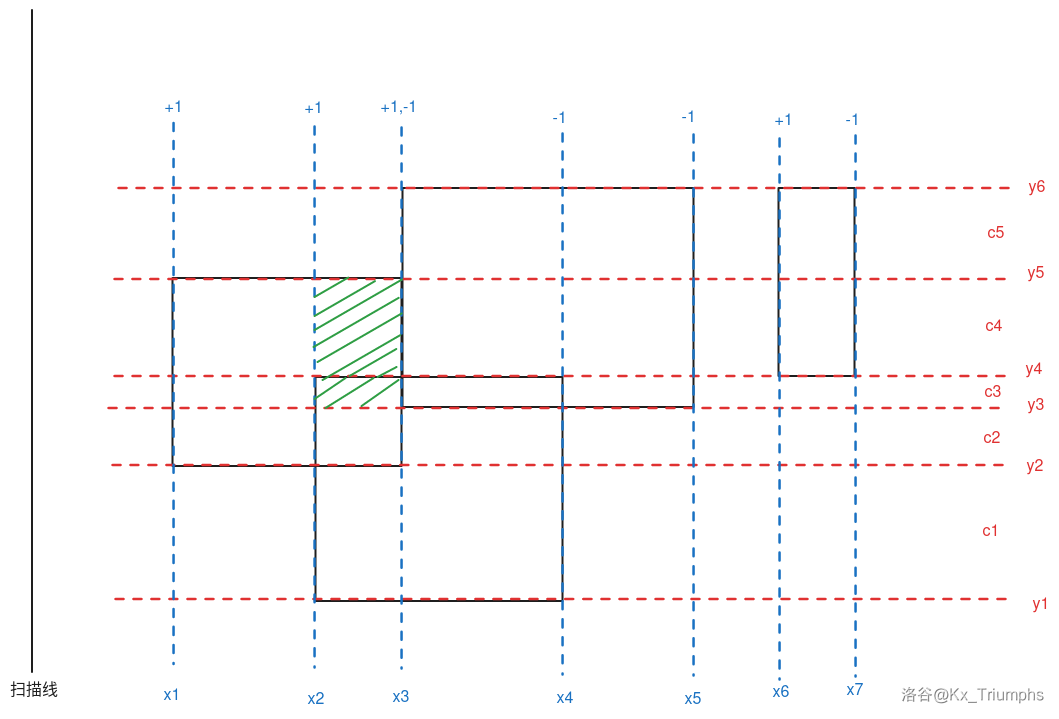
1. \(y\) 已离散，每两个 \(y\) 之间的区间相互不交。对每两个 \(y\) 间的区间记一个 \(c\) ，记录当前区间是否被覆盖。
2. 从左往右枚举每条宽 \(W_i\)，判断每个区间 \(c_j\) 是否被覆盖。
3. 如果该区间被覆盖，统计答案。
   1. 该步骤需在步骤 \(2\) 之前进行。
   2. 如图，枚举到 \(x_3\) 时统计的面积为 \(x_2\) 与 \(x_3\) 之间的 \(\text{\color{green}{绿色阴影}}\) 部分，不能先更改 \(c_j\) 。

    for(int i=1;i<=2*n;i++){
        for(int j=1;j<=tot;j++){
            //统计答案
            if(c[j]>0){
                //x3处重合的两条宽并不会将绿色阴影部分统计两次，因为当枚举到i+1时W[i+1].x-W[i].x=0
                //每个cj对应的范围为 y[j] ~ y[j+1]
                ans+=(W[i].x-W[i-1].x)*(y[j+1]-y[j]);
            }
            //更新cj
            if(W[i].y1<=c[j]&&c[j]<W[i].y2){//下闭上开，不能重复统计
                c[j]+=W[i].v;
            }
        }
    }

矩形周长并：

• 思路：
  • 长宽分别扫一遍(从下往上+从左往右)。
  • 先看宽，对于每个 \(c\)，最外侧的两条才会对答案产生贡献，即在 \(c_j\) 从 \(0\rightarrow1\) 与从 \(1\rightarrow0\) 产生贡献。长同理。
  • 排序细节：如图 \({\text{\color{orange}{橙色}}}\) 部分，两条边重合时，如果先减后加，会使该长度会被统计两次，但实则不应统计。

    struct Weith{
        ll x,y1,y2,v;
    }W[N<<1];
    struct Length{
        ll y,x1,x2,v;
    }L[N<<1];
    bool cmpW(Weith a,Weith b){
        if(a.x==b.x) return a.v>b.v;
        return a.x<b.x;
    }
    bool cmpL(Length a,Length b){
        if(a.y==b.y) return a.v>b.v;
        return a.y<b.y;
    }