算法总结-重链剖分

算法总结 - 重链剖分

概念

• 重儿子（红点）：父节点 \(f\) 的子节点中子树大小最大的儿子。

• 轻儿子（蓝点）：父节点 \(f\) 的子节点中除重儿子以外的节点。

• 重链（橙圈框出的链）：链顶为轻儿子，由重儿子组成的链。

  

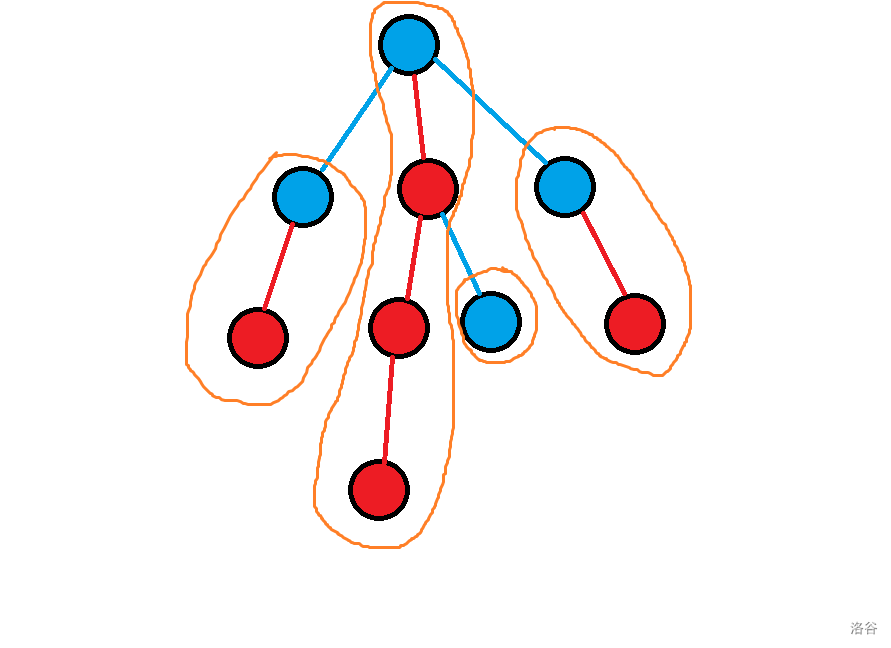
重链剖分

用处：

1. 将树划分成不超过 \(\log{n}\) 条连续的链。
2. 通过节点的 DFS 序，使树上的节点形成一个连续的序列，便于维护树上的修改操作。

实现：

• 第一遍 DFS：

1. \(dep\) 数组：存储每个节点的深度。

2. \(fa\) 数组：存储每个节点的父节点。

3. \(siz\) 数组：存储每个节点的子树大小。

4. \(son\) 数组：存储每个节点的重儿子。

   void dfs1(int x,int f){
       dep[x]=dep[f]+1;
       fa[x]=f;
       siz[x]=1;
       for(int i=0;i<e[x].size();i++){
           int y=e[x][i];
           if(y==f) continue;
           dfs1(y,x);
           siz[x]+=siz[y];
           if(siz[son[x]]<siz[y]) son[x]=y;//更新重儿子
       }
       return ;
   }
   

• 第二遍 DFS：

1. \(top\) 数组：记录每条重链的链顶。

2. \(dfn\) 与 \(val\) 数组（看情况设置这两数组，如求 LCA 就不需要）：

   1. \(dfn\) 数组：记录每个结点搜到的顺序，也就是 DFS 序。

   2. \(val\) 数组：按 DFS 序存储每个节点的点权。

        void dfs2(int x,int t){
        top[x]=t;
        dfn[x]=++did;
        val[did]=a[x];
          if(!son[x]) return ;//没重儿子说明也没有轻儿子
          dfs2(son[x],t);
          for(int i=0;i<e[x].size();i++){
            int y=e[x][i];
            if(y==fa[x]||y==son[x]) continue;
            dfs2(y,y);
        }
        return ;
      }
      

• 主函数：

  • 调用两个预处理重链的 DFS 函数即可。

    注：没有链的链顶为 \(0\)，不可习惯性地写成 \(dfs2(rt,0)\)，应该是 \(dfs2(rt,rt)\)。

运用

树链剖分求 LCA

• 思路：

1. 将深度更深的点跳到链顶的父节点（每次跳跃跳完一整条链，链顶的父亲才是下一条链）。
2. 若跳完后不在同一条链上，重复步骤一。
3. 当两点跳到同一条链上时，此时深度更浅的结点即为 LCA 。

• 复杂度证明：因为已经被划分为 \(\log n\) 条链，所以最多只会有 \(\log n\) 次跳到链顶的父节点，所以单次查询 LCA 的时间复杂度为 \(O(\log n)\)。

• 求 LCA 部分代码：

  void LCA(int x,int y){
  	while(top[x]!=top[y]){//链顶不同，说明不在同一条重链上
  		if(dep[top[x]]<dep[top[y]]) swap(x,y);
          x=fa[top[x]];
      }
      return dep[x]<dep[y]?x:y;//当都在同一条链上时，深度更浅的为节点即lca
  }
  

维护树上操作

原题

• 给一棵树，要求维护以下操作：

1. 将 \(x\) 到 \(y\) 路径上所有节点的权值都加上 \(z\)。

2. 求 \(x\) 到 \(y\) 路径上所有节点的权值之和。

3. 将 \(x\) 的子树内所有节点的权值都加上 \(z\)。

4. 求 \(x\) 的子树内所有节点的权值之和。

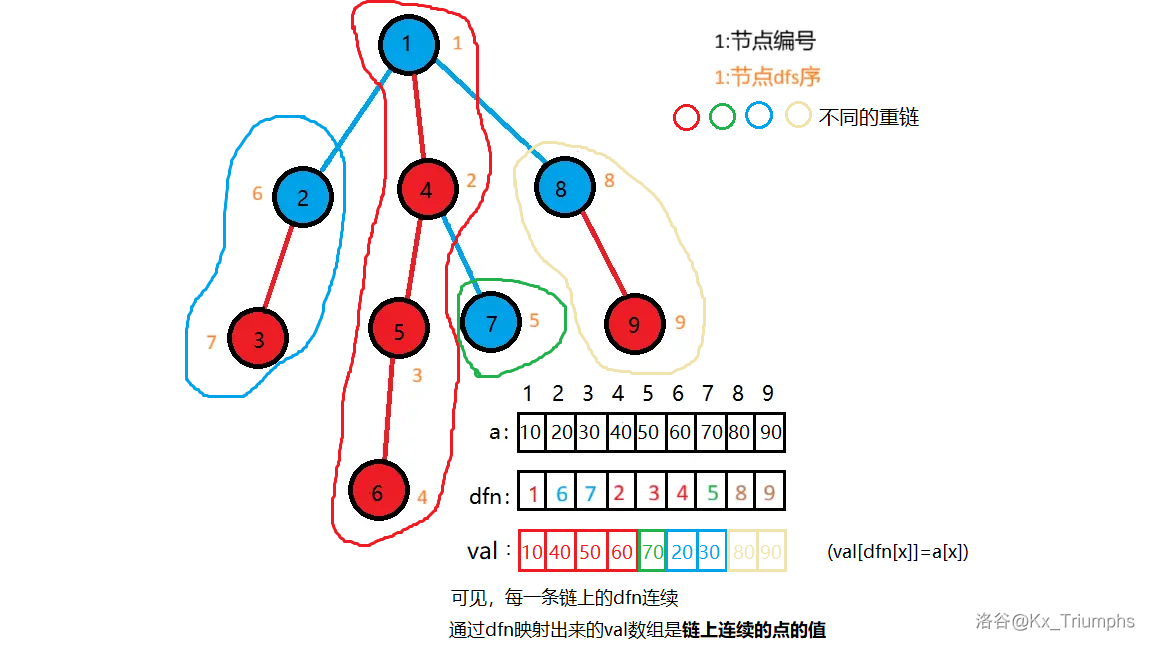
• 思路：将树上的点通过 DFS 序生成一个连续的序列，使用这个新的序列来维护区间操作。

  

• 代码：

  • 映射 \(dfn\) 与 \(val\)：

    void dfs2(int x,int t){
        top[x]=t;
        dfn[x]=++did;
        val[did]=a[x];
        if(!son[x]) return ;
        dfs2(son[x],t);
        for(int i=0;i<e[x].size();i++){
            int y=e[x][i];
            if(y==fa[x]||y==son[x]) continue;
            dfs2(y,y);
        }
        return ;
    }
    

    • 不理解 \(val\) 映射的一定要自己模拟一下（模拟结果在结尾），这里给一组简单样例：

      //样例
      10 20 30 40 50
      1 2
      1 3
      2 4
      2 5
      

  • 建树（注：用新序列建树）：

    void build(int k,int l,int r){
        if(l==r){
            sum[k]=val[l]%Mod;//注意这里用新序列建树
            return ;
        }
        int mid=(l+r)>>1;
        build(k<<1,l,mid);
        build(k<<1|1,mid+1,r);
        sum[k]=(sum[k<<1]+sum[k<<1|1])%Mod;
        return ;
    }
    

  • 先看简单一点的，子树内操作（操作 \(3\) 与 \(4\)）：

    • 操作 \(3\)，修改 \(x\) 子树内点权：

      //一棵子树内dfs序为dfn[x]~dfn[x]+siz[x]-1
      modify(1,1,n,dfn[x],dfn[x]+siz[x]-1);
      

    • 操作 \(4\)，求子树内点权和：

      query(1,1,n,dfn[x],dfn[x]+siz[x]-1);
      

  • 路径上操作（操作 \(1\) 与 \(2\)）：

    • 操作 \(1\)，修改 \(x\) 到 \(y\) 路径上点权：

    void tree_modify(int x,int y,int v){
        while(top[x]!=top[y]){
            if(dep[top[x]]<dep[top[y]]) swap(x,y);//和求LCA一致
            modify(1,1,n,dfn[top[x]],dfn[x],v);//修改对应的新序列中的值
            x=fa[top[x]];
        }
        //当跳到同一条链上后，x、y未必是同一点，之间的这一段也需修改
        if(dep[x]<dep[y]) swap(x,y);
        modify(1,1,n,dfn[y],dfn[x],v);
        return ;
    }
    

    • 操作 \(2\)，查询 \(x\) 到 \(y\) 路径上点权和：

    int tree_query(int x,int y){
        int ans=0;
        while(top[x]!=top[y]){
            if(dep[top[x]]<dep[top[y]]) swap(x,y);
            ans+=query(1,1,n,dfn[top[x]],dfn[x])%Mod;//同修改
            x=fa[top[x]];
        }
        //同修改
        if(dep[x]<dep[y]) swap(x,y);
        ans+=query(1,1,n,dfn[y],dfn[x])%Mod;
        return ans%Mod;
    }
    

    //上述样例模拟结果
    u:   1  2  3  4  5
    a:  10 20 30 40 50
    dfn: 1  2  5  3  4
    //val[dfn[u]]=a[u]
    val:10 20 40 50 30
    

发现一处错误：图树链剖分 - dfs 序 on 2025.10.25，待修改。

update on 2025.10.26，修改了笔误与错误图片，更新和优化了理解性内容，补全了操作 \(3\) 与 \(4\)。

To Be Continue