算法总结-字典树(Trie树)

算法总结-字典树( \(Trie\) 树)

用处：

由字典序与字符构成的树，常用于处理字符串，时间复杂度一般为 \(O(|S|)\)。

普通 \(Trie\) 树：

• 一般以字符为边，也可以作为点处理，这里以点建树。

• 每一层最多只有字符集的个数个节点，同一字符在每层只会有一个节点或边。如字符串 \(abcd\) 与 \(abdc\) 会建成如下一图：

  

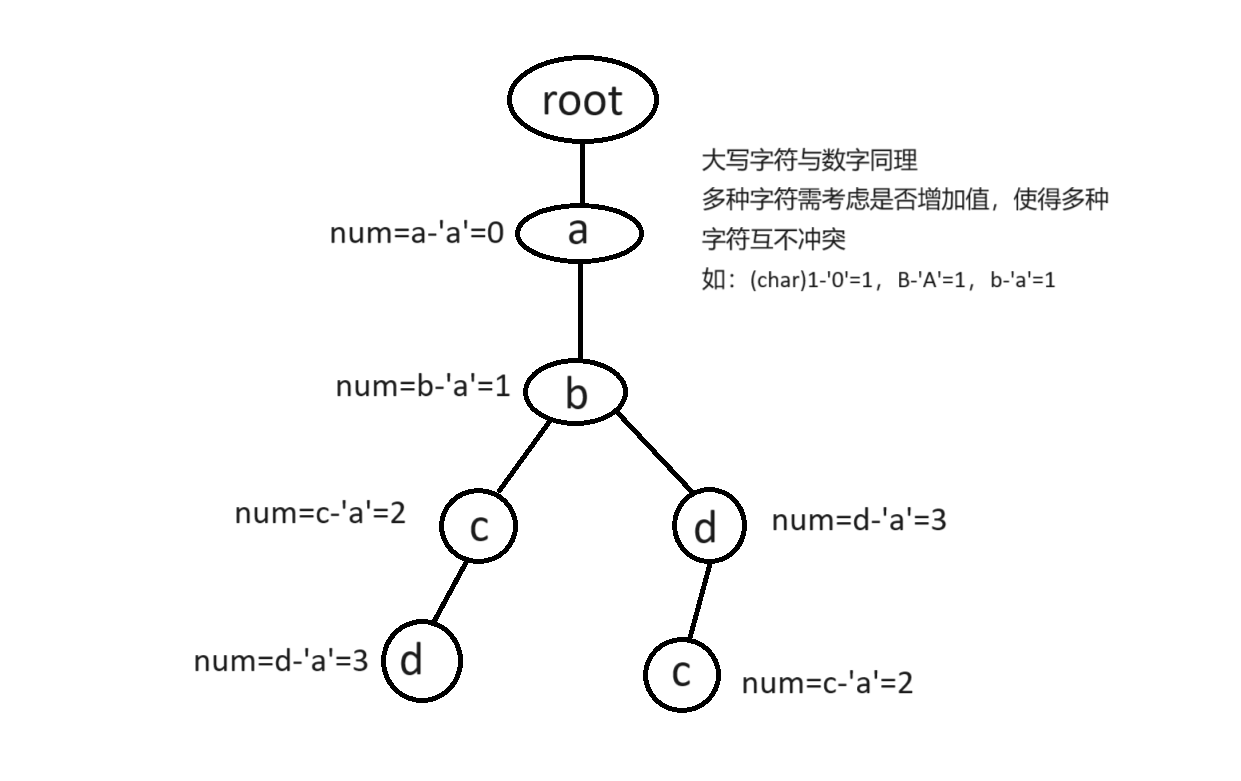
  • 建树代码

    void build(string a){
    	int pos=0,c;
    	for(int i=0;i<a.size();i++){
            if(a[i]>='a'&&a[i]<='z') c=a[i]-'a';
    		else if(a[i]>='A'&&a[i]<='Z') c=a[i]-'A'+26;
    		else if(a[i]>='0'&&a[i]<='9') c=a[i]-'0'+52;
    		if(tr[pos][c]==0){
    			tr[pos][c]=++tid;
    		}
    		pos=tr[pos][c];
    	}
    }
    

• \(0/1Trie\) 树：

  • 每层最多有两个点( \(0/1\) )，常用于解决异或和，异或路径等问题。可以分情况从高位到低位或者从低位到高位建树（这里以高位到低位建树）。

  • 如 \(7\) 与 \(10\) 两数的二进制为 \(111\) 与 \(1010\) ，那么它们就会建成如下图的字典树：

    

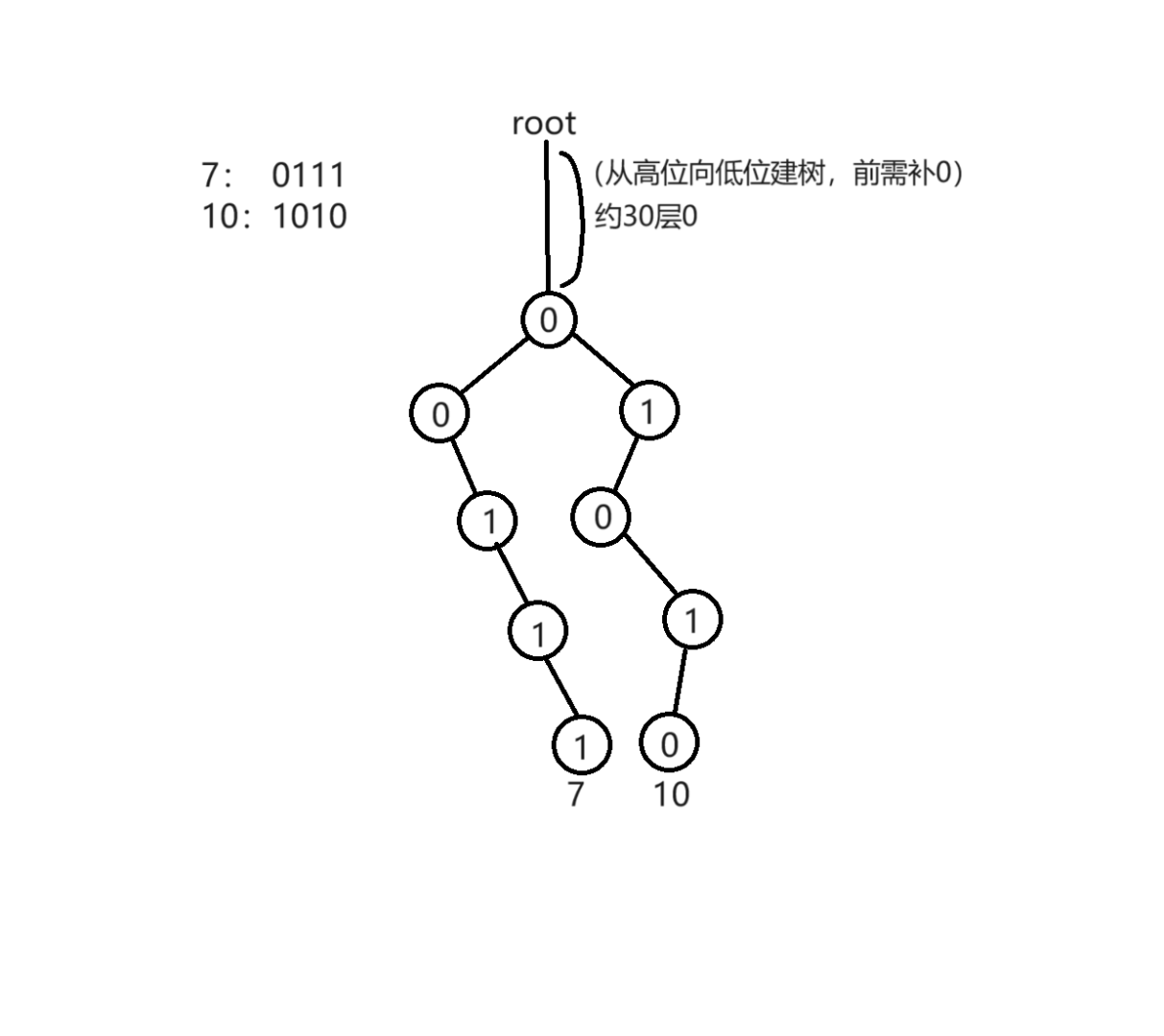
  • 建树代码：

    void build(int a){
    	int pos=0;
    	for(int i=31;i>=0;i--){
    		//a的二进制中从低到高第i位的值  
    		int c=(a>>i)&1;
    		if(tr[pos][c]==0){
    			tr[pos][c]=++tid;
    		}
    		pos=tr[pos][c];
    	}
    	return ;
    }
    

  • P4551 最长异或路径

    • 思路：递归 \(0/1Trie\) 树，求出每个点到根的异或和，每次取到当前点 \(pos\) 的值 \(c\) （ \(a\) 二进制中第 \(pos\) 位的值）。如果当前点有一条路径与 \(c\) 异或后能变得更大，那么就选这条路径（贪心思想）。

    • 正确性证明：

      1. 两点的 \(LCA\) 以上的节点都是 \(0\)，然而 \(0\oplus 0=0\)，不会对本身异或和的答案造成影像。
      2. 一个数 \(10000\) 在第二位分别与 \(0\) ，\(1\) 异或，得出 \(10000\) 与 \(11000\) 。可以发现，即使与 \(1\) 异或后每位都得出 \(0\) （\(11000\)） ，也比与 \(0\) 异或后每位都得出 \(1\) (\(10111\)) 要大。

    • 求路径代码：

    void dfs(int x,int fa){
    	for(int i=0;i<e[x].size();i+=2){
    		int y=e[x][i],w=e[x][i+1];
    		if(y==fa) continue;
            //递归求出每个数到根节点(root)的异或和
    		dis[y]=dis[x]^w;
    		dfs(y,x);
    	}
    	return ;
    }
    int query(int a){
    	int pos=0,sum=0;
    	for(int i=31;i>=0;i--){
    		int c=(a>>i)&1;
    		if(tr[pos][!c]){
    			sum+=(1<<i);
    			pos=tr[pos][!c];
    		}
    		else pos=tr[pos][c];
    	}
    	return sum;
    }
    int main(){
        ...
        for(int i=1;i<=n;i++){
    		ans=max(ans,query(dis[i]));
        }
        ...
    }