假设(基于二维)
训练集
\[\begin{bmatrix}
1&x_{11}&{\cdots}&x_{1n}\\
1&x_{21}&{\cdots}&x_{2n}\\
{\vdots}&{\vdots}&{\ddots}&{\vdots}\\
1&x_{m1}&{\cdots}&x_{mn}\\
\end{bmatrix}*
\begin{bmatrix}
\theta_{0}\\
\theta_{1}\\
{\vdots}\\
\theta_{n}\\
\end{bmatrix}=
\begin{bmatrix}
y_{1}\\
y_{2}\\
{\vdots}\\
y_{n}\\
\end{bmatrix}
\]
表达式
\[h_\theta(x)=\theta_0+\theta_1x_1+...+\theta_nx_n...x为向量
\]
定义代价函数
\[J_\theta(\theta_0,\theta_1,\theta_2,...,\theta_n)=\frac{1}{2m}\sum_{i=1}^{m}({h_\theta(x^i)-y(x^i)})^2
\]
梯度下降法
\[min_{\theta_0...\theta_n}J(\theta_0,\theta_1,\theta_2,...,\theta_n)
\]
\[\theta_j=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1,\theta_2,...,\theta_n)...\alpha为学习率
\]
故
\[\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1,\theta_2,...,\theta_n)=\frac{1}{m}\sum_{i=1}^{m}({h_\theta(x^i)-y(x^i)})x^i
\]
带入得
\[\theta_j=\theta_j-\alpha\frac{1}{m}\sum_{i=1}^{m}({h_\theta(x^i)-y(x^i)})x^{ij}
\]
梯度下降法实现
定义精度为P
\[当\theta_j^n-\theta_j^{n-1}<=P时递归停止
\]
初始化
\[(\theta_0,\theta_1,\theta_2,...,\theta_n)为(0,0,0,...,0)或者其他
\]
执行递归
\[\theta_j一步一步变化直到达到J(\theta)最小值
\]
为什么可以实现？
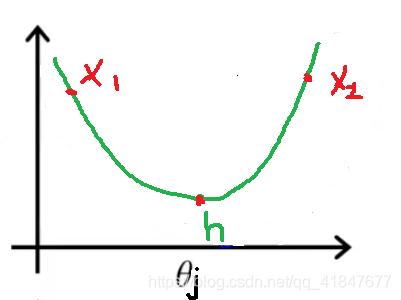
该图为取\((\theta_0...\theta_{j-1},\theta_{j+1}...\theta_n)为固定值时J(\theta)的切片\)
当
\[\theta_j=x_1时\frac{\partial}{\partial\theta_j}J(\theta)<0故\theta_j增加逐渐靠近h，同时精度P决定递归是否停止
\]
当\(\theta_j=x_2时同理\)
学习率\(\alpha\)
过大导致可能不收敛
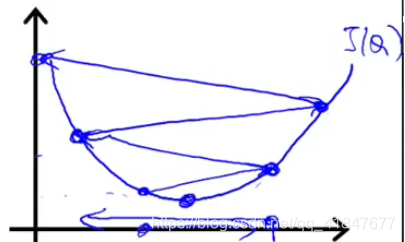
过小导致收敛太慢
故多次实验，取合适的\(\alpha\)
\[\alpha=\begin{bmatrix}0.001&0.01&0.1&1&10\\\end{bmatrix}
\]
特征缩放
\[\begin{bmatrix}x_{1i}\\x_{2i}\\{\vdots}\\x_{ni}\\\end{bmatrix}=\begin{bmatrix}1000\\1001\\{\vdots}\\1020\\\end{bmatrix}->1000*\begin{bmatrix}1.000\\1.001\\{\vdots}\\1.020\\\end{bmatrix}
\]
若\(h_\theta=\theta_0+\theta_1x_1^2+\theta_1x_2^3+...\)
可令$$x_12=t_1,x_23=t_2...$$ 即可实现
正则方程实现
\[\theta=(X^TX)^{-1}X^TY...(X^T为X的转置，X^{-1}为X的逆)
\]
浙公网安备 33010602011771号