关于走楼梯问题的背包算法和递归算法

递归算法

public class question15 {
public static void main(String args[]){
System.out.println(climbStairs(45));
}
public static int climbStairs(int n){
if (n==1)
return 1;
if (n=3)
return n;
return climbStairs(n-1)+climbStairs(n-2);
}
}

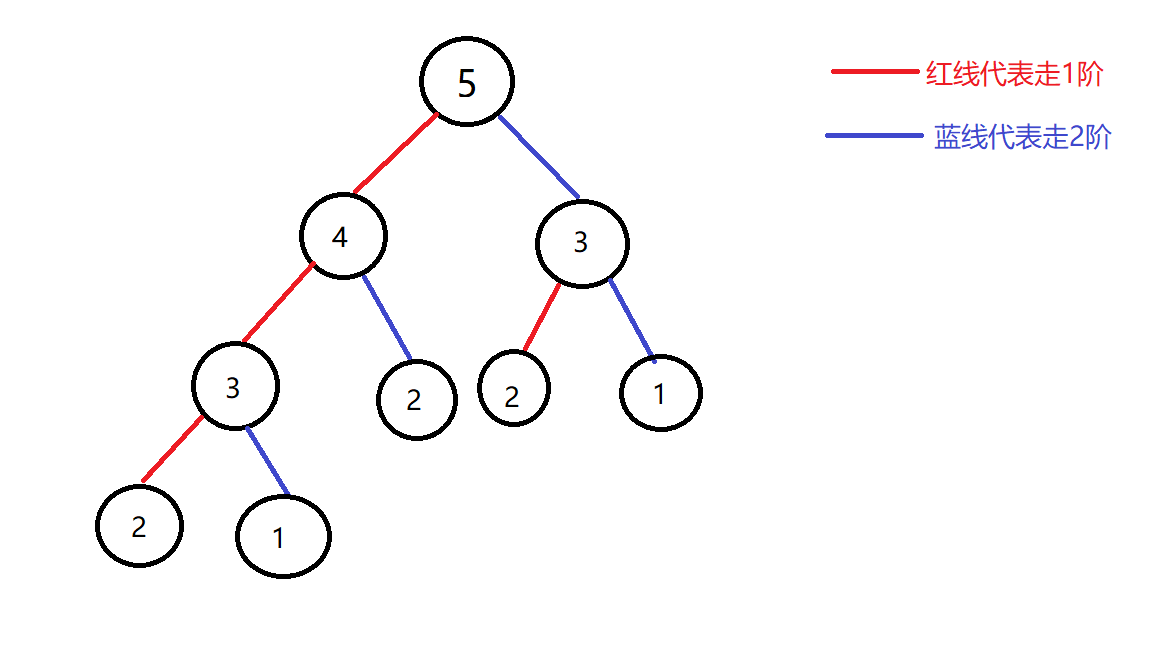
如图所示
我们假设有一个函数F(当然要自己写)这个函数的作用就是可以求出有多种方式上n层楼
那么可以得出F(5) = F(4) + F(3)
推广可得 F(n) = F(n-1) + F(n-2)
如果上一层台阶的话只有1种上法(一次走一阶)
如果上两层台阶的话有2种上发(一次走一阶走两次,或者一次性走两阶)
可以得到F(2)=2 F(1) = 1
拿上图的3进行举例来说 F(3) = F（2）+ F（1）
可得 F（3）= 3
由此我们就可以推出递归关系了
即把任意一个数分别通过-1 -2 的两种方式,一直减到出现F(1)和F(2)的时候再重新进行回溯

动态规划(背包算法)

如果说递归算法可以看成从大的递推到小的再回溯的话
那么动态规划可以看成是从小的直接推到大的 所以更加节省时间
动态规划也是一种带有"记忆力"的算法 就是一样东西算过之后不会再重复第二遍
先上代码:
public static int climbStairs2(int n) {
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}

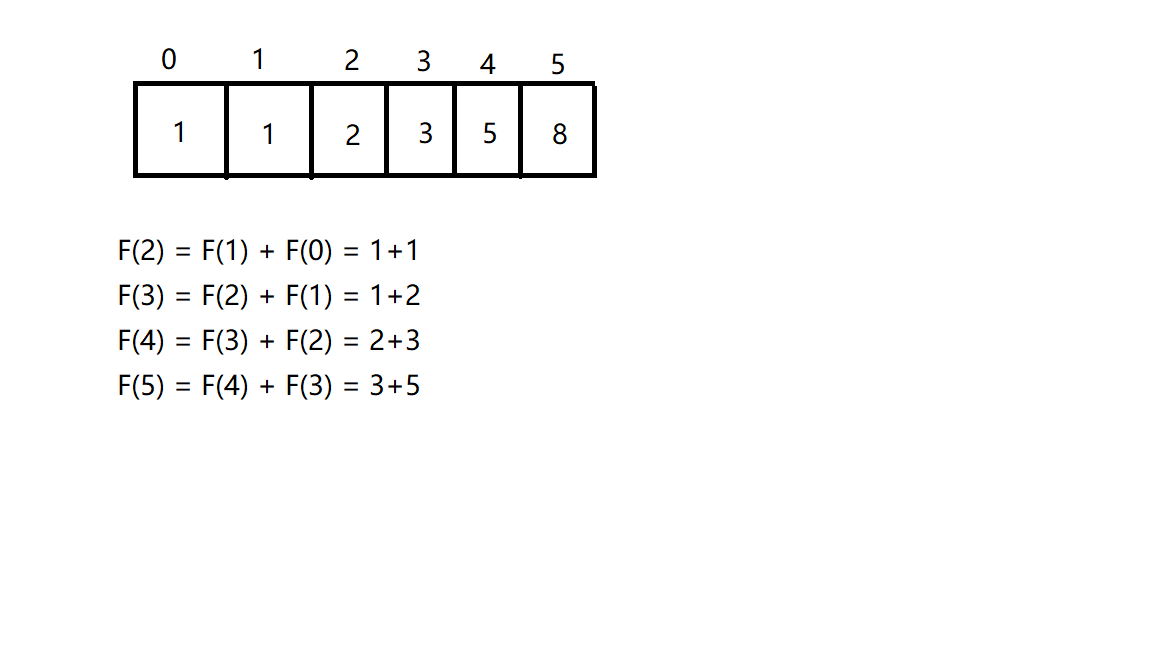
如图所示该算法的核心就是把前面的用到后面上
如果按照第一种的思路:
F(4) = F(3）+ F（2）= F(2) + F(1) + F(2)
但是在动态规划种可以直接使用F(3) 的数值 因为是有"记忆的"
由此也节省了大量的内存
最后一提台阶数为5的时候上楼梯的方法都是 8

如有问题欢迎指正