算法--排序和搜索
排序和搜索算法
排序是指将元素按照一定规则进行顺序排列,通常有两种排序的方式,升序排序和降序排序。例如我我们有一组元素{5,2,7,1},对该组数据进行升序排序,结果为{1,2,5,7},对其进行降序排序结果为{7,5,2,1}。排序的目的是为了可以使得数据可以以更好的更有意义的形式的表现出来。虽然排序最显著的应用是以排序的数据来对其进行显示。但是往往在许多应用场景被使用作为算法的一部分。
总的来说,排序的算法可以分为两个大类:比较排序和线性时间排序。比较排序依赖比较和交换将元素的移动到正确的位置上,但是这不一定,不是所有的排序算法都是依赖比较。而且对于那些依赖于比较进行排序的算法,其算法的时间复杂度不可能小于\(O(NlgN)\)。对于线性排序而言,很明显我们可以通过的名字看出,它的算法复杂度为O(N)。但是遗憾的是,线性排序依赖于数据集合中某些特征,不可能在所有的场合都可以使用。某些排序算法只使用数据本身的存储空间进行数据的存储,这些算法方式我们称之为就地排序,有的排序需要开辟额外的空间来对数据进行处理。
搜索算法,就是在一堆数据集合中找到一个元素的位置,一种最简单的方式,就是将数据所有的数据遍历一遍,这就是所谓线性搜索。通常而言线性搜索对随机访问支持不是太好的数据结构中,例如链表。另外一种就是二分查找,这个在本文章会进行说明。当然还有一些数据结构是专门用于查找,比如二叉搜索树和哈希表等。
插入排序
插入排序是最简单的排序算法。它的工作方式类似我们在整理一堆写有随机数字的纸条,这时一边有一堆没有进行排序的纸条,另外一边是有一块空地放置已经排序好的纸条,每一次我们在未排序的纸条堆中取一张,并且根据数字将它放在有序的纸条的正确位置。比较学术的表示为:插入排序每次从无序数据集合中取出一个元素,扫描已经排序的数据集合,并且将它插入有序集合的合适位置上。尽管简单一看,插入排序需要两堆数据集大小的空间,但是实际上并不需要额外空间。
插入排序在思维上来说是一种简单的排序算法,但是它在处理大量的数据的效果并不高效,很明显,在插入数据到有序数据集前,要将插入的数据和有序数据集合中的其他的数据进行对比,随着数据集的变大额外的开销也会变大,然而插入排序的优点,当元素插入到一个有序的数据集合中,只需要对数据集合最大一次的遍历,而不需要完整的运行算法。
插入算法的接口定义
issort
int issort(void **data, int size, int esize, int (*compare)(const void *key1, const void *key2))
返回值:如果排序成功,返回0;否则返回-1
描述:利用插入排序的将给定数据进行排序。data中的元素个数由size决定,而每一个元素的大小的由esize决定。函数指针compare会指向一个用户定义的函数来进行比较元素的大小,
时间复杂度:\(O(n^2)\) n为要排序的元素的个数
插入排序的实现分析
插入排序从根本上而言,就是每次从未排序的数据集合中找到一个元素,插入到已经排序好的数据集合中。在下图中我们来实现一个插入排序的算法。两个数据都是存放到data当中,data是一块连接好的存储区域。最初,data中包含size个元素,随着issort的运行,data逐渐被有序的数据集合取代,直到排序函数完成。虽然实现插入排序我们的例子是使用一块连续的空间,但是的实际上使用链表也是可以实现插入排序的。并且两者效率都不差。
插入排序使用循环来进行排序,外部的循环用j来控制元素,使得元素从无序的数据集合中插入到有序的集合中。由于待插入的元素总是在有序集合的右边,所以我们可以理解j为分隔有序集合和无序集合的分界线。对于每一个j指向的元素,都是使用变量i来遍历元素应该放置的有序集合中的位置。
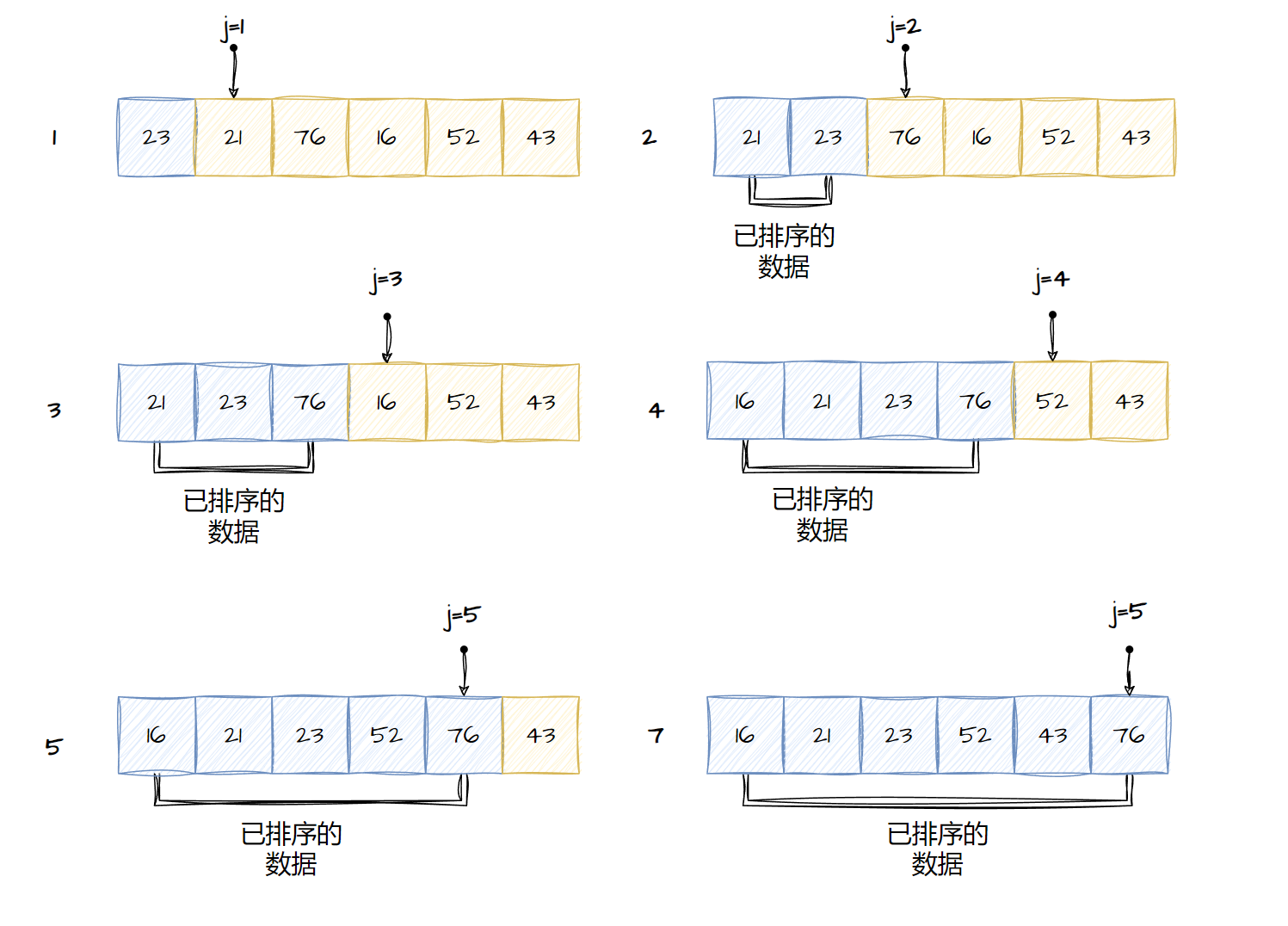
插入排序的时间复杂在于它的嵌套的循环部分。考虑到这一个原因,外部循环的运行时间为\(T(n) = n -1\),其\(n\)为要排序的元素的个数。而内部的循环,可以考虑在最坏的情况,需要遍历所有有序的数据才可以插入到正确的位置中,所以内部的循环的次数为1到\(n-1\)的集合\(T(n) = (n*(n+1))/2\),所以使用算法的\(O\)表示方法简化为\(O(n^2)\)。当一个已经排序的好的数据中使用插入排序,其时间复杂度为\(O(n)\)。插入排序不需要新增排序空间,直接使用无序数据集合的空间即可。
插入排序的代码实现
int issort(void *data, int size, int esize, int (*compare)(const void *key1, const void *key2))
{
char *temp = data;
void *key = NULL;
int j = 0;
int i = 0;
/* 分配内存给key元素 */
if((key = (char*)malloc(esize)) == NULL)
return -1;
for(j = 1; j < size; ++j)
{
memcpy(key, &temp[j*esize], esize);
i = j - 1;
while(i >= 0 && (compare(&temp[i* esize], key) > 0))
{
memcpy(&temp[(i+1) * esize], &temp[i * esize], esize);
i--;
};
memcpy(&temp[(i+1) * esize], key, esize);
}
free(temp);
return 0;
}
快速排序
快速排序是一种分而治之的算法,一般而言它被认为一种大多场景最佳的排序算法。如果插入排序一样,快速排序也是一种比较排序,并且也不需要多余的存储空间。在处理大型的数据集合中,快速排序是一种比较好的排序选择。
同样我们使用一堆乱序的写有数字的纸条举例子,我们可以将未排序的纸条分成两堆。其中一堆的专门放置小于或者等于某一个数字的纸条,另外一堆的用来放置大于这个数字的纸条。我们通过这种方式得到了两堆支票后,又可以通过同样的方式将他们分成四堆,重复这种方式,最后我们可以得到每一个堆中只有一张纸条的情况,那这个时候,我们纸条就已经排序完成了。
由于快速排序是一种分而治之的算法,因此我们可以将其步骤分为三个步骤,这样就有助于我们进行理解。
- 分:设定一个分割值并且将数据分为两个部分
- 治:分别在两边使用递归的方式继续进行快速排序法
- 合:对分割的部分排序直至完成
这里必须注意一点,快速排序的最坏的性能并不会比插入排序的最坏的性能来的好。但是我们可以选择合适的分割值来使得其表现和平均情况相当。所以分割值对于快速排序是很重要的。
如果选择的分割值将大部分的元素都放在其中一堆中,那么此时快速排序的性能就会很差。所以选择分割值应该尽量的将元素平均分割开。举一个例子,使用10作为{15,20,18,51,36,10,77,43}的分割值,其结果就是将数据集合分为{10},{15,20,18,51,36,10,77,43},明显不平衡,但是如果选择分割值为{36},其结果为{15,20,18,10}和{36,51,77,43},这样就相对的比较平衡。
选择分割值的一种方式就是使用随机的选择法进行选取。同时,还可以改进这种随机的方式,方法就是随机选择三个元素,然后在三个元素中选择中间值。这种就是中位数法。由于这种分割方式依赖数据集合的随机性从而保证快速排序的整体的性能,因此快速排序作为随机算法的比较适用的算法。
快速排序算法的接口定义
int qksort(void data, int size, int esize, int i, int k, int (compare)(const void* key1, const void* key2))
返回值:如果排序成功,返回0;否则返回-1
描述:利用快速排序将数组的进行排序。数组中的元素个数由size决定。而每一个元素的大小由esize决定。参数i和参数k决定当前排序的两个部分,其值分别为初始值0和size-1。函数指针compare会指向一个用户定义的函数来比较元素的大小。
时间复杂度:\(O(nlgn)\) n为要排序的元素的个数。
快速排序的实现和分析
快速排序的本质上来说是不断的将无序元素进行递归分割,直到所有的元素都变为有序的。在以下的实现中,数据集合中存在size个无序的元素。并且存放在连续的存储空间当中,快速排序就不需要额外的存储空间,所以所有的分割过程都在数据集合中,当分割完成后,数据集合中就完成一个有序的集合了。
这里有一个很关键的部分就是如何进行数据的分割,这个部分我们使用一个函数partition来实现, 具体的实现我使用以下图进行表示。
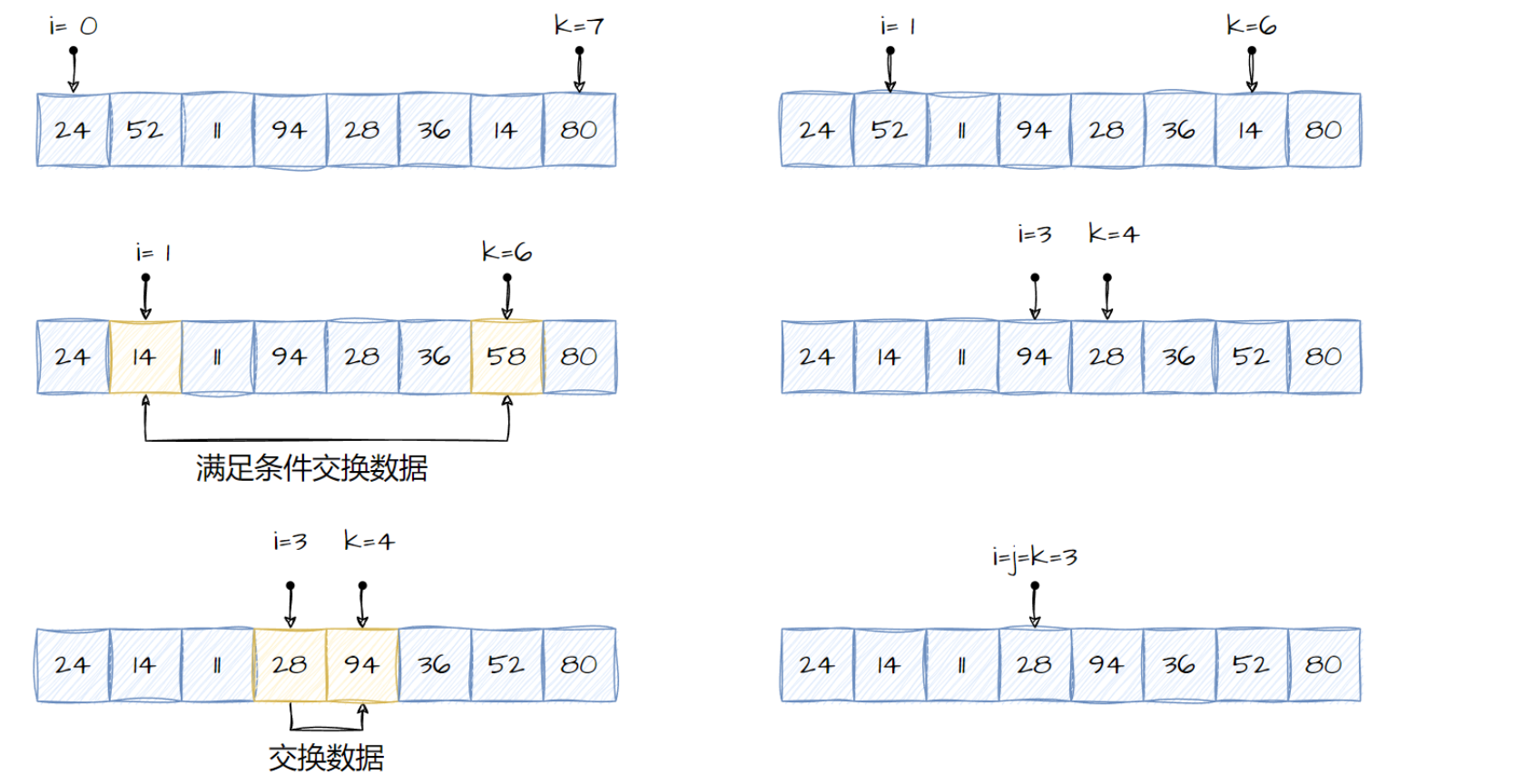
首先用之前提过的中位数选取一个分割值。一旦分割值确定了,就将k往数据的左边移动,直到找到一个小于或者等于分割值的元素。这个元素属于左边分区,接下去,将i往右边移动,直到找到一个大于或者等于分割值的元素。这个元素属于右边分区。一旦找到两个元素属于错误的位置,就交换两者的分区,总会存在一个可以用来交换的元素在另外的一个分区。一旦i和k重合,那么所有处于左边的元素将小于等于它,所有处于右边的值将大于等于它。
现在我们来分析一下qksort中如何处理递归的数据。在第一次调用qksort函数时,i的值置为0,k的值置为size-1。首先调用partition函数将data中处于i和k之间的元素进行分区。当partition返回时,将j赋予分割点的元素。接下来,递归调用qksort来处理左边的分区从i到j。左边的分区继续递归直到传入qksort中的分区只存在单个元素。同理,分区的右边也进行递归处理,处理的区间为j+1到k。简而言之,通过这种递归方式,直到首次达到qksort终止的条件,这个时候,数据就完全排序好。
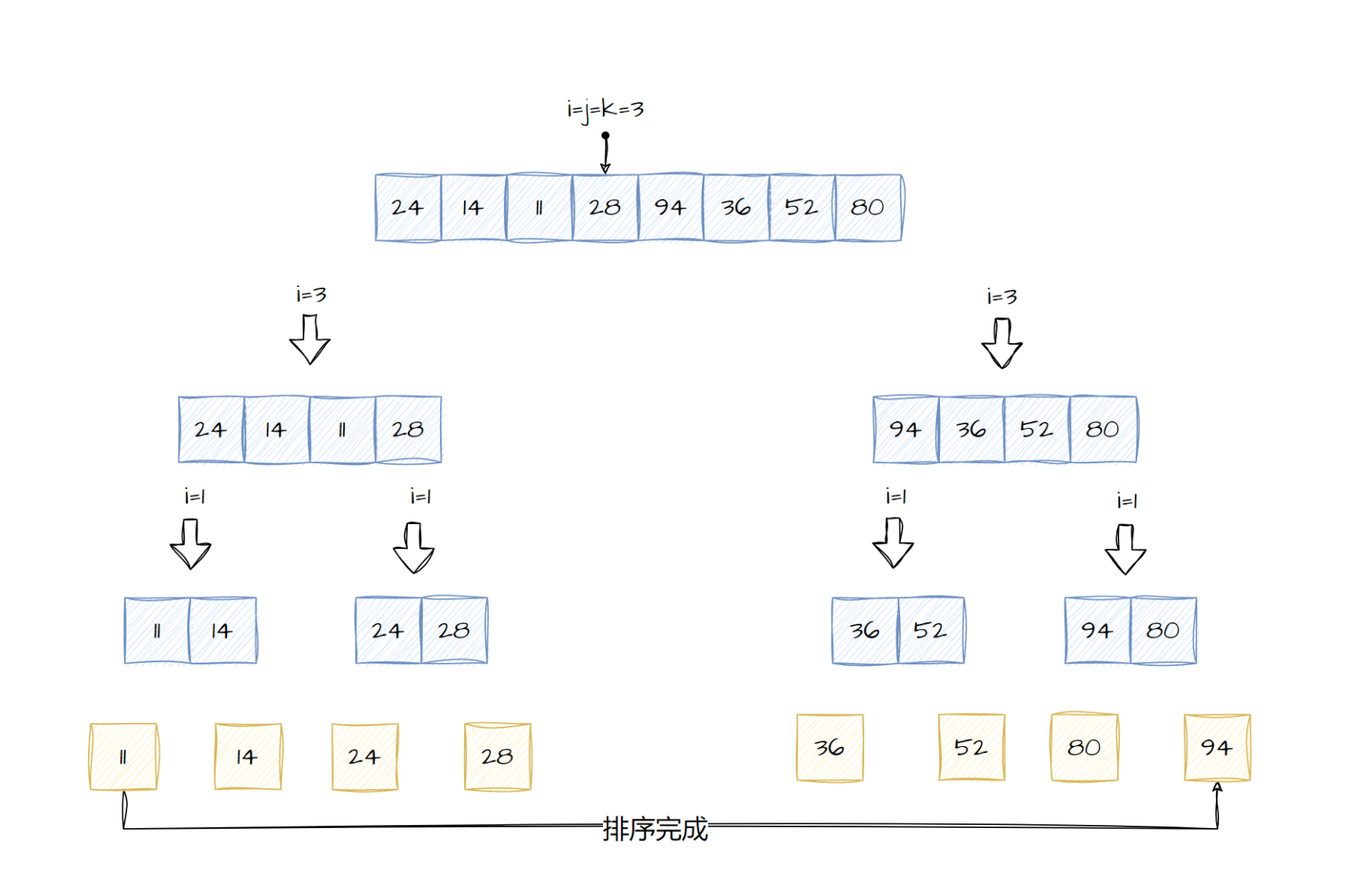
在分析快速排序的性能,我们通常时围绕着平均性能进行分析,因为一致认为平均情况是它复杂度的度量。虽然在最坏的情况下。快速排序的时间复杂度为\(O(n^2)\),并没有插入排序来的迅速,但是快速排序的性能一般情况是比较有保障接近平均性能的。
快速排序的平均性能在平均的情况下取决于数据是否平衡分区是否平衡。如果使用中位数法,那么分区的平衡存在保证,在这种情况下最快就是类似树的遍历速度\(O(lgn)\)的时间复杂度。
static int compare_int(const void* int1, const void* int2)
{
if(*(const int*)int1 > *(const int*)int2)
return 1;
else if(*(const int*)int1 < *(const int*)int2)
return -1;
else
return 0;
}
static int partition(void *data, int esize, int i, int k, int (*compare)(const void* key1, const void* key2))
{
char *a = data;
void *pval;
void *temp;
int rand_value[3];
if((pval = malloc(esize)) != NULL)
{
return -1;
}
if((temp = malloc(esize)) != NULL)
{
free(pval);
return -1;
}
/* 产生三个随机数后选择中位数 */
rand_value[0] = (rand() % (k-i+1)) + i;
rand_value[1] = (rand() % (k-i+1)) + i;
rand_value[2] = (rand() % (k-i+1)) + i;
issort(rand_value, sizeof(int), compare_int);
memccpy(pval, &a[rand_value[1]*esize], esize);
i--;
k++;
while (1)
{
do
{
k--;
}while(compare(&a[k*esize], pval) > 0);
do
{
i++;
}while(compare(&a[k*esize], pval) < 0);
if(i >= k)
{
break;
}
else
{
memcpy(temp, &a[i*esize], esize);
memcpy(&a[i*esize], &a[k*esize], esize);
memcpy(&a[k*esize], &a[i*esize] ,esize);
}
}
free(temp);
free(pval);
return k;
}
int qksort(void *data, int size, int esize, int i, int k, int (*compare)(const void* key1, const void* key2))
{
int j = 0;
while(i < k)
{
if(j = partition(data, esize, i, k, compare) < 0)
return -1;
if(qksort(data, size, esize, i, k, compare) < 0 )
return -1;
i = j + 1;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号