通过简单的例子了解逻辑回归算法

通过简单的例子了解逻辑回归算法

Logistic回归是进行分类的基础工具之一。作为数据处理人员，我希望能做很多分类。因此，我认为举例子可以更好地了解Logistic回归如何在更深层次上发挥的作用

当然不推荐这样做：

from sklearn.linear_model import LogisticRegression

++++投篮训练
假设我想研究篮球投篮准确度和我的投篮距离之间的关系。更具体地说，我想要一个模型，以英尺为单位计算“距篮筐的距离”，并指出我进行投篮的概率。

首先，我需要一些数据。因此，我在记录每个结果的同时投了不同距离的篮球（1个代表成功，0个代表失误）。在散点图上绘制时，结果如下所示：

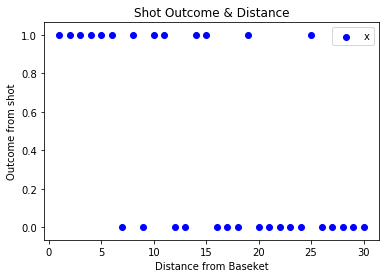
通常，我距离篮筐越远，投篮的准确率就越低。因此，我们已经可以看到模型的大致轮廓：给定较小的距离时，它应该预测较高的概率；给定较大的距离时，它应该预测较低的概率。
在高层次上，逻辑回归的工作原理与线性回归非常的相似。因此，让我们从熟悉的线性回归方程式开始：

Y = B0 + B1 * X

在线性回归中，输出Y与目标变量（您要预测的变量）的单位相同。但是，在逻辑回归中，输出Y为对数赔率。现在，除非您花费大量时间进行体育博彩或在赌场里玩，否则您对赔率的了解可能不是很熟悉。赔率只是表达事件概率P的另一种方式。

赔率= P（事件）/ [1-P（事件）]

继续我们的篮球主题，比方说，我投篮100次，罚球70次。根据这个样本，我罚球的概率是70％。我罚球的几率可以计算为：

P(概率)= 0.70 /（1-0.70）= 2.333

概率限制在0和1之间，这将是回归分析中的问题。如您所见，这里赔率范围是从0到无穷大。

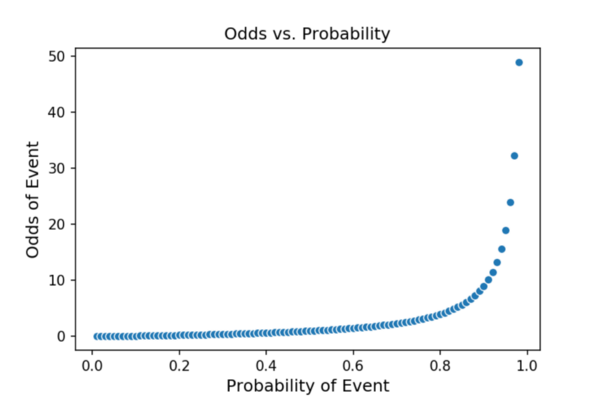
如果我们采用赔率的自然对数，那么我们得到的对数概率无限的（从负无穷大到正无穷大），并且在大多数概率上都是线性的！因为我们可以通过逻辑回归来估计对数几率，所以我们也可以估计几率，因为对数几率只是用另一种方式表示的概率。

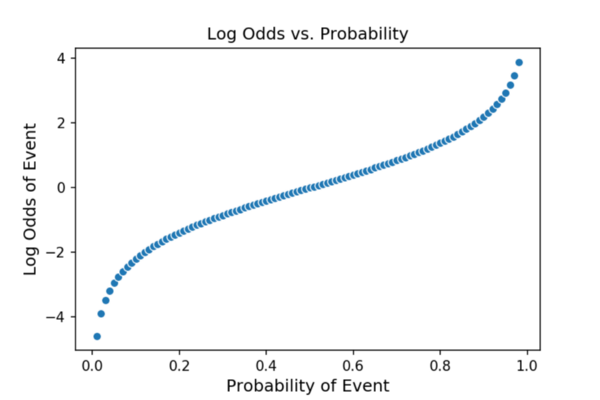
我们可以写出逻辑回归方程：

Z = B0 + B1 *距离篮筐
其中Z = log（odds_of_making_shot）

为了从Z中获得对数赔率的概率，我们应用Sigmoid函数。应用Sigmoid函数是描述以下转换的一种好方法：

投篮的概率= 1 / [1 + e ^（-Z）]

现在，我们了解了如何从对数几率的线性估计变为概率，现在让我们研究一下如何在用于计算Z的对数回归方程中实际估计系数B0和B1。这里的幕后有一些数学运算，但是我会尽力用简单的方法来解释它，以便您（和我）都能对该模型有一个直观的了解。

++++成本函数
像大多数统计模型一样，逻辑回归试图使成本函数最小化。因此，让我们首先考虑一下成本函数。成本函数试图衡量您的错误程度。因此，如果我的预测是正确的，那么就不会有成本，如果我只是一点点错，那就应该是很小的成本，而如果我错了很多，那就应该有很高的成本。在具有连续目标变量的线性回归世界中，这很容易可视化（并且我们可以简单地平方出实际结果与我们的预测之间的差，以计算出每个预测对成本的贡献）。但是在这里，我们正在处理仅包含0和1的目标变量。别失望，我们可以做一些非常相似的事情。
在我的篮球示例中，我从篮筐正下方进行了第一次投篮-即[投篮结果= 1 | 到篮子的距离= 0]。是的，我并不完全喜欢篮球。我们如何将其转化为成本？
首先，我的模型需要吐出一个概率。假设它估计为0.95，这意味着它希望我从0英尺处击中95％的命中率。
在实际数据中，我仅从0英尺处拍摄了一张照片，因此我从0英尺处的实际（采样）精度为100％。采取那个愚蠢的模型！
因此该模型是错误的，因为根据我们的数据，答案是100％，但预测为95％。但这只是轻微的错误，因此我们只想对它进行一点惩罚。在这种情况下，惩罚为0.0513（请参阅下面的计算）。请注意，仅将实际概率与预测值之差接近。另外，我想强调的是，此错误与分类错误不同。假设默认截止值为50％，则该模型将正确预测1（因为其95％> 50％的预测）。但是该模型不是100％肯定我会做到，因此我们对其不确定性只加了一点惩罚。

-log（0.95）= 0.0513

现在，我们假设我们建立了一个糟糕的模型，它的概率为0.05。在这种情况下，我们是完全错误的，我们的成本将是：

-log（0.05）= 2.996

这个成本要高得多。该模型非常确定我会错过，这是错误的，因此我们要严厉惩罚它。我们能够做到这一点归功于采用自然对数。

下面的图显示了成本与我们的预测之间的关系（第一个图显示了当实际结果= 1时成本相对于我们的预测如何变化，第二个图显示了当A 精算结果= 0时成本相对于我们的预测的变化）。

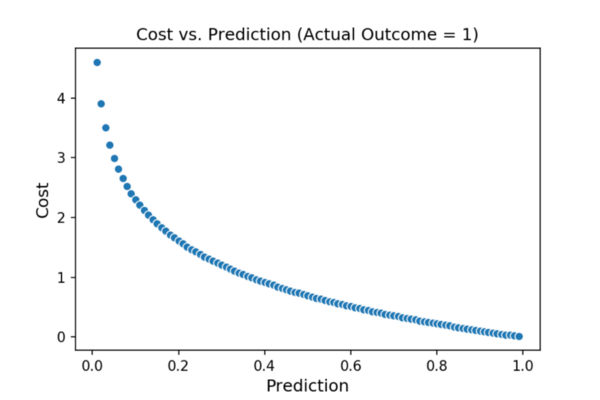
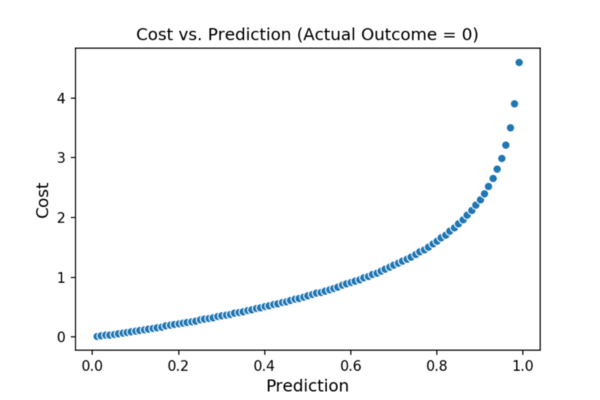
因此，对于给定的观察，我们可以将成本计算为：

如果实际结果= 1，则成本= -log（pred_prob）
否则 实际结果= 0， 然后 费用= -log（1-pred_prob）
其中pred_prob是从我们的模型中弹出的预测概率。

对于我们的整个数据集，我们可以通过以下方式计算总成本：
使用上述步骤计算每个观测值的个人成本。
将所有的个人成本加总即可得出总成本。
这个总成本是我们希望尽量减少数量，我们可以用这样做梯度下降优化。换句话说，我们可以进行优化以找到使总成本最小的B0和B1值。一旦找到了答案，便有了模型。令人兴奋！

+++绑在一起
综上所述，首先我们使用优化来搜索使成本函数最小的B0和B1的值。这为我们提供了模型：

Z = B0 + B1 * X
其中B0 = 2.5，B1 = -0.2（通过优化确定）

我们可以看一下斜率系数B1，它测量距离对我的拍摄精度的影响。我们估计B1为-0.2。这意味着，距离每增加1英尺，我投篮的对数几率降低0.2。y轴截距B0的值为2.5。这是当我从0英尺（紧靠篮筐）投篮时模型的对数赔率预测。通过sigmoid函数运行该函数可得出92.4％的预测概率。在下面的图中，绿点表示Z，即我们预测的对数几率。

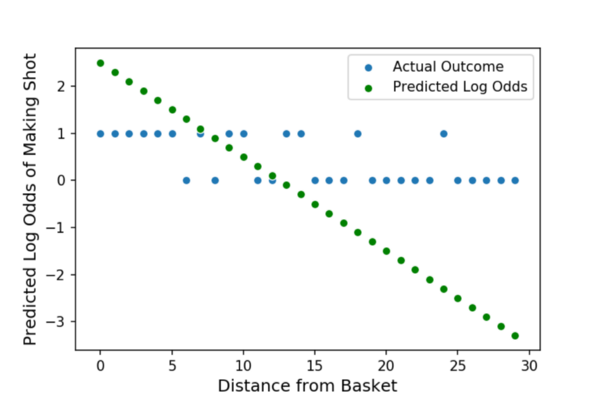
我们快完成了！由于Z处于对数赔率，因此我们需要使用S型函数将其转换为概率：

投篮的概率= 1 / [1 + e ^（-Z）]

下图中的橙色点表示了我们所追求的最终输出 “投篮”的概率。注意曲率。这意味着我的特征（距离）与目标之间的关系不是线性的。在概率空间（与对数赔率或线性回归不同），我们不能说我的投篮距离与我的投篮概率之间存在恒定的关系。相反，距离对概率的影响（连接橙色点的直线的斜率）本身就是我当前距离篮筐多远的函数。

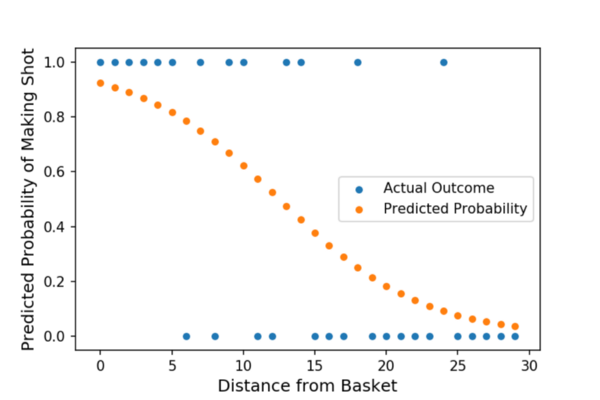
---希望这可以帮助您更好地了解逻辑回归（编写它绝对可以帮助我）。