JavaScript版数据结构与算法

JavaScript版数据结构与算法 轻松解决前端算法面试

'第1章 数据结构与算法简介/1-1 课程介绍_.mp4'

JavaScript版数据结构与算法轻松解决前端算法面试

掌握数据结构与算法的理论知识。补齐求职面试中的算法短板。梳理前端与算法结合点，不再纸上谈兵，将算法用于实战。

理论：数据结构与算法的特点、应用场景等等。刷题：做一些算法题，推荐使用LeetCode。实战：在工作中与数据结构/算法打交道。

数据结构栈队列集合链表字典树堆图

进阶算法冒泡算法选择算法插入算法归并算法快速算法顺序算法二分搜索

算法设计思想分而治之动态规划贪心回溯

重点关注：数据结构与算法的特点、应用场景、JS实现、时间/空间复杂度。

刷题刷题网站：推荐使用LeetCode。刷题顺序：推荐按照类型刷题，相当于集中训练。重点关注：通用套路、时间/空间复杂度分析和优化。

数据结构与算法是什么？数据结构：计算机存储、组织数据的方式，就像锅碗瓢盆。算法：一系列解决问题的清晰指令，就像食谱。

数据结构与算法的关系程序=数据结构+算法。数据结构为算法提供服务，算法围绕数据结构操作。

栈、队列、链表。集合、字典。树、堆、图。

链表：遍历链表、删除链表节点。树、图：深度/广度优先遍历。数组：冒泡/选择/插入/归并/快速排序、顺序/二分搜索。

LeetCode 是什么?LeetCode 是一个专注于程序员技术成长和企业技术人才服务的品牌。功能：题库、社区、竞赛、模拟面试等等。

如何在题库搜题？通过题号搜索。通过难度、状态、列表、标签搜索。通过企业搜索（需要付费）。

企业题库LeetCode

如何做题？查看题目描述、评论、题解、提交记录。

'第1章 数据结构与算法简介/1-2 数据结构与算法简介.mp4'
'第1章 数据结构与算法简介/1-3 如何刷 LeetCode？_.mp4'

'第2章 时间空间复杂度计算/2-1 时间复杂度计算_.mp4'

时间复杂度是什么？一个函数，用大O表示，比如O（1)、O（n)、O（(logN)..…定性描述该算法的运行时间

空间复杂度是什么？一个函数，用大O表示，比如O（1）、O（n）、O（nへ2）.……算法在运行过程中临时占用存储空间大小的量度

O(1) O(logn) O(n)  O(n*n) O(n* *n+)

'第2章 时间空间复杂度计算/2-2 空间复杂度计算_.mp4'

'第3章 数据结构之“栈”/3-1 栈简介_ (2).mp4'

栈是什么？一个后进先出的数据结构。JavaScript 中没有栈，但可以用Array 实现栈的所有功能。

需要后进先出的场景。比如：十进制转二进制、判断字符串的括号是否有效、函数调用堆栈….

场景三：函数调用堆栈

最后调用的函数，最先执行完。JS解释器使用栈来控制函数的调用顺序。

20. 有效的括号

/**
 * @param {string} s
 * @return {boolean}
 */
var isValid = function(s) {
    if(s.length%2===1)return false;
    let stack=[];
    for(let i=0;i<s.length;i++){
        let c=s[i]
        if(c==='('||c==='['||c==='{'){
            stack.push(c);
        }else{
            let t=stack[stack.length-1]
            if((t==='('&&c===')')||(t==='['&&c===']')||(t==='{'&&c==='}')){
                stack.pop()
            }else{
                return false;
            }
        }
    }
    return stack.length===0;
};

fun->fun->fun

栈是一个后进先出的数据结构。JavaScript 中没有栈，但可以用Array 实现栈的所有功能。栈常用操作：push、pop、stack[stack.length-1]

'第3章 数据结构之“栈”/3-2 什么场景下用栈_ (2).mp4'
'第3章 数据结构之“栈”/3-3 LeetCode：20.有效的括号_ (2).mp4'
'第3章 数据结构之“栈”/3-4 前端与栈：JS 中的函数调用堆栈_ (2).mp4'
'第3章 数据结构之“栈”/3-5 栈-章节总结_ (2).mp4'

'第4章 数据结构之“队列”/4-1 队列简介_.mp4'

一个先进先出的数据结构。JavaScript 中没有队列，但可以用Array实现队列的所有功能。

in push out shift

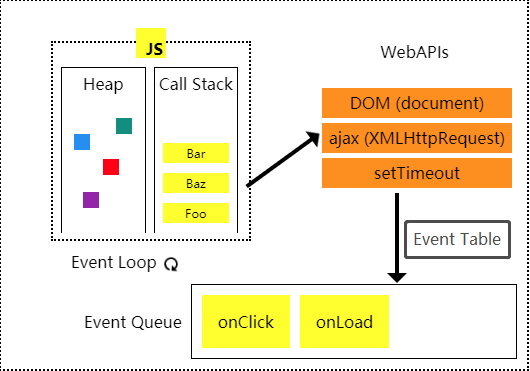
队列的应用场景需要先进先出的场景。比如：食堂排队打饭、JS异步中的任务队列、计算最近请求次数。

LeetCode：933.最近的请求次数

var RecentCounter = function() {
    this.queue=[]
};

/** 
 * @param {number} t
 * @return {number}
 */
RecentCounter.prototype.ping = function(t) {
    this.queue.push(t)
    while(this.queue[0]<t-3000){
        this.queue.shift()
    }
    return this.queue.length;
};

/** 
 * Your RecentCounter object will be instantiated and called as such:
 * var obj = new RecentCounter()
 * var param_1 = obj.ping(t)
 */

'第4章 数据结构之“队列”/4-2 什么场景用队列.mp4'
'第4章 数据结构之“队列”/4-3 LeetCode：933. 最近的请求次数_.mp4'
'第4章 数据结构之“队列”/4-4 前端与队列：JS 异步中的任务队列_.mp4'

'第4章 数据结构之“队列”/4-5 队列-章节总结_.mp4'

'第5章 数据结构之“链表”/5-1 链表简介_.mp4'

链表是什么？多个元素组成的列表。元素存储不连续，用next指针连在一起。

单 双 带头 不带头 loop链表

数组vs链表数组：增删非首尾元素时往往需要移动元素。链表：增删非首尾元素，不需要移动元素，只需要更改next的指向即可。

JavaScript 中没有链表。可以用Object模拟链表。

let a={val:1}
let b={val:2}
let c={val:3}
a.next=b
b.next=c

let p=a
while(p!=null){
    console.log(p.val)
    p=p.next
}

//add
let e={val:4}
c.next=e

//remove
a.next=c //remove b

237.删除链表中的节点

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} node
 * @return {void} Do not return anything, modify node in-place instead.
 */
var deleteNode = function(node) {
    node.val=node.next.val
    node.next=node.next.next
};

LeetCode:206.反转链表

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var reverseList = function(head) {
    let p1=head;
    let p2=null
    while(p1){
        let temp=p1.next
        p1.next=p2
        p2=p1
        p1=temp
    }
    return p2;
};

2.两数相加

class ListNode {
    constructor(val, next) {
        this.val = (val === undefined ? 0 : val)
        this.next = (next === undefined ? null : next)
    }
}
/**
 * @param {ListNode} l1
 * @param {ListNode} l2
 * @return {ListNode}
 */
var addTwoNumbers = function(l1, l2) {
    let p1=l1
    let p2=l2
    let arr=[]
    let carry=0 // 进位
    while(p1||p2){
        let current1=p1?p1.val:0
        let current2=p2?p2.val:0
        let sun=current1+current2+carry
        carry=Math.floor(sun/10)
        arr.push(sun%10)
        if(p1)p1=p1.next
        if(p2)p2=p2.next
    }
    if(carry)arr.push(carry)
    return buildLinkedList(arr)
};
// up time:6ms  space:56mb


// 4ms 56mb
var addTwoNumbersSimple = function(l1, l2) {
    let head = new ListNode(0)
    let p1=l1
    let p2=l2
    let p3=head
    let carry=0 // 进位
    while(p1||p2){
        let current1=p1?p1.val:0
        let current2=p2?p2.val:0
        let sun=current1+current2+carry
        carry=Math.floor(sun/10)
        p3.next=new ListNode(sun%10)
        if(p1)p1=p1.next
        if(p2)p2=p2.next
        p3=p3.next
    }
    // 处理最高位
    if(carry) p3.next=new ListNode(carry)
    return head.next
};

let a1 = [9,9,9,9,9,9,9], a2 = [9,9,9,9]
let l1= buildLinkedList(a1);
let l2= buildLinkedList(a2);
console.log(addTwoNumbers(l1, l2));

function buildLinkedList(arr) {
    let head = new ListNode(0);
    let p = head;
    for (let i = 0; i < arr.length; i++) {
        p.next = new ListNode(arr[i]);
        p = p.next;
    }
    return head.next;
}

to arr/reduce tolink

LeetCode：83.删除排序链表中的重复元素

class ListNode {
    constructor(val, next) {
        this.val = (val === undefined ? 0 : val)
        this.next = (next === undefined ? null : next)
    }
}
var deleteDuplicates = function(head) {
    let p=head
    //head have val next
    while(p&&p.next){
        if(p.val===p.next.val){
            p.next=p.next.next
        }else{
            p=p.next
        }
    }
    // p have next not val
    return head
};
let arr = [1,2,2,3,3]
let head=buildLinkedList(arr)
console.log(deleteDuplicates(head));

function buildLinkedList(arr) {
    let head = new ListNode(0);
    let p = head;
    for (let i = 0; i < arr.length; i++) {
        p.next = new ListNode(arr[i]);
        p = p.next;
    }
    return head.next;
}

LeetCode：141.环形链表

双指针 快+1=慢 true
class ListNode {
    constructor(val, next) {
        this.val = (val === undefined ? 0 : val)
        this.next = (next === undefined ? null : next)
    }
}
var hasCycle = function(head) {
    let fast=head
    let slow=head
    while(fast&&slow&&fast.next){
        if(fast.next===slow){
            return true
        }else{
            fast=fast.next.next
            slow=slow.next
        }
    }
    return false
};

let arr = [1,2]
let head=buildLinkedList(arr)
head.next = head;
console.log(hasCycle(head));

function buildLinkedList(arr) {
    let head = new ListNode(0);
    let p = head;
    for (let i = 0; i < arr.length; i++) {
        p.next = new ListNode(arr[i]);
        p = p.next;
    }
    return head.next;
}

前端与链表：JS中的原型链

原型链简介原型链的本质是链表。原型链上的节点是各种原型对象，比如Function.prototype、 Object.prototype.....原型链通过_proto_属性连接各种原型对象。

原型链长啥样？obj -> Object.prototype -> nullfunc -> Function.prototype -> Object.prototype ->nullarr -> Array.prototype -> Object.prototype -> null

前端与链表：使用链表指针获取JSON的节点值

数组和对象/json 组合找对象对应key

技术要点链表里的元素存储不是连续的，之间通过 next连接。JavaScript 中没有链表，但可以用Object模拟链表。链表常用操作：修改next、遍历链表。

'第5章 数据结构之“链表”/5-2 LeetCode：237.删除链表中的节点_.mp4'
'第5章 数据结构之“链表”/5-3 LeetCode：206.反转链表_.mp4'
'第5章 数据结构之“链表”/5-4 LeetCode：2. 两数相加_.mp4'
'第5章 数据结构之“链表”/5-5 LeetCode：83. 删除排序链表中的重复元素_.mp4'
'第5章 数据结构之“链表”/5-6 LeetCode：141. 环形链表_.mp4'
'第5章 数据结构之“链表”/5-7 前端与链表：JS 中的原型链_.mp4'
'第5章 数据结构之“链表”/5-8 前端与链表：使用链表指针获取 JSON 的节点值_.mp4'
'第5章 数据结构之“链表”/5-9 链表-章节总结_.mp4'
'第5章 数据结构之“链表”/本章精华部分.mp4'

'第6章 数据结构之“集合”/6-1 集合简介_ (2).mp4'

集合是什么？一种无序且唯一的数据结构。ES6中有集合，名为Set。集合的常用操作：去重、判断某元素是否在集合中、求交集

let arr=[1,2,2,4,5,6,7,8,9,10]
let unRepeat=[...new Set(arr)]
console.log(unRepeat)

let set1=new Set([1,2,3])
let set2=new Set([3,4,5])

console.log(set1)

//Intersection LeetCode：349.两个数组的交集
let intersection=new Set([...set1].filter(item=>set2.has(item)))
console.log(`intersection:`,union)
var intersection = function(nums1, nums2) {
    let set2=new Set(nums2);
    let set1=new Set(nums1)
   return [...set1].filter(item=>set2.has(item))
};


//union 
let arrset1=[...set1]
let arrset2=[...set2]
let left=arrset1.filter(item=>!arrset2.includes(item))
let right=arrset2.filter(item=>!arrset1.includes(item))
let union=new Set([...left,...right])
console.log(`union:`,intersection)


//差集
console.log('差集:',left,'or',right)

//补集∁UA
let diffsection=new Set([...set2].filter(item=>!set1.has(item)))
console.log(`set1补集:`,diffsection)

https://baijiahao.baidu.com/s?id=1757528805358274728&wfr=spider&for=pc
假设全集U={1，2，3，4，5，6}，集合A={1，3，5}，那么集合A在全集U中的补集就是由全集U中所有不属于A的元素组成的集合，即∁UA={2，4，6}。

使用Set对象：new、add、delete、has、size

weakset

迭代Set：多种迭代方法、Set与Array互转、求交集/差集

for of Array.from [....set1]

'第6章 数据结构之“集合”/6-2 LeetCode：349. 两个数组的交集_ (2).mp4'
'第6章 数据结构之“集合”/6-3 前端与集合：使用 ES6 中 Set_ (2).mp4'
'第6章 数据结构之“集合”/6-4 集合章节总结_ (2).mp4'

'第7章 数据结构之“字典”/7-1 字典简介_.mp4'

字典是什么？与集合类似，字典也是一种存储唯一值的数据结构，但它是以键值对的形式来存储。ES6中有字典，名为Map。字典的常用操作：键值对的增删改查。

Map weakMap

LeetCode：349.两个数组的交集

//map version
var intersection = function(nums1, nums2) {
   let map1=new Map()
   nums1.forEach(item=>map1.set(item,true))
   let result=[]
   nums2.forEach(item=>{
    if(map1.has(item)){
        result.push(item)
        map1.delete(item)
    }
   })
   return result
};

LeetCode：20.有效的括号

var isValid = function(s) {
    if(s.length%2===1)return false;
    let stack=[];
    let map=new Map()
    map.set('(',')')
    map.set('[',']')
    map.set('{','}')
    for(let i=0;i<s.length;i++){
        let c=s[i]
        if(map.has(c)){
            stack.push(c);
        }else{
            let t=stack[stack.length-1]
            if(map.get(t)===c){
                stack.pop()
            }else{
                return false;
            }
        }
    }
    return stack.length===0;
};

LeetCode:1.两数之和

新建一个字典作为婚姻介绍所。nums里的值，逐个来介绍所找对象，没有合适的就先登记着，有合适的就牵手成功。

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number[]}
 */
var twoSum = function(nums, target) {
    let map=new Map()
    let diff
    let result=[]
    nums.forEach((item,index)=>{
        diff=target-item
        if(map.has(diff)){
            result=[index,map.get(diff)]
        }else{
            map.set(item,index)
        }
    })
    return result
};
//time 6ms 54mb  O(n)
// es6 api time fast

//for time 72ms 35mb

LeetCode：3.无重复字符的最长子串

优化用kmp

解题步骤用双指针维护一个滑动窗囗，用来剪切子串。不断移动右指针，遇到重复字符，就把左指针移动到重复字符的下一位。过程中，记录所有窗口的长度，并返回最大值。

时间复杂度：O(n)空间复杂度：O(m)，m是字符串中不重复字符的个数

var lengthOfLongestSubstring = function(s) {
    let str = '';
    let longestStr = '';
    for (let i = 0; i < s.length; i++) {
        if (!str.includes(s[i])) {
            str += s[i];
        } else {
            // Check if the current substring is longer than the longest found so far
            if (str.length > longestStr.length) {
                longestStr = str;
            }
            // Find the position of the repeated character in the current substring
            const repeatIndex = str.indexOf(s[i]);
            // Start a new substring from the next character after the repeated one
            str = str.substring(repeatIndex + 1) + s[i];
        }
    }
    // Final check to update the longest substring if needed
    if (str.length > longestStr.length) {
        longestStr = str;
    }
    console.log(longestStr);
    return longestStr.length;
};
console.log(lengthOfLongestSubstring('pwfwkew'))
//只能用 string 和数组  time O(n*n)  space O(n)

//Map Solution time O(n)  space O(m)
var lengthOfLongestSubstring = function(s) {
    let oneNeedle=0
    let twoNeedle=0
    let map=new Map()
    for(let i=0;i<s.length;i++){
        if(map.has(s[i])&&map.get(s[i])>=oneNeedle){
            oneNeedle=map.get(s[i])+1
        }
        twoNeedle=Math.max(twoNeedle,i-oneNeedle+1)
        map.set(s[i],i)
    }
    return twoNeedle
};
console.log(lengthOfLongestSubstring('pwfwkew'))

flowchart TD A[开始] --> B{是否遍历结束} B -->|No| C[获取当前字符] C --> D{字符是否存在于 map 且位置 >= oneNeedle} D -->|Yes| E[更新 oneNeedle] D -->|No| F[跳过更新 oneNeedle] E --> G[更新最大长度] F --> G G --> H[更新 map] H --> B B -->|Yes| I[返回最大长度]

2h+ 3-5

LeetCode：76.最小覆盖子串

+helper divdsx cpv+lean+ ed jux dsks forget Analytics to myself

解题思路先找出所有的包含T的子串。找出长度最小那个子串，返回即可。

用双指针维护一个滑动窗口。移动右指针，找到包含T的子串，移动左指针，尽量减少包含T的子串的长度。

循环上述过程，找出包含T的最小子串。

pic emum cai /radom

时间复杂度：O(m+n)，m是t的长度，n是s的长度。空间复杂度：O(m)

/**
 * @param {string} s
 * @param {string} t
 * @return {string}
 */
var minWindow = function(s, t) {
    let left=0
    let right=0
    let map = new Map()
    for(let i=0;i<t.length;i++){
        map.set(t[i],map.has(t[i])?map.get(t[i])+1:1)
    }
    //根据 标志 判断 left right 移动的条件
    let flagSize=map.size
    let minStr=""
    let newStr=''
    while(right<s.length){
        if(map.has(s[right])){
            map.set(s[right],map.get(s[right])-1)
            if(map.get(s[right])===0) flagSize--;
        }
        while(flagSize===0){
            newStr=s.substring(left,right+1)
            if(!minStr||newStr.length<minStr.length) minStr=newStr
            if(map.has(s[left])){
                map.set(s[left],map.get(s[left])+1)
                if(map.get(s[left])===1) flagSize++;
            }
            left++
        }
       right++
    }
    return minStr
};

let s = "ADOBECODEBANC", t = "ABC"
console.log(minWindow(s, t))

tips api useable

与集合类似，字典也是一种存储唯一值的数据结构，但它是以键值对的形式来存储。ES6中有字典，名为Map。字典的常用操作：键值对的增删改查。

flowchart TD A[开始] --> B{右指针是否到达 s 的末尾} B -->|No| C{当前字符在 map 中} C -->|Yes| D[更新 map 并检查标志] D --> E{标志是否为 0} E -->|Yes| F[更新最小子串并移动左指针] F --> G{左指针字符在 map 中} G -->|Yes| H[更新 map 并检查标志] H --> I{标志是否为 0} I -->|No| J[继续移动左指针] J --> E I -->|Yes| K[结束内层循环] K --> L[右指针加一] L --> B B -->|Yes| M[返回最小子串]

'第7章 数据结构之“字典”/7-2 LeetCode：349. 两个数组的交集_.mp4'
'第7章 数据结构之“字典”/7-3 LeetCode：20.有效的括号_.mp4'
'第7章 数据结构之“字典”/7-4 LeetCode：1. 两数之和_.mp4'
'第7章 数据结构之“字典”/7-5 LeetCode：3. 无重复字符的最长子串_.mp4'
'第7章 数据结构之“字典”/7-6 LeetCode：76. 最小覆盖子串_.mp4'
'第7章 数据结构之“字典”/7-7 字典-章节总结_.mp4'

'第8章 数据结构之“树”/8-1 树简介_.mp4'

颗粒化 宏光 组合/change

3804+ 4000- 4kn minwhile

mw 4kgod 4k god think

4gt

9bx+11 draw runner

variable

树是什么？一种分层数据的抽象模型。前端工作中常见的树包括：DOM树、级联选择、树形控件……

树是什么？JS中没有树，但是可以用Object和Array构建树。树的常用操作：深度/广度优先遍历、先中后序遍历。

这个是二×树
class TreeNode {
    constructor(val, left = null, right = null) {
      this.val = val;
      this.left = left;
      this.right = right;
    }
  }
// 构建测试用例
// let arrRoot = [-10,9,20,null,null,15,7];
// let arrRoot = [1,2,3];
let arrRoot = [-3];
let root = buildTree(arrRoot);
function buildTree(arr) {
    if (arr.length === 0) return null;
    let root = new TreeNode(arr[0]);
    let queue = [root];
    for (let i = 1; i < arr.length; i++) {
        let node = queue.shift();
        if (i * 2 - 1 < arr.length) {
            node.left = new TreeNode(arr[i * 2 - 1]);
            queue.push(node.left);
        }
        if (i * 2 < arr.length) {
            node.right = new TreeNode(arr[i * 2]);
            queue.push(node.right);
        }
    }
    return root;
}
console.log(maxPathSum(root));

树的深度与广度优先遍历

深度优先遍历：尽可能深的搜索树的分支。广度优先遍历：先访问离根节点最近的节点。

广度优先遍历算法口诀新建一个队列，把根节点入队。把队头出队并访问。把队头的 children 挨个入队。重复第二、三步，直到队列为空。

var tree={
    val:1,
    children:[
        {
            val:2,
            children:[
                {
                    val:4,
                    children:[
                       
                    ]
                },
                {
                    val:5,
                    children:[
                       
                    ]
                }
            ]
        },
        {
            val:3,
            children:[
                {
                    val:6,
                    children:[
                       
                    ]
                }
            ]
        }
    ]
}

// dfs
let dfsArr=[]
function dfs(tree){
    // console.log(tree.val)
    dfsArr.push(tree.val)
    if(!tree)return
    if(tree.children.length>0){
        for(let i=0;i<tree.children.length;i++){
            dfs(tree.children[i])
        }
    }
}
dfs(tree)
console.log(dfsArr)


var tree2={
    val:1,
    children:[
        {
            val:2,
            children:[
                {
                    val:4,
                    children:[
                       
                    ]
                },
                {
                    val:5,
                    children:[
                       
                    ]
                }
            ]
        },
        {
            val:3,
            children:[
                {
                    val:6,
                    children:[
                       
                    ]
                }
            ]
        }
    ]
}
//bfs
let bfsArr=[]
function bfs(tree){
    if(!tree)return
    let queue=[tree]
    let alter
    while(queue.length>0){
        alter=queue.shift()
        bfsArr.push(alter.val)
        if(alter.children.length>0){
            for(let i=0;i<alter.children.length;i++){
                queue.push(alter.children[i])
            }
        }
    }
}
bfs(tree2)
console.log(bfsArr)

//only is tree

二叉树的先中后序遍历

二叉树是什么？树中每个节点最多只能有两个子节点。在JS中通常用Object来模拟二叉树。

中序遍历算法囗诀对根节点的左子树进行中序遍历。访问根节点。对根节点的右子树进行中序遍历。

• postorder是left-right-root，所以输出在curr往左走之前

• preorder是root-left-right，所以输出在curr往左走之前

• inorder是left-root-right,所以输出在curr往右走之前

• extends 不同的三个数字(零除外)有6种组合(如:1，2，3等)。

• 排列组合的计算公式是：排列数,从n个中取m个排一下,有n(n-1)(n-2)...(n-m+1)种,即n/(n-m)

  

从n个不同元素中，任取m(m≤n）个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合；从n个不同元素中取出m(m≤n）个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数。用符号 C(n,m) 表示。

组合总数（total number of combinations）是一个正整数，指从n个不同元素里每次取出0个，1个，2个，…，n个不同元素的所有组合数的总和，即

n元集合的组合总数是它的子集的个数。从n个不同元素中每次取出m个不同元素而形成的组合数 的性质是：

1、

2、

利用这两个性质，可化简组合数的计算及证明与组合数有关的问题。

解:C3=3!=3(3一1)(3一2)=3X2X1=6(种)

https://blog.csdn.net/i042416/article/details/130752385

let tree={
    val:1,
    left:{
        val:2,
        left:null,
        right:null,
    },
    right:{
        val:3,
        left:null,
        right:null,
    }
}
// function preOrder(root){
//     if(!root)return
//     console.log(root.val)
//     preOrder(root.left)
//     preOrder(root.right)
// }
// preOrder(tree)
// function inOrder(root){
//     if(!root)return
//     inOrder(root.left)
//     console.log(root.val)
//     inOrder(root.right)
// }
// inOrder(tree)
function postOrder(root){
    if(!root)return
    postOrder(root.left)
    postOrder(root.right)
    console.log(root.val)
}
postOrder(tree)

二叉树的先中后序遍历（非递归版）// queue stack

let tree={
    val:1,
    left:{
        val:2,
        left:null,
        right:null,
    },
    right:{
        val:3,
        left:null,
        right:null,
    }
}
// function preOrder(root){
//     if(!root)return
//     console.log(root.val)
//     preOrder(root.left)
//     preOrder(root.right)
// }
// preOrder(tree)
// function inOrder(root){
//     if(!root)return
//     inOrder(root.left)
//     console.log(root.val)
//     inOrder(root.right)
// }
// inOrder(tree)
// function postOrder(root){
//     if(!root)return
//     postOrder(root.left)
//     postOrder(root.right)
//     console.log(root.val)
// }
// postOrder(tree)

// 非递归
// function preOrder(root){
//     if(!root)return
//     let stack=[root]
//     while(stack.length>0){
//        let node=stack.pop()
//        console.log(node.val);
//        if(node.right)stack.push(node.right)
//        if(node.left)stack.push(node.left)
//     }
// }
// preOrder(tree)

// function inOrder(root){
//     if(!root)return
//     let stack=[]
//     let node=root
//     let n
//     while(stack.length||node){
//        while(node){
//            stack.push(node)
//            node=node.left
//        }
//        n=stack.pop()
//        console.log(n.val)
//        node=n.right
//     }
// }
// inOrder(tree)
function postOrder(root){
    if(!root)return
    let stack=[root]
    let outStack=[]
    let n
    while(stack.length){
        n=stack.pop()
        outStack.push(n)
        if(n.left)stack.push(n.left)
        if(n.right)stack.push(n.right)
    }
    while(outStack.length){
        console.log(outStack.pop().val)   
    }
}
postOrder(tree)

LeetCode:104.二叉树的最大深度

var maxDepth = function(root) {
    if(!root) return 0
    let result=0
    function dfs(node,deep){
        result=Math.max(result,deep)
        if(node.left)dfs(node.left,deep+1)
        if(node.right)dfs(node.right,deep+1)
    }
    dfs(root,1)
    return result
};

LeetCode:111.二叉树的最小深度

解题思路求最小深度，考虑使用广度优先遍历。在广度优先遍历过程中，遇到叶子节点，停止遍历，返回节点层级。

解题步骤广度优先遍历整棵树，并记录每个节点的层级。遇到叶子节点，返回节点层级，停止遍历。

//dfs
var minDepth = function(root) {
    if (!root) return 0;
    function dfs(node) {
        if (!node.left && !node.right) return 1; // 叶子节点，返回深度1
        let leftDepth = Infinity, rightDepth = Infinity;
        if (node.left) leftDepth = dfs(node.left);
        if (node.right) rightDepth = dfs(node.right);
        return Math.min(leftDepth, rightDepth) + 1;
    }
    return dfs(root);
};

//bfs [][]
var minDepth = function(root) {
    if (!root) return 0;
    let queue = [[root, 1]];
    while(queue.length) {
        let [n,length]=queue.shift();
        if(!n.left&&!n.right) return length;
        if(n.left){queue.push([n.left,length+1])}
        if(n.right){queue.push([n.right,length+1])}
    }
};
// time 2ms   space 83.99mb  O(n)

//bfs []+{}
var minDepth = function(root) {
    if (!root) return 0;
    let queue = [{n:root,length:1}];
    while(queue.length) {
        let {n,length}=queue.shift();
        if(!n.left&&!n.right) return length;
        if(n.left){queue.push({n:n.left,length:length+1})}
        if(n.right){queue.push({n:n.right,length:length+1})}
    }
};
// time 4ms   space 83.96mb  O(n)

// time 7ms space 85.56mb 
//Map+Symbol*3
var minDepth = function(root) {
    if (!root) return 0;
    let s=Symbol('root')
    let map=new Map()
    map.set(s,{n:root,length:1})
    let key
    let n,length
    while(map.size>0) {
        key=Array.from(map.keys())[0]
        n=map.get(key).n
        length=map.get(key).length
        map.delete(key);
        if(!n.left&&!n.right) return length;
        if(n.left){map.set(Symbol(),{n:n.left,length:length+1})}
        if(n.right){map.set(Symbol(),{n:n.right,length:length+1})}
    }
};

//time 10ms  space 83.66mb
//Map+Symbol*3+WeakMap
var minDepth = function(root) {
    if (!root) return 0;
    let s=Symbol('root')
    let map=new Map()
    let weakMap=new WeakMap()
    weakMap.set(s,{n:root,length:1})
    map.set(s,weakMap)
    let key
    let n,length
    while(map.size>0) {
        key=Array.from(map.keys())[0];
        n=map.get(key).get(key).n;
        length=map.get(key).get(key).length;
        map.delete(key);weakMap.delete(key);
        if(!n.left&&!n.right) return length;
        if(n.left){let l=Symbol();map.set(l,weakMap.set(l,{n:n.left,length:length+1}))}
        if(n.right){let r=Symbol();map.set(r,weakMap.set(r,{n:n.right,length:length+1}))}
    }
    map=null
    weakMap=null
};

//time 14ms  space 86mb
// dfs preorder
var minDepth = function(root) {
    if (!root) return 0;
    
    let minDepth = Infinity;
    
    function preorder(node, depth) {
        if (!node) return;
        
        // If it's a leaf node
        if (!node.left && !node.right) {
            minDepth = Math.min(minDepth, depth);
        }
        
        preorder(node.left, depth + 1);
        preorder(node.right, depth + 1);
    }
    
    preorder(root, 1);
    
    return minDepth;
};

//只用map 和 一个symbol 不通过....error simple---not pass
//可能只能3个symbol----/...不知哪位大神改下...
var minDepth = function(root) {
    if (!root) return 0;
    
    let s = Symbol('node');
    let map = new Map();
    map.set(s, { node: root, depth: 1 });
    
    while (map.size > 0) {
        let { node, depth } = map.get(s);
        map.delete(s);
        
        if (!node.left && !node.right) {
            return depth;
        }
        
        if (node.left) {
            map.set(s, { node: node.left, depth: depth + 1 });
        }
        
        if (node.right) {
            // If left child exists, we need to process it first
            if (!map.has(s)) {
                map.set(s, { node: node.right, depth: depth + 1 });
            }
        }
    }
};

6/3

x jux edx ksdsx

LeetCode：102.二叉树的层序遍历

解题思路层序遍历顺序就是广度优先遍历。不过在遍历时候需要记录当前节点所处的层级，方便将其添加到不同的数组中。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */

function TreeNode(val, left, right) {
    this.val = (val === undefined ? 0 : val);
    this.left = (left === undefined ? null : left);
    this.right = (right === undefined ? null : right);
}

function buildTree(preorder) {
    if (preorder.length === 0) return null;
    
    let root = new TreeNode(preorder[0]);
    let queue = [root];
    let i = 1;
    
    while (i < preorder.length) {
        let currentNode = queue.shift();
        
        if (preorder[i] !== null) {
            currentNode.left = new TreeNode(preorder[i]);
            queue.push(currentNode.left);
        }
        i++;
        
        if (i < preorder.length && preorder[i] !== null) {
            currentNode.right = new TreeNode(preorder[i]);
            queue.push(currentNode.right);
        }
        i++;
    }
    
    return root;
}

var levelOrder = function(root) {
    if(!root) return []
    let queue = [root];
    let len,n
    let result=[]
    while(queue.length) {
       len=queue.length
       result.push([])
        while(len--){
            n=queue.shift()
            result[result.length-1].push(n.val)
            if(n.left)queue.push(n.left)
            if(n.right)queue.push(n.right)
        }
    }
    return result
};

// 构建二叉树
let preorder = [3,9,20,null,null,15,7];
let root = buildTree(preorder);

console.log(levelOrder(root)); 

LeetCode:94.二叉树的中序遍历

var inorderTraversal = function(root) {
     if(!root)return [];
    let stack=[]
    let node=root
    let n
    let result=[]
    while(stack.length||node){
       while(node){
           stack.push(node)
           node=node.left
       }
       n=stack.pop()
       result.push(n.val)
       node=n.right
    }   
    return result
};

var inorderTraversal = function(root) {
    if(!root)return [];
    let reuslt=[]
    function inOrder(node){
        if(node.left) inOrder(node.left)
         reuslt.push(node.val)
        if(node.right) inOrder(node.right)
    }
    inOrder(root)
    return reuslt
};

LeetCode：112.路径总和

解题思路在深度优先遍历的过程中，记录当前路径的节点值的和。在叶子节点处，判断当前路径的节点值的和是否等于目标值。

解题步骤深度优先遍历二叉树，在叶子节点处，判断当前路径的节点值的和是否等于目标值，是就返回true。遍历结束，如果没有匹配，就返回false。

var hasPathSum = function(root, targetSum) {
    if(!root) return false;
    let result=false
    function dfs(node,preVal){
        if((!node.left&&!node.right)&&preVal===targetSum){
            result=true;
        }
        if(node.left)dfs(node.left,node.left.val+preVal)
        if(node.right)dfs(node.right,node.right.val+preVal)
    }
    dfs(root,root.val)
    return result
};

前端与树：遍历JSON的所有节点值

const json={
    a:{b:{c:1}},
    d:[1,2]
}

const dfs=(n,path)=>{
    console.log(n,path);
    Object.keys(n).forEach((key)=>{
        if(Array.isArray(n[key])){
            dfs(n[key],path.concat(key));
        }  
    })
}
dfs(json,[]);

前端与树：渲染Antd的树组件

codepen.io/liuyiqi/pen/QWjqeNO?editors=0010

第8章 数据结构之“树”/8-10 前端与树：遍历 JSON 的所有节点值_.mp4'
'第8章 数据结构之“树”/8-11 前端与树：渲染 Antd 中的树组件_.mp4'
'第8章 数据结构之“树”/8-12 树-章节总结_.mp4'
'第8章 数据结构之“树”/8-2 深度与广度优先遍历_.mp4'
'第8章 数据结构之“树”/8-3 二叉树的先中后序遍历_.mp4'
'第8章 数据结构之“树”/8-4 二叉树的先中后序遍历（非递归版）.mp4'
'第8章 数据结构之“树”/8-5 LeetCode：104. 二叉树的最大深度.mp4'
'第8章 数据结构之“树”/8-6 LeetCode：111. 二叉树的最小深度_.mp4'
'第8章 数据结构之“树”/8-7 LeetCode：102. 二叉树的层序遍历_.mp4'
'第8章 数据结构之“树”/8-8 LeetCode：94. 二叉树的中序遍历_.mp4'
'第8章 数据结构之“树”/8-9 LeetCode：112. 路径总和_.mp4'
'第9章 数据结构之“图”/9-1 图简介_ (2).mp4'

图是什么？图是网络结构的抽象模型，是一组由边连接的节点。图可以表示任何二元关系，比如道路、航班.….

JS中没有图，但是可以用Object和Array构建图。图的表示法：邻接矩阵、邻接表、关联矩阵.….…

深度优先遍历广度优先遍历

图的深度与广度优先遍历

深度优先遍历：尽可能深的搜索图的分支。广度优先遍历：先访问离根节点最近的节点。

深度优先遍历算法囗诀imooc访问根节点。对根节点的没访问过的相邻节点挨个进行深度优先遍历。

广度优先遍历算法囗诀新建一个队列，把根节点入队。把队头出队并访问。把队头的没访问过的相邻节点入队。

stack queue .....4d

广度优先遍历算法囗诀新建一个队列，把根节点入队。把队头出队并访问。把队头的没访问过的相邻节点入队。重复第二、三步，直到队列为空。

const graph={
    0:[1,2],
    1:[2],
    2:[0,3],
    3:[3],
}
// const visited=new Set();
// var dfs=(node=parseInt(Object.keys(graph)[0]))=>{
//     console.log(node);
//     visited.add(node);
//     graph[node].forEach(item => {
//         if(!visited.has(item)){
//             dfs(item);
//         }
//     });
// }
// dfs();

const visited=new Set();
var bfs=(start=parseInt(Object.keys(graph)[0]))=>{
    let queue=[start];
    while(queue.length){
        let n=queue.shift(); 
        visited.add(n);  
        graph[n].forEach(item => {
            if(!visited.has(item)){
                queue.push(item);
                visited.add(n);  
            }
        });
    }
    return [...visited];
}
console.log(bfs(2))

// const visited=new Set();

// var bfsInout=(start=parseInt(Object.keys(graph)[0]))=>{
//     visited.add(start); 
//     let queue=[start];
//     while(queue.length){
//         let n=queue.shift(); 
//         console.log(n);
//         graph[n].forEach(item => {
//             if(!visited.has(item)){
//                 queue.push(item);
//                 visited.add(item);  
//             }
//         });
//     }
// }
// bfsInout(2)

LeetCode:65.有效数字

解题步骤构建一个表示状态的图。遍历字符串，并沿着图走，如果到了某个节点无路可走就返false。遍历结束，如走到3/5/6,就返回true,否则返回false。

extend 2 8 10 16进制

/**
 * 检查一个字符串是否可以表示为一个有效的数字
 * @param {string} s - 待检查的字符串
 * @returns {boolean} - 如果字符串是有效的数字表示，则返回true；否则返回false
 */
var isNumber = function(s) {
    // 状态转换图，定义了字符串中每个字符类型在不同状态下如何转换状态
    const graph = {
        0: {'blank': 0, 'sign': 1, '.': 2, 'digit': 6},
        1: {'digit': 6, '.': 2},
        2: {'digit': 3},
        3: {'digit': 3, 'e': 4},
        4: {'digit': 5, 'sign': 7},
        5: {'digit': 5},
        6: {'digit': 6, '.': 3, 'e': 4},
        7: {'digit': 5}
    };
    
    // 初始化状态为0
    let state = 0;
    
    // 遍历字符串中的每个字符，去除首尾空格
    for (let c of s.trim()) {
        // 将字符分类为digit、blank、.、e、sign
        if (c >= '0' && c <= '9') {
            c = 'digit';
        } else if (c === ' ') {
            c = 'blank';
        } else if (c === '.') {
            c = '.';
        } else if (c === 'e' || c === 'E') {
            c = 'e';
        } else if (c === '+' || c === '-') {
            c = 'sign';
        }
        
        // 根据当前状态和字符类型转换到下一个状态
        state = graph[state][c];
        
        // 如果转换结果为undefined，说明字符串不是有效的数字表示
        if (state === undefined) {
            return false;
        }
    }
    
    // 如果最终状态是3、5或6，则字符串是有效的数字表示
    return state === 3 || state === 5 || state === 6;
};

// 示例：检查字符串"1E9"是否是有效的数字表示
console.log(isNumber("1E9"));

代码功能详细解释

这段 JavaScript 代码的功能是判断给定的字符串是否表示一个有效的数字。它使用有限状态机（FSM）来处理字符串中的每个字符，并根据预定义的状态转换规则进行状态切换。具体步骤如下：

1. 初始化状态机：

   • 定义了一个 graph 对象，表示不同状态之间的转换规则。
   • 每个状态对应一个对象，键为字符类型（如 digit, blank, sign, ., e），值为下一个状态。

2. 遍历字符串：

   • 使用 trim() 方法去除字符串两端的空白字符。
   • 遍历处理后的字符串，逐个字符进行分类和状态转换。

3. 字符分类：

   • 数字字符（0-9）：转换为 digit。
   • 空格字符（ ）：转换为 blank。
   • 小数点字符（.）：保持不变。
   • 指数字符（e 或 E）：转换为 e。
   • 符号字符（+ 或 -）：转换为 sign。

4. 状态转换：

   • 根据当前字符和当前状态，在 graph 中查找下一个状态。
   • 如果找不到对应的转换规则（即 state === undefined），则返回 false，表示字符串不是有效数字。

5. 最终状态检查：

   • 遍历结束后，检查最终状态是否为合法的终止状态（3, 5, 6）。只有当最终状态为这些状态之一时，才返回 true，否则返回 false。

控制流图（CFG）

flowchart TD A[开始] --> B{字符串为空？} B -->|Yes| E[返回 false] B -->|No| C[初始化状态为0] C --> D[去除空白字符] D --> F[遍历字符串] F --> G{字符类型是什么？} G -->|digit| H[转换为 digit] G -->|blank| I[转换为 blank] G -->|.| J[转换为 .] G -->|e 或 E| K[转换为 e] G -->|+ 或 -| L[转换为 sign] H --> M[查找下一个状态] I --> M J --> M K --> M L --> M M --> N{找到下一个状态？} N -->|No| O[返回 false] N -->|Yes| P[更新状态] P --> Q{遍历结束？} Q -->|No| F Q -->|Yes| R{最终状态合法？} R -->|No| S[返回 false] R -->|Yes| T[返回 true]

关键点说明

1. 状态机设计：

   • 状态机的核心是 graph 对象，它定义了从一个状态到另一个状态的转换规则。
   • 每个状态都有不同的字符类型可以触发状态转换，例如在状态 0 下遇到 digit 会转移到状态 6。

2. 字符分类逻辑：

   • 通过条件判断将字符分为五类：digit、blank、.、e 和 sign。
   • 这种分类简化了状态转换的复杂度，使得代码更加简洁易读。

3. 循环遍历与状态更新：

   • 使用 for...of 循环遍历字符串中的每个字符。
   • 在每次迭代中，根据当前字符和当前状态查找下一个状态，并更新状态变量 state。
   • 如果在任何时刻找不到合适的转换规则，则立即返回 false。

4. 最终状态检查：

   • 遍历结束后，检查最终状态是否为合法的终止状态（3, 5, 6）。
   • 只有当最终状态为这些状态之一时，才认为字符串是一个有效的数字，返回 true；否则返回 false。

示例解析

以 console.log(isNumber("1E9")) 为例：

1. 初始化状态为 0。
2. 去除空白字符后，字符串为 "1E9"。
3. 遍历第一个字符 '1'：
   • 类型为 digit，根据 graph 规则从状态 0 转移到状态 6。
4. 遍历第二个字符 'E'：
   • 类型为 e，根据 graph 规则从状态 6 转移到状态 4。
5. 遍历第三个字符 '9'：
   • 类型为 digit，根据 graph 规则从状态 4 转移到状态 5。
6. 遍历结束，最终状态为 5，属于合法的终止状态，因此返回 true。

希望这个详细的解释能够帮助你更好地理解这段代码的工作原理。

3h-

LeetCode:417.太平洋大西洋水流问题

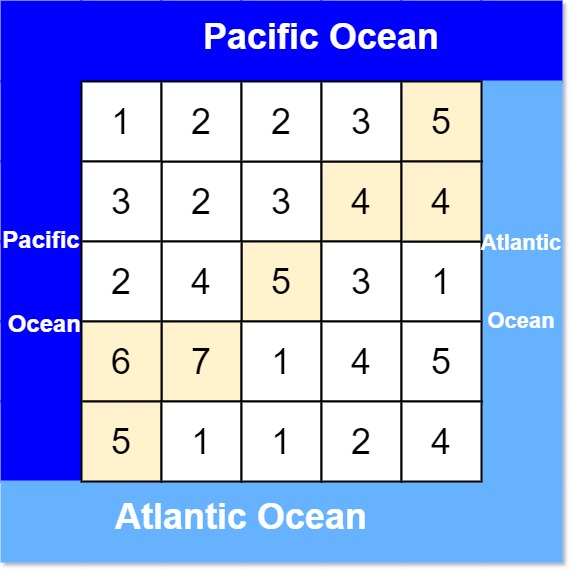
解题思路把矩阵想象成图。从海岸线逆流而上遍历图，所到之处就是可以流到某个大洋的坐标。

解题步骤新建两个矩阵，分别记录能流到两个大洋的坐标。从海岸线，多管齐下，同时深度优先遍历图，过程中填充上述矩阵。遍历两个矩阵，找出能流到两个大洋的坐标。

有一个 m × n 的矩形岛屿，与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。 这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。 岛上雨水较多，如果相邻单元格的高度 小于或等于 当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。 返回网格坐标 result 的 2D 列表 ，其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。

输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]] 输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]] 示例 2： 输入: heights = [[2,1],[1,2]] 输出: [[0,0],[0,1],[1,0],[1,1]]

	0
1		m
	n
	0
1		n
	m
	0n
1m		m
	n
	0m
1n		m
	n

//96ms 60.60mb
//81ms 60.59mb
//79ms 60.65mb
//57ms 60.65mb
//1stack bool null int +
/**
 * @param {number[][]} heights
 * @return {number[][]}
 */
var pacificAtlantic = function(heights) {
    let m=heights.length,n=heights[0].length;    // 获取矩阵的行数和列数
    let has=true
    let disHas=null
    let flow1=Array.from({length:m},()=>new Array(n).fill(disHas));   // 太平洋水流标记矩阵
    let flow2=Array.from({length:m},()=>new Array(n).fill(disHas)); 
    let result=[];
    var dfs=(x,y,flow)=>{
        flow[x][y]=has;    // 标记当前位置已经访问
        // 遍历四个方向||左||右||上||下
        [[x-1,y],[x+1,y],[x,y+1],[x,y-1]].forEach(([dx,dy])=>{    
            if(
                // 保证在矩阵中
                dx>=0&&dy>=0&&
                dx<m&&dy<n&&
                // 防止死循环
                !flow[dx][dy]&&
                // 保证水流方向是逆流
                heights[dx][dy]>=heights[x][y]    
            ){
                dfs(dx,dy,flow);    // 递归访问四个方向
            }
        })
    }
     // 遍历第一列和最后一列 //沿着海岸线逆流而上
    for(let i=0;i<m;i++){   
        dfs(i,0,flow1);    // 太平洋水流
        dfs(i,n-1,flow2);  // 大西洋水流
    }
    // 遍历第一行和最后一行
    for(let i=0;i<n;i++){   
        dfs(0,i,flow1); 
        dfs(m-1,i,flow2);  
    }
    for(let i=0;i<m;i++){
        for(let j=0;j<n;j++){
            if(flow1[i][j]&&flow2[i][j]){
                result.push([i,j]);
            }
        }
    }
    return result;
};
//39ms 60.48mb O(M*N)

LeetCode:133.克隆图

code lang change var / dissame lang change method ifame lang

解题思路拷贝所有节点。拷贝所有的边。

解题步骤深度或广度优先遍历所有节点。拷贝所有的节点，存储起来。将拷贝的节点，按照原图的连接方法进行连接。

var cloneGraph = function(node) {
    if(!node) return;
    let visited=new Map();
    var dfs=(root)=>{
        let init=new _Node(root.val);
        visited.set(root,init);
        (root.neighbors||[]).forEach(item=>{
            if(!visited.has(item)){
                dfs(item)
            }
            init.neighbors.push(visited.get(item))
        })
    }
    dfs(node);
    return visited.get(node)
};
//time:76ms/O(v+e) space:51.73mb/O(v)

//time:55ms/O(v+e) space:52.68mb/O(v)
var cloneGraph = function (node) {
    if (!node) return;
    let visited = new Map();
    let queue = [node];
    let n;
    visited.set(node, new _Node(node.val));
    while (queue.length) {
      n = queue.shift();
      (n.neighbors || []).forEach((item) => {
        if (!visited.has(item)) {
          queue.push(item);
          visited.set(item, new _Node(item.val));
        }
        visited.get(n).neighbors.push(visited.get(item));
      });
    }
    return visited.get(node);
  };

extend 带不带权图 出度 入度

图是网络结构的抽象模型，是一组由边连接的节点。图可以表示任何二元关系，比如道路、航班……。

JS中没有图，但是可以用Object和Array构建图。图的表示法：邻接矩阵、邻接表….图的常用操作：深度/广度优先遍历。

'第9章 数据结构之“图”/9-2 图的深度广度优先遍历_ (2).mp4'
'第9章 数据结构之“图”/9-3 LeetCode：65. 有效数字_ (2).mp4'
'第9章 数据结构之“图”/9-4 LeetCode：417. 太平洋大西洋水流问题_ (2).mp4'
'第9章 数据结构之“图”/9-5 LeetCode：133. 克隆图_ (2).mp4'
'第9章 数据结构之“图”/9-6 图-章节总结_ (2).mp4'

'第10章 数据结构之“堆”/10-1 堆简介_.mp4'

堆是什么？堆是一种特殊的完全二叉树。所有的节点都大于等于(最大堆）或小于等于（最小堆）它的子节点。

堆(完全二叉树)
	5
4		3
	3
4		5
JS中的堆JS中通常用数组表示堆。
左侧子节点的位置是2*index+1。
右侧子节点的位置是2*index+2。
父节点位置是(index-1)/2。跟不用
跟0 

堆的应用堆能高效、快速地找出最大值和最小值，时间复杂度：O(1)。找出第K个最大（小）元素。

扩展: 二叉搜索树/二叉平均数/黑红树...

第K个最大元素构建一个最小堆，并将元素依次插入堆中。当堆的容量超过K，就删除堆顶。插入结束后，堆顶就是第K个最大元素。

JavaScript 实现：最小堆类

在类里，声明一个数组，用来装元素。主要方法：插入、删除堆顶、获取堆顶、获取堆大小。

插入将值插入堆的底部，即数组的尾部。然后上移：将这个值和它的父节点进行交换，直到父节点小于等于这个插入的值。大小为k的堆中插入元素的时间复杂度为O（logk)。

---

https://www.runoob.com/w3cnote/bit-operation.html
https://oi-wiki.org/math/bit/
位运算 加快+-*/
2. 位运算概览
符号	描述	运算规则
&	与	两个位都为1时，结果才为1
|	或	两个位都为0时，结果才为0
^	异或	两个位相同为0，相异为1
~	取反	0变1，1变0
<<	左移	各二进位全部左移若干位，高位丢弃，低位补0
>>	右移	各二进位全部右移若干位，高位补0或符号位补齐
>>> 无符号右移
// 加法
console.log(9+21);
function add(x, y) {
    if (y == 0) return x;
    let sum = x ^ y; // 不带进位的加法
    let carry = (x & y) << 1; // 计算进位
    return add(sum, carry);
}
console.log(add(9, 21));



// 减法
console.log(4-2)
function subtract(x, y) {
    return add(x, ~y + 1);
}
console.log(subtract(4, 2));

// 乘法
console.log(4*2)
function multiply(x, y) {
    if (y === 0) return 0;
    let result = 0;
    while (y !== 0) {
        if (y & 1) result = add(result, x);
        x <<= 1;
        y >>>= 1;
    }
    return result;
}
console.log(multiply(4, 2));



// 除法
console.log(9/3)
function divide(dividend, divisor) {
    if (divisor === 0) throw new Error("Division by zero");
    if (dividend === 0) return 0;

    let isNegative = (dividend < 0) !== (divisor < 0);
    dividend = Math.abs(dividend);
    divisor = Math.abs(divisor);

    let quotient = 0;
    while (dividend >= divisor) {
        dividend = subtract(dividend, divisor);
        quotient = add(quotient, 1);
    }

    return isNegative ? negate(quotient) : quotient;
}
console.log(divide(9, 3));

//精度丢失问题 没解决 4ds jux
console.log(0.1+0.2)
console.log(add(0.1, 0.2));

删除堆顶用数组尾部元素替换堆顶（直接删除堆顶会破坏堆结构）。然后下移：将新堆顶和它的子节点进行交换，直到子节点大于等于这个新堆顶。大小为k的堆中删除堆顶的时间复杂度为O（logk)。

获取堆顶和堆的大小获取堆顶：返回数组的头部。获取堆的大小：返回数组的长度。

class MinHeap {
    constructor() {
      this.heap = []
      this.len = 0
    }
    size() {
      return this.len
    }
    push(val) {
      this.heap[++this.len] = val
      this.swin(this.len)
    }
  
    pop() {
      const ret = this.heap[1]
      this.swap(1, this.len--)
      this.heap[this.len + 1] = null
      this.sink(1)
      return ret
    }
    swin(ind) {
      while (ind > 1 && this.less(ind, parseInt(ind / 2))) {
        this.swap(ind, parseInt(ind / 2))
        ind = parseInt(ind / 2)
      }
    }
    sink(ind) {
      while (ind * 2 <= this.len) {
        let j = ind * 2
        if (j < this.len && this.less(j + 1, j)) j++
        if (this.less(ind, j)) break
        this.swap(ind, j)
        ind = j
      }
    }
    top() {
      return this.heap[1]
    }
    isEmpty() {
      return this.len === 0
    }
  
    swap(i, j) {
      [this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]]
    }
    less(i, j) {
      return this.heap[i] < this.heap[j]
    }
  }
  
class MinHeap{
    constructor(){
        this.heap = [];
    }
    getParentIndex(index){
        return (index-1)>>1; //等同于Math.floor((index-1)/2)
    }
    getLeftIndex(index){
        return 2*index+1;
    }
    getRightIndex(index){
        return 2*index+2; 
    }
    swap(i1,i2){
        let temp = this.heap[i1];
        this.heap[i1] = this.heap[i2];
        this.heap[i2] = temp;
    }
    shiftUp(index){
        if(index==0){return}
        let parentIndex=this.getParentIndex(index); //获取父节点的索引
        if(this.heap[parentIndex]>this.heap[index]){
            this.swap(parentIndex,index); //交换父节点和当前节点的值
            this.shiftUp(parentIndex)//继续向上调整，直到满足堆的性质为止
        }
    }
    shiftDown(index){
        let leftIndex=this.getLeftIndex(index); //获取左子节点的索引
        let rightIndex=this.getRightIndex(index); //获取右子节点的索引
        if(this.heap[leftIndex]<this.heap[index]){
            this.swap(leftIndex,index); 
            this.shiftDown(leftIndex) //继续向上调整，直到满足堆的性质为止
        }
        if(this.heap[rightIndex]<this.heap[index]){
            this.swap(rightIndex,index); 
            this.shiftDown(rightIndex) //继续向上调整，直到满足堆的性质为止
        }
    }
    insert(val){
        this.heap.push(val);
        this.shiftUp(this.heap.length - 1)
    }
    pop(){
        this.heap[0] = this.heap.pop();
        this.shiftDown(0);
    }
    peek(){
        return this.heap[0];
    }
    isEmpty(){
        return this.heap.length === 0;
    }
    size(){
        return this.heap.length;
    }
    getHeap(){
        return this.heap;
    }
    remove(val){
        for(let i=0;i<this.heap.length;i++){
            if(this.heap[i]===val) return this.heap.splice(i,1);
        }
    }
    max(k,arr){
       arr.forEach(n => {
        this.insert(n);
        if(this.size()>k){
            this.pop();
        }
       });
       return this.peek();
    }
    allInsert(arr){
        for(let i=0;i<arr.length;i++){
            this.insert(arr[i]);
        }
    }
}
let heap = new MinHeap();
// heap.insert(4);
// heap.insert(5);
// heap.insert(3);
// console.log(heap.getHeap()); // [3, 5, 4]
// // heap.remove(5);
// // console.log(heap.getHeap());
// heap.pop();
// console.log(heap.getHeap()); // [4,5]
// console.log(heap.peek()); // 4
// console.log(heap.size());
// console.log(heap.isEmpty());

//转完全二叉树 
function arrayToTree(arr) {
    if (!arr.length) return null;

    const root = { value: arr[0], left: null, right: null };
    const queue = [root];
    let i = 1;

    while (i < arr.length) {
        const current = queue.shift();

        if (i < arr.length) {
            current.left = { value: arr[i], left: null, right: null };
            queue.push(current.left);
            i++;
        }

        if (i < arr.length) {
            current.right = { value: arr[i], left: null, right: null };
            queue.push(current.right);
            i++;
        }
    }

    return root;
}

// const heapArray = heap.getHeap();
// const tree = arrayToTree(heapArray);
// console.log(tree);

LeetCode：215.数组中的第K个最大元素

解题思路看到“第K个最大元素”。考虑选择使用最小堆。

解题步骤构建一个最小堆，并依次把数组的值插入堆中。当堆的容量超过K，就删除堆顶。插入结束后，堆顶就是第K个最大元素。

leetcode在线 运行测试 可能是用本地环境跑分 ...有缓存 卡 大数有eroor

// 大数不通过 需要减少swap
class MinHeap{
    constructor(){
        this.heap = [];
    }
    getParentIndex(index){
        return (index-1)>>1; //等同于Math.floor((index-1)/2)
    }
    getLeftIndex(index){
        return 2*index+1;
    }
    getRightIndex(index){
        return 2*index+2; 
    }
    swap(i1,i2){
        let temp = this.heap[i1];
        this.heap[i1] = this.heap[i2];
        this.heap[i2] = temp;
    }
    shiftUp(index){
        if(index==0){return}
        let parentIndex=this.getParentIndex(index); //获取父节点的索引
        if(this.heap[parentIndex]>this.heap[index]){
            this.swap(parentIndex,index); //交换父节点和当前节点的值
            this.shiftUp(parentIndex)//继续向上调整，直到满足堆的性质为止
        }
    }
    shiftDown(index){
        let leftIndex=this.getLeftIndex(index); //获取左子节点的索引
        let rightIndex=this.getRightIndex(index); //获取右子节点的索引
        if(this.heap[leftIndex]<this.heap[index]){
            this.swap(leftIndex,index); 
            this.shiftDown(leftIndex) //继续向上调整，直到满足堆的性质为止
        }
        if(this.heap[rightIndex]<this.heap[index]){
            this.swap(rightIndex,index); 
            this.shiftDown(rightIndex) //继续向上调整，直到满足堆的性质为止
        }
    }
    insert(val){
        this.heap.push(val);
        this.shiftUp(this.heap.length - 1)
    }
    pop(){
        this.heap[0] = this.heap.pop();
        this.shiftDown(0);
    }
    peek(){
        return this.heap[0];
    }
    isEmpty(){
        return this.heap.length === 0;
    }
    size(){
        return this.heap.length;
    }
    getHeap(){
        return this.heap;
    }
    remove(val){
        for(let i=0;i<this.heap.length;i++){
            if(this.heap[i]===val) return this.heap.splice(i,1);
        }
    }
    max(k,arr){
       arr.forEach(n => {
        this.insert(n);
        if(this.size()>k){
            this.pop();
        }
       });
       return this.peek();
    }
    allInsert(arr){
        for(let i=0;i<arr.length;i++){
            this.insert(arr[i]);
        }
    }
}
//最快
var findKthLargest = function (nums, k) {
  nums = nums.sort((a, b) => b - a)
  return nums[k - 1]
};

var findKthLargest = function (nums, k) {
  for (let i = 0; i < k; i++) {
    for (let j = 0; j < nums.length - 1 - i; j++) {
      if (nums[j] > nums[j + 1])
        [nums[j], nums[j + 1]] = [nums[j + 1], nums[j]]
    }
  }
  return nums[nums.length - k]
};

var findKthLargest = function (nums, k) {
  let minHeap = new MinHeap()
  for (let i = 0; i < nums.length; i++) {
    if (minHeap.size() < k) minHeap.push(nums[i])
    else if (minHeap.top() < nums[i]) {
      minHeap.pop()
      minHeap.push(nums[i])
    }
  }
  return minHeap.top()
};

function binarySearch(arr, val) {
  let low = 0
  let high = arr.length - 1
  while (low <= high) {
    // mid 表示中间值
    let mid = Math.floor(low + (high - low) / 2)
    if (arr[mid] === val) return mid
    val < arr[mid] ? high = mid - 1 : low = mid + 1
  }
  return null
}

let arr = [0, 1, 2, 3, 4, 5]
console.log(binarySearch(arr, 0));

function quickSort(arr) {
  return quick(arr, 0, arr.length - 1)
}
function quick(arr, left, right) {
  if (arr.length > 1) {
    let index = partition(arr, left, right)
    if (left < index - 1) quick(arr, left, index - 1)
    if (index < right) quick(arr, index, right)
  }
  return arr
}

var findKthLargest = function (nums, k) {
  let low = 0
  let high = nums.length - 1
  while (low <= high) {
    const mid = partition(nums, low, high)
    if (mid === k - 1) return nums[mid]
    mid < k - 1 ? low = mid + 1 : high = mid - 1
  }

}

function partition(arr, low, high) {
  let mid = Math.floor(low + (high - low) / 2)
  const pivot = arr[mid]; // 这里记得添加分号 
  // 把pivot放在arr的最后面
  [arr[mid], arr[high]] = [arr[high], arr[mid]]
  let i = low
  // 把pivot排除在外,不对pivot进行排序
  let j = high - 1
  while (i <= j) {
    while (arr[i] > pivot) i++
    while (arr[j] < pivot) j--
    if (i <= j) {
      [arr[i], arr[j]] = [arr[j], arr[i]]
      i++; j--;
    }
  }
  // 因为arr[i]是属于left的,pivot也是属于left的
  // 故我们可以把原本保护起来的pivot和现在数组的中间值交换
  [arr[high], arr[i]] = [arr[i], arr[high]]
  return i
}
//https://juejin.cn/post/6844903913150218248

// 这个版本heap 可以
class MinHeap {
    constructor() {
      this.heap = []
      this.len = 0
    }
    size() {
      return this.len
    }
    push(val) {
      this.heap[++this.len] = val
      this.swin(this.len)
    }
  
    pop() {
      const ret = this.heap[1]
      this.swap(1, this.len--)
      this.heap[this.len + 1] = null
      this.sink(1)
      return ret
    }
    swin(ind) {
      while (ind > 1 && this.less(ind, parseInt(ind / 2))) {
        this.swap(ind, parseInt(ind / 2))
        ind = parseInt(ind / 2)
      }
    }
    sink(ind) {
      while (ind * 2 <= this.len) {
        let j = ind * 2
        if (j < this.len && this.less(j + 1, j)) j++
        if (this.less(ind, j)) break
        this.swap(ind, j)
        ind = j
      }
    }
    top() {
      return this.heap[1]
    }
    isEmpty() {
      return this.len === 0
    }
  
    swap(i, j) {
      [this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]]
    }
    less(i, j) {
      return this.heap[i] < this.heap[j]
    }
  }

LeetCode：347.前K个高频元素

var topKFrequent = function(nums, k) {
    let map=new Map();
    let arr=[...new Set(nums)]
    nums.forEach(item=>{
        if(map.has(item)){
            map.set(item,map.get(item)+1)
        }else{
            map.set(item,1)
        }
    })
    return arr.sort((a,b)=>map.get(b)-map.get(a)).slice(0,k)
};

class MinHeap {
    constructor() {
      this.heap = []
      this.len = 0
    }
    size() {
      return this.len
    }
    push(val) {
      this.heap[++this.len] = val
      this.swin(this.len)
    }
  
    pop() {
      const ret = this.heap[1]
      this.swap(1, this.len--)
      this.heap[this.len + 1] = null
      this.sink(1)
      return ret
    }
    swin(ind) {
      while (ind > 1 && this.less(ind, parseInt(ind / 2))) {
        this.swap(ind, parseInt(ind / 2))
        ind = parseInt(ind / 2)
      }
    }
    sink(ind) {
      while (ind * 2 <= this.len) {
        let j = ind * 2
        if (j < this.len && this.less(j + 1, j)) j++
        if (this.less(ind, j)) break
        this.swap(ind, j)
        ind = j
      }
    }
    top() {
      return this.heap[1]
    }
    isEmpty() {
      return this.len === 0
    }
  
    swap(i, j) {
      [this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]]
    }
    less(i, j) {
      return this.heap[i].val < this.heap[j].val
    }
    getHeap() {
      return this.heap
    }
  }
/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number[]}
 */
var topKFrequent = function(nums, k) {
    let map=new Map();
    nums.forEach(item=>{
        if(map.has(item)){
            map.set(item,map.get(item)+1)
        }else{
            map.set(item,1)
        }
    })
    let h=new MinHeap();
    map.forEach((val,key)=>{
        h.push({val,key});
        if(h.size()>k) h.pop();
    })
    return h.heap.filter(item=>item&&item.val).map(item=>item.key);
};

LeetCode:23.合并K个排序链表

解题思路新链表的下一个节点一定是k个链表头中的最小节点。考虑选择使用最小堆。

解题步骤构建一个最小堆，并依次把链表头插入堆中。弹出堆顶接到输出链表，并将堆顶所在链表的新链表头插入堆中。等堆元素全部弹出，合并工作就完成了。

class MinHeap {
    constructor() {
      this.heap = []
      this.len = 0
    }
    size() {
      return this.len
    }
    push(val) {
      this.heap[++this.len] = val
      this.swin(this.len)
    }
  
    pop() {
      if(this.top()===1) return this.heap.shift(1);
      const ret = this.heap[1]
      this.swap(1, this.len--)
      this.heap[this.len + 1] = null
      this.sink(1)
      return ret
    }
    swin(ind) {
      while (ind > 1 && this.less(ind, parseInt(ind / 2))) {
        this.swap(ind, parseInt(ind / 2))
        ind = parseInt(ind / 2)
      }
    }
    sink(ind) {
      while (ind * 2 <= this.len) {
        let j = ind * 2
        if (j < this.len && this.less(j + 1, j)) j++
        if (this.less(ind, j)) break
        this.swap(ind, j)
        ind = j
      }
    }
    top() {
      return this.heap[1]
    }
    isEmpty() {
      return this.len === 0
    }
  
    swap(i, j) {
      [this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]]
    }
    less(i, j) {
      return this.heap[i].val < this.heap[j].val
    }
    getHeap() {
      return this.heap
    }
  }
/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode[]} lists
 * @return {ListNode}
 */
var mergeKLists = function(lists) {
    if(!lists) return;
    let root=new ListNode(0);
    let h=new MinHeap()
    lists.forEach(n=>n&&h.push(n))
    let n;
    let p=root
    while(h.size()){
        n=h.pop();
        p.next=n
        p=p.next
        if(n.next)h.push(n.next)
    }
    return root.next
};

技术要点堆是一种特殊的完全二叉树。所有的节点都大于等于（最大堆）或小于等于（最小堆）它的子节点。JS中通常用数组表示堆。

技术要点堆能高效、快速地找出最大值和最小值，时间复杂度：O（1）。找出第K个最大（小）元素。

'第10章 数据结构之“堆”/10-2 JavaScript 实现：最小堆类_.mp4'
'第10章 数据结构之“堆”/10-3 LeetCode：215. 数组中的第 K 个最大元素_.mp4'
'第10章 数据结构之“堆”/10-4 LeetCode：347. 前 K 个高频元素_.mp4'
'第10章 数据结构之“堆”/10-5 LeetCode：23. 合并K个排序链表_.mp4'
'第10章 数据结构之“堆”/10-6 堆-章节总结_.mp4'

'第11章 进阶算法之“搜索排序”/11-1 排序和搜索简介.mp4'_

排序和搜索简介

排序和搜索是什么？排序：把某个乱序的数组变成升序或者降序的数组。搜索：找出数组中某个元素的下标。

JS 中的排序和搜索JS中的排序：数组的sort 方法。JS中的搜索：数组的indexOf方法。

排序算法归并排序冒泡排序选择排序快速排序插入排序

搜索算法顺序搜索二分搜索……………

https://www.xuhao.club/algo/algo-sort-search/

11-12【勤于思考，夯实学习成果】阶段思考题【勤于思考，夯实学习成果】阶段思考题
1、Chrome最新的Array.prototype.sort用的是什么排序算法?

V8 插入和快排

https://blog.csdn.net/weixin_43936704/article/details/104340019

2、用二分搜索算法求x的平方根。题目链接：https://leetcode-cn.com/problems/sqrtx/

ToDo69. x 的平方根

‌开平方根的方法主要有以下几种‌：

1. ‌分母有理化法‌：这种方法适用于处理无理数的平方根。具体步骤包括：

   • 设 $a = \sqrt{b}$，其中 $a$ 和 $b$ 均为非负实数。
   • 对 $a$ 进行分母有理化：$a = \frac{b-1}{b+1}$。
   • 解方程 $ax^2 + bx + c = 0$，求解得到 $x_1$ 和 $x_2$ 分别为 $a$ 和 $b$ 的平方根。‌

2. ‌牛顿迭代法‌：这是一种通过迭代逼近求解平方根的方法。步骤如下：

   • 设 $a$ 为要求平方根的数，初始值 $x_1 \approx \pm \sqrt{a}$。
   • 根据迭代公式 $x_{n+1} = x_n + \frac{a}{x_n}$，不断迭代直到满足一定的收敛条件。
   • 当 $|x_{n+1} - x_n| < \epsilon$（$\epsilon$ 为一个足够小的正数）时，认为找到了一个足够精确的平方根。

3. ‌二分法‌：通过不断缩小搜索范围来逼近平方根。步骤如下：

   • 设 $a$ 为要求平方根的数，取区间 $[0, \sqrt{a}]$ 作为搜索范围。
   • 取区间中点 $x = \frac{\sqrt{a} + 0}{2}$，计算 $f(x) = \frac{a}{x} - x^2$。
   • 根据 $f(x)$ 的正负性调整搜索范围，重复执行步骤，直到找到精确的平方根或达到预设的精度要求。

4. ‌笔算开平方法‌：适用于求任何正数的算术平方根。步骤包括：

   • 将被开方数的整数部分从个位起向左每隔两位划为一段，用撇号分开。
   • 根据左边第一段中的数，求得平方根的最高位上的数。
   • 从第一段的数中减去最高位上数的平方，形成第一个余数。
   • 用求得的最高位数乘以2试除第一个余数，得到的最大整数作为试商。
   • 用同样的方法继续求平方根的其他各位上的数。‌1

‌平方根的定义和性质‌：平方根表示为 $\pm \sqrt{a}$，其中非负数的平方根被称为算术平方根，表示为 $\sqrt{a}$。正数的平方根有两个值，互为相反数，负数没有平方根，0的平方根是0。‌2

/**
 * @param {number} x
 * @return {number}
 */
var mySqrt = function(x) {
    if (x < 0) {
        return -1;
    }
    if (x === 0 || x === 1) return x;
    let left = 0, right = x;
    while (left <= right) {
        let mid = Math.floor((left + right) / 2);
        if (mid * mid <= x && (mid + 1) * (mid + 1) > x) {
            return mid;
        } else if (mid * mid < x) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    // 出现意外行为时回退返回
    return left;
};

console.log(mySqrt(5));  // 输出应该是2

JavaScript 实现：冒泡排序

冒泡排序的思路比较所有相邻元素，如果第一个比第二个大，则交换它们。一轮下来，可以保证最后一个数是最大的。执行n-1轮，就可以完成排序。

冒泡排序的时间复杂度两个嵌套循环。时间复杂度：O(n^2)。

https://visualgo.net/zh/sorting

// JavaScript 实现：冒泡排序
Array.prototype.bubbleSort=function(){
    for(let i=0;i<this.length;i++){
        for(let j=0;j<this.length-i;j++){
            if(this[j]>this[j+1]){
                [this[j], this[j+1]] = [this[j+1], this[j]];
            }
        }
    }
    return this;
};

// 测试用例
var arr = [3, 1, 4,6, 2, 5]
console.log(arr.bubbleSort())

JavaScript 实现：选择排序

选择排序的时间复杂度两个嵌套循环。时间复杂度：0(n^2)。

//JavaScript 实现：选择排序
//select min to head two in head alter---same 
Array.prototype.selectSort=function(){
    let min=0;
    for(let i=0;i<this.length;i++){
        min=i;
        for(let j=i;j<this.length;j++){
            if(this[min]>this[j]){
                min=j;
            }
        }
        if(min!==i){
            [this[i], this[min]] = [this[min], this[i]];
        }
    }
    return this;
};

// 测试用例
var arr = [3, 1, 4, 6, 2, 5]
console.log(arr.selectSort())

JavaScript 实现：插入排序

插入排序的思路从第二个数开始往前比。比它大就往后排。以此类推进行到最后一个数。

插入排序的时间复杂度两个嵌套循环。时间复杂度：O(n^2)。

Array.prototype.insertSort=function(){
    let currentVal;
    let currentIndex;
    for(let i=1;i<this.length;i++){
        currentVal=this[i];
        currentIndex=i;
        for(currentIndex;currentIndex>0;currentIndex--){
            if(this[currentIndex-1]>currentVal){
                this[currentIndex]=this[currentIndex-1];
            }else{
                break;
            }
        }
        this[currentIndex]=currentVal;
    }
    return this;
};

// 测试用例
var arr = [3, 1, 4, 6, 2, 5]
console.log(arr.insertSort())

JavaScript 实现：归并排序

归并排序的思路分：把数组劈成两半，再递归地对子数组进行“分”操作，直到分成一个个单独的数。合：把两个数合并为有序数组，再对有序数组进行合并，直到全部子数组合并为一个完整数组。

合并两个有序数组新建一个空数组res，用于存放最终排序后的数组。比较两个有序数组的头部，较小者出队并推入res中。imooc如果两个数组还有值，就重复第二步。

归并排序的时间复杂度分的时间复杂度是O(logN)。合的时间复杂度是O(n)。时间复杂度：O(n*logN)。

归并 二分+ 猜

选择 贪心+ 猜

Array.prototype.mergeSort=function(){
    function merge(arr){
        if(arr.length===1) return arr;
        let mid=Math.floor(arr.length/2)
        let left=arr.slice(0,mid);
        let rgiht=arr.slice(mid,arr.length);
        let orderLeft=merge(left)
        let orderRight=merge(rgiht)
        let result=[]
        while(orderLeft.length || orderRight.length){
            if(orderLeft.length && orderRight.length){
                result.push(orderLeft[0] < orderRight[0] ? orderLeft.shift() : orderRight.shift())
            }
            else if(orderLeft.length) result.push(orderLeft.shift())
            else if(orderRight.length) result.push(orderRight.shift())
        }
        return result
    }
    merge(this).forEach((item,index)=>{this[index]=item});
    return this
};

// 测试用例
var arr = [3, 1, 4, 6, 2, 5]
console.log(arr.mergeSort())
console.log(arr)

JavaScript 实现：快速排序

快速排序的思路分区：从数组中任意选择一个“基准”，所有比基准小的元素放在基准前面，比基准大的元素放在基准的后面。递归：递归地对基准前后的子数组进行分区。

分组 min current max

快速排序的时间复杂度递归的时间复杂度是 O(logN)。分区操作的时间复杂度是O(n)。时间复杂度：O(n*logN)。

Array.prototype.quickSort=function(){
    const rec=(arr)=>{
        if(arr.length===1){return arr;};
        const left=[];
        const right=[];
        const mid=arr[0];
        for(let i=1;i<arr.length;i+=1){
            if(arr[i]<mid){
                left.push(arr[i])
            }
            else{right.push(arr[i])}
        }
        return [...rec(left),mid,...rec(right)]
    }
    rec(this).forEach((item,index)=>{this[index]=item});
    return this
};

// 测试用例
var arr = [3, 1, 4]
console.log(arr.quickSort())
//上面这个版本 new node 做了栈限制  多迭代 长数组 报错

Array.prototype.quickSort = function () {
    // 检查输入是否为数组
    if (!Array.isArray(this)) {
        throw new TypeError('Input must be an array');
    }

    const rec = (arr, left, right) => {
        if (left >= right) return;

        // 选择基准元素（使用三数取中法）
        const pivotIndex = Math.floor((left + right) / 2);
        [arr[left], arr[pivotIndex]] = [arr[pivotIndex], arr[left]];
        const pivot = arr[left];

        let i = left + 1;
        let j = right;

        while (i <= j) {
            while (i <= j && arr[i] < pivot) i++;
            while (i <= j && arr[j] > pivot) j--;
            if (i <= j) {
                [arr[i], arr[j]] = [arr[j], arr[i]];
                i++;
                j--;
            }
        }

        [arr[left], arr[j]] = [arr[j], arr[left]];

        rec(arr, left, j - 1);
        rec(arr, i, right);
    };

    rec(this, 0, this.length - 1);
    return this;
};

// 测试用例
var arr = [3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5]
console.log(arr.quickSort())

bubble=select=insert<quick<merge

JavaScript 实现：顺序搜索

顺序搜索的思路遍历数组。找到跟目标值相等的元素，就返回它的下标。遍历结束后，如果没有搜索到目标值，就返回-1。

顺序搜索的时间复杂度遍历数组是一个循环操作。时间复杂度：O(n)。

Array.prototype.sequantialSearch=function(key){
    for(let i=0;i<this.length;i++){
        if(this[i]===key) return i;
    }
    return -1;
}
console.log([1,2,3].sequantialSearch(2))

JavaScript 实现：二分搜索

二分搜索的思路从数组的中间元素开始，如果中间元素正好是目标值，则搜索结束。如果目标值大于或者小于中间元素，则在大于或小于中间元素的那一半数组中搜索。

二分搜索的时间复杂度每一次比较都使搜索范围缩小一半。时间复杂度：O(logN)。

Array.prototype.binarySearch=function(key){
    let low=0,high=this.length-1;
    while(low<=high){
        let mid=Math.floor((low+high)/2);
        let midVal=this[mid];
        if(midVal<key) low=mid+1;
        else if(midVal>key) high=mid-1;
        else return mid;
    }
    return -1;
}
console.log([1,2,3].binarySearch(2))
console.log([1,2,3].binarySearch(4))

LeetCode：21.合并两个有序链表

解题思路与归并排序中的合并两个有序数组很相似。将数组替换成链表就能解此题。

解题步骤新建一个新链表，作为返回结果。用指针遍历两个有序链表，并比较两个链表的当前节点，较小者先接入新链表，并将指针后移一步。链表遍历结束，返回新链表。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} list1
 * @param {ListNode} list2
 * @return {ListNode}
 */
var mergeTwoLists = function(list1, list2) {
    let root=new ListNode(0)
    let res=root
    let p1=list1;
    let p2=list2;
    while(p1&&p2){
        if(p1.val<p2.val){
            res.next=p1
            p1=p1.next
        }
        else{
            res.next=p2
            p2=p2.next
        }
        res=res.next
    }
    if(p1)res.next=p1;
    if(p2)res.next=p2;
    return root.next
};

LeetCode：374.猜数字大小

解题思路这不就是二分搜索嘛！调用guess函数，来判断中间元素是否是目标值。

解题步骤从数组的中间元素开始，如果中间元素正好是目标值，则搜索过程结束。如果目标值大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找。

/** 
 * Forward declaration of guess API.
 * @param {number} num   your guess
 * @return 	     -1 if num is higher than the picked number
 *			      1 if num is lower than the picked number
 *               otherwise return 0
 * var guess = function(num) {}
 */

/**
 * @param {number} n
 * @return {number}
 */
var guessNumber = function(n) {
    let low=0;
    let high=n
    while(low<=high){
        let mid=Math.floor((low+high)/2)
        let midVal=guess(mid)
        if(midVal===0){
            return mid
        }else if(midVal===1){
            low=mid+1
        }else{
            high=mid-1
        }
    }
    return -1
};

排序和搜索是什么？排序：把某个乱序的数组变成升序或者降序的数组。搜索：找出数组中某个元素的下标。

JS中的排序和搜索JS中的排序：数组的 sort方法。JS中的搜索：数组的 indexOf方法。

排序算法冒泡排序归并排序选择排序快速排序插入排序

搜索算法imooc顺序搜索二分搜索 kmp

ed

贪心 二分 折半 桶排sb… /组合4ds

堆排序、桶排序、计数排数

桶排序=二分分组

桶排序 safari brower sort

Array.prototype.mergeSort=function(){
    function merge(arr){
        if(arr.length===1) return arr;
        let mid=Math.floor(arr.length/2)
        let left=arr.slice(0,mid);
        let rgiht=arr.slice(mid,arr.length);
        let orderLeft=merge(left)
        let orderRight=merge(rgiht)
        let result=[]
        while(orderLeft.length || orderRight.length){
            if(orderLeft.length && orderRight.length){
                result.push(orderLeft[0] < orderRight[0] ? orderLeft.shift() : orderRight.shift())
            }
            else if(orderLeft.length) result.push(orderLeft.shift())
            else if(orderRight.length) result.push(orderRight.shift())
        }
        return result
    }
    merge(this).forEach((item,index)=>{this[index]=item});
    return this
};
function bucketSort(arr, bucketSize) {
    if (arr.length === 0) {
      return arr;
    }

    var i;
    var minValue = arr[0];
    var maxValue = arr[0];
    for (i = 1; i < arr.length; i++) {
      if (arr[i] < minValue) {
          minValue = arr[i];                // 输入数据的最小值
      } else if (arr[i] > maxValue) {
          maxValue = arr[i];                // 输入数据的最大值
      }
    }

    //桶的初始化
    var DEFAULT_BUCKET_SIZE = 5;            // 设置桶的默认数量为5
    bucketSize = bucketSize || DEFAULT_BUCKET_SIZE;
    var bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;   
    var buckets = new Array(bucketCount);
    for (i = 0; i < buckets.length; i++) {
        buckets[i] = [];
    }

    //利用映射函数将数据分配到各个桶中
    for (i = 0; i < arr.length; i++) {
        buckets[Math.floor((arr[i] - minValue) / bucketSize)].push(arr[i]);
    }

    arr.length = 0;
    for (i = 0; i < buckets.length; i++) {
        buckets[i].mergeSort()                  // 对每个桶进行排序，这里使用了插入排序
        for (var j = 0; j < buckets[i].length; j++) {
            arr.push(buckets[i][j]);                      
        }
    }

    return arr;
}
let arr=[5,3,2,4,1];
console.log(bucketSort(arr,5));

基数排序

Array.prototype.bubbleSort=function(){
    for(let i=0;i<this.length;i++){
        for(let j=0;j<this.length-i;j++){
            if(this[j]>this[j+1]){
                [this[j], this[j+1]] = [this[j+1], this[j]];
            }
        }
    }
    return this;
};
function bucketSort(arr, bucketSize) {
    if (arr.length === 0) {
      return arr;
    }

    var i;
    var minValue = arr[0];
    var maxValue = arr[0];
    for (i = 1; i < arr.length; i++) {
      if (arr[i] < minValue) {
          minValue = arr[i];                // 输入数据的最小值
      } else if (arr[i] > maxValue) {
          maxValue = arr[i];                // 输入数据的最大值
      }
    }

    //桶的初始化
    var DEFAULT_BUCKET_SIZE = 5;            // 设置桶的默认数量为5
    bucketSize = bucketSize || DEFAULT_BUCKET_SIZE;
    var bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;   
    var buckets = new Array(bucketCount);
    for (i = 0; i < buckets.length; i++) {
        buckets[i] = [];
    }

    //利用映射函数将数据分配到各个桶中
    for (i = 0; i < arr.length; i++) {
        buckets[Math.floor((arr[i] - minValue) / bucketSize)].push(arr[i]);
    }

    arr.length = 0;
    for (i = 0; i < buckets.length; i++) {
        buckets[i].bubbleSort()                  // 对每个桶进行排序，这里使用了插入排序
        for (var j = 0; j < buckets[i].length; j++) {
            arr.push(buckets[i][j]);                      
        }
    }

    return arr;
}
Array.prototype.radixSort=function(){
    let max = this[0];
    for (let i = 1; i < this.length; i++){
        if (this[i] > max)
            max = this[i];
    }
    // 从个位开始，对数组a按"指数"进行排序
    for (let exp = 1; max/exp > 0; exp *= 10){
        bucketSort(this, exp);
    }  
    return this;    
}

let arr=[222,334,8888,123,456]
console.log(arr.radixSort())
console.log(arr)

计数排序

算法的步骤如下： （1）找出待排序的数组中最大和最小的元素 （2）统计数组中每个值为i的元素出现的次数，存入数组C的第i项 （3）对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加） （4）反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1

function countingSort(arr, maxValue=0) {
    var bucket = new Array(maxValue+1),
        sortedIndex = 0;
        arrLen = arr.length,
        bucketLen = maxValue + 1;

    for (var i = 0; i < arrLen; i++) {
        if (!bucket[arr[i]]) {
            bucket[arr[i]] = 0;
        }
        bucket[arr[i]]++;
    }

    for (var j = 0; j < bucketLen; j++) {
        while(bucket[j] > 0) {
            arr[sortedIndex++] = j;
            bucket[j]--;
        }
    }

    return arr;
}
let arr= [1, 4, 1, 2, 7, 5, 2];
console.log(countingSort(arr, 7));

Shell排序/希尔排序

针对直接插入排序算法的改进

实质上是一种分组插入方法 分组—

function insertionSortWithGap(arr, length, startIndex, gap) {
    for (let j = startIndex + gap; j < length; j += gap) {
        let tmp = arr[j];
        let k = j - gap;
        // 确保 k + gap 不超过数组长度
        while (k >= 0 && k + gap < length && arr[k] > tmp) {
            arr[k + gap] = arr[k];
            k -= gap;
        }
        if (k + gap < length) {
            arr[k + gap] = tmp;
        } else {
            arr[length - 1] = tmp;
        }
    }
}

Array.prototype.shellSort = function() {
    let n = this.length;
    // gap为步长，每次减为原来的一半，并确保为整数
    for (let gap = Math.floor(n / 2); gap > 0; gap = Math.floor(gap / 2)) {
        // 共gap个组，对每一组都执行直接插入排序
        for (let i = 0; i < gap; i++) {
            insertionSortWithGap(this, n, i, gap);
        }
    }
    return this; // 返回排序后的数组
}

let arr = [222, 334, 8888, 123, 456];
arr.shellSort();
console.log(arr);

堆排序(Heap Sort)

堆排序是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

export {}
class HeapSort {
    // (最大)堆的向下调整算法
    public static maxHeapDown<T>(a: T[], start: number, end: number, compareFn: (a: T, b: T) => boolean) {
        let c = start;            // 当前(current)节点的位置
        let l = 2 * c + 1;        // 左(left)孩子的位置
        let tmp = a[c];           // 当前(current)节点的大小

        for (; l <= end; c = l, l = 2 * l + 1) {
            if (l + 1 <= end && compareFn(a[l], a[l + 1])) {
                l++;              // 左右两孩子中选择较大者
            }
            if (!compareFn(tmp, a[l])) {
                break;            // 调整结束
            } else {              // 交换值
                a[c] = a[l];
                a[l] = tmp;
            }
        }
    }

    // 堆排序(从小到大)
    public static heapSortAsc(a: number[], n: number) {
        if (n <= 0 || !a) return;

        console.log("Starting heapSortAsc with array:", a);

        const mid = Math.floor(n / 2 - 1);

        // 构建最大堆
        for (let i = mid; i >= 0; i--) {
            this.maxHeapDown(a, i, n - 1, (a, b) => a < b);
        }

        // 排序
        for (let i = n - 1; i > 0; i--) {
            [a[0], a[i]] = [a[i], a[0]]; // 交换a[0]和a[i]
            this.maxHeapDown(a, 0, i - 1, (a, b) => a < b);
        }

        console.log("Finished heapSortAsc with sorted array:", a);
    }

    // (最小)堆的向下调整算法
    public static minHeapDown<T>(a: T[], start: number, end: number, compareFn: (a: T, b: T) => boolean) {
        let c = start;            // 当前(current)节点的位置
        let l = 2 * c + 1;        // 左(left)孩子的位置
        let tmp = a[c];           // 当前(current)节点的大小

        for (; l <= end; c = l, l = 2 * l + 1) {
            if (l + 1 <= end && compareFn(a[l + 1], a[l])) {
                l++;              // 左右两孩子中选择较小者
            }
            if (!compareFn(a[l], tmp)) {
                break;            // 调整结束
            } else {              // 交换值
                a[c] = a[l];
                a[l] = tmp;
            }
        }
    }

    // 堆排序(从大到小)
    public static heapSortDesc(a: number[], n: number) {
        if (n <= 0 || !a) return;

        console.log("Starting heapSortDesc with array:", a);

        const mid = Math.floor(n / 2 - 1);

        // 构建最小堆
        for (let i = mid; i >= 0; i--) {
            this.minHeapDown(a, i, n - 1, (a, b) => a > b);
        }

        // 排序
        for (let i = n - 1; i > 0; i--) {
            [a[0], a[i]] = [a[i], a[0]]; // 交换a[0]和a[i]
            this.minHeapDown(a, 0, i - 1, (a, b) => a > b);
        }

        console.log("Finished heapSortDesc with sorted array:", a);
    }
}

// 使用不同的变量名来避免冲突
let originalArray = [1, 4, 1, 2, 7, 5, 2];
console.log("Original array:", originalArray);

// 执行堆排序并打印结果
HeapSort.heapSortAsc(originalArray, originalArray.length);
console.log("Sorted array:", originalArray);

不同的排序算法适用于不同的应用场景，选择合适的排序算法可以显著提高程序的效率。以下是根据各种排序算法的特点和优势所对应的应用场景：

1. 快速排序 (Quick Sort):

   • 适合于大多数通用排序任务，特别是当数据量较大时。
   • 在实践中是内部排序（即所有数据都存放在内存中）最常用的算法之一。

2. 归并排序 (Merge Sort):

   • 适合需要稳定排序的情况，例如在数据库管理系统中对记录进行排序。
   • 适用于外部排序（如磁盘上的大文件），因为它可以通过合并较小的有序块来处理大数据集。

3. 堆排序 (Heap Sort):

   • 当空间复杂度是一个重要考量因素时使用，因为它只需要O(1)的额外空间。
   • 适合实时系统或嵌入式系统等资源受限环境。

4. Shel排序 (Shell Sort):

   • 对于中等规模的数据集，尤其是当数据接近有序时，Shel排序可以提供较好的性能。
   • 它是一种插入排序的改进版本，因此也适用于在线排序（数据逐个到达）。

5. 插入排序 (Insertion Sort):

   • 非常适合小规模的数据集或者几乎已经排好序的数据。
   • 由于其简单性和低开销，它经常用于其他更复杂排序算法中的子程序。

6. 选择排序 (Selection Sort):

   • 主要用于教学目的，因为它的实现简单。
   • 实际应用较少，但对于非常小的数据集可能仍然适用。

7. 冒泡排序 (Bubble Sort):

   • 主要用于教学示例，展示基本排序概念。
   • 在实际生产环境中很少使用，因为它效率较低。

8. 桶排序 (Bucket Sort):

   • 当输入数据均匀分布在一定范围内时，桶排序能提供线性时间复杂度。
   • 适用于浮点数排序、IP地址排序等场景。

9. 基数排序 (Radix Sort):

   • 适用于整数排序，并且当数值范围较小时特别有效。
   • 例如，在电话号码排序或邮政编码排序等场景下表现良好。

10. 计数排序 (Counting Sort):

    • 适用于整数排序，特别是在已知整数范围有限的情况下。
    • 常见于统计分析或作为基数排序的一部分。

每个排序算法都有其特点和局限性，选择最适合特定问题的算法取决于具体的应用需求、数据特性和性能要求。

比稳定:

排序算法的性能通常依据时间复杂度和空间复杂度来评估。这里列出的排序算法按照一般情况下（平均时间复杂度）的性能从好到差进行排列。请注意，不同的场景和数据分布可能会影响这些排序算法的实际表现。

1. 快速排序 (Quick Sort) - 平均时间复杂度为 O(n log n)，最坏情况为 O(n^2)，但通过好的枢轴选择可以很大程度上避免最坏情况。空间复杂度为 O(log n)。
2. 归并排序 (Merge Sort) - 时间复杂度稳定在 O(n log n)，空间复杂度为 O(n)，因为它需要额外的空间来合并两个有序数组。
3. 堆排序 (Heap Sort) - 时间复杂度为 O(n log n)，空间复杂度为 O(1)，因为它是原地排序。
4. Shel排序 (Shell Sort) - 时间复杂度取决于增量序列的选择，最好情况为 O(n log n)，最坏情况接近 O(n^2)，空间复杂度为 O(1)。
5. 插入排序 (Insertion Sort) - 对于小规模或几乎已排序的数据集效果很好，时间复杂度为 O(n^2)，空间复杂度为 O(1)。
6. 选择排序 (Selection Sort) - 时间复杂度为 O(n^2)，空间复杂度为 O(1)，对于小规模数据集还可以接受。
7. 冒泡排序 (Bubble Sort) - 时间复杂度为 O(n^2)，空间复杂度为 O(1)，但在实际应用中很少使用，因为它效率较低。
8. 桶排序 (Bucket Sort) - 在特定条件下（如均匀分布的数据）可以达到 O(n)，但最坏情况下为 O(n^2)，并且空间复杂度较高。
9. 基数排序 (Radix Sort) - 对于固定长度的整数排序非常有效，时间复杂度为 O(n*k)，其中 k 是数字的位数，空间复杂度为 O(n + k)。
10. 计数排序 (Counting Sort) - 适用于范围有限的整数排序，时间复杂度为 O(n + k)，空间复杂度为 O(k)，其中 k 是输入数据的最大值。

请注意，这个列表中的排序并不是严格按性能好坏排序，因为不同算法在不同条件下的表现会有所不同。例如，基数排序和桶排序在某些特定条件下可以比其他算法更高效，而快速排序在实践中通常是最快的通用排序算法之一。此外，稳定性也是一个考虑因素，比如归并排序是稳定的，而快速排序不是。

'第11章 进阶算法之“搜索排序”/11-10 LeetCode：374. 猜数字大小_慕课网 2020-07-18 22_04.mp4'
'第11章 进阶算法之“搜索排序”/11-11 排序与搜索-章节总结_慕课网 2020-07-18 22_07.mp4'
'第11章 进阶算法之“搜索排序”/11-12 思考题.png'
'第11章 进阶算法之“搜索排序”/11-2 JavaScript 实现：冒泡排序.mp4'
'第11章 进阶算法之“搜索排序”/11-3 JavaScript 实现：选择排序.mp4'
'第11章 进阶算法之“搜索排序”/11-4 JavaScript 实现：插入排序.mp4'
'第11章 进阶算法之“搜索排序”/11-5 JavaScript 实现：归并排序.mp4'
'第11章 进阶算法之“搜索排序”/11-6 JavaScript 实现：快速排序.mp4'
'第11章 进阶算法之“搜索排序”/11-7 JavaScript 实现：顺序搜索.mp4'
'第11章 进阶算法之“搜索排序”/11-8 JavaScript 实现：二分搜索.mp4'
'第11章 进阶算法之“搜索排序”/11-9 LeetCode：21. 合并两个有序链表.mp4'

'第12章 算法设计思想之“分而治之”/12-1 分而治之简介.mp4'

分而治之是什么？分而治之是算法设计中的一种方法。它将一个问题分成多个和原问题相似的小问题，递归解决小问题，再将结果合并以解决原来的问题。

场景一：归并排序分：把数组从中间一分为二。解：递归地对两个子数组进行归并排序。合：合并有序子数组。

场景二：快速排序分：选基准，按基准把数组分成两个子数组。解：递归地对两个子数组进行快速排序。合：对两个子数组进行合并。

1n1 algorithm(狗去绿她们)/算法设计思想

五大基础算法（枚举、递归、分治、贪心、模拟）

1、说出分而治之算法的套路步骤。

分治算法的适用条件 分治算法能够解决的问题，一般需要满足以下 $4$ 个条件： 原问题可以分解为若干个规模较小的相同子问题。 分解出来的子问题可以独立求解，即子问题之间不包含公共的子子问题。 具有分解的终止条件，也就是说当问题的规模足够小时，能够用较简单的方法解决。 子问题的解可以合并为原问题的解，并且合并操作的复杂度不能太高，否则就无法起到减少算法总体复杂度的效果了。

分治算法的基本步骤 使用分治算法解决问题主要分为 $3$ 个步骤：

1.分解：把要解决的问题分解为成若干个规模较小、相对独立、与原问题形式相同的子问题。

2 求解：递归求解各个子问题。

3.合并：按照原问题的要求，将子问题的解逐层合并构成原问题的解。

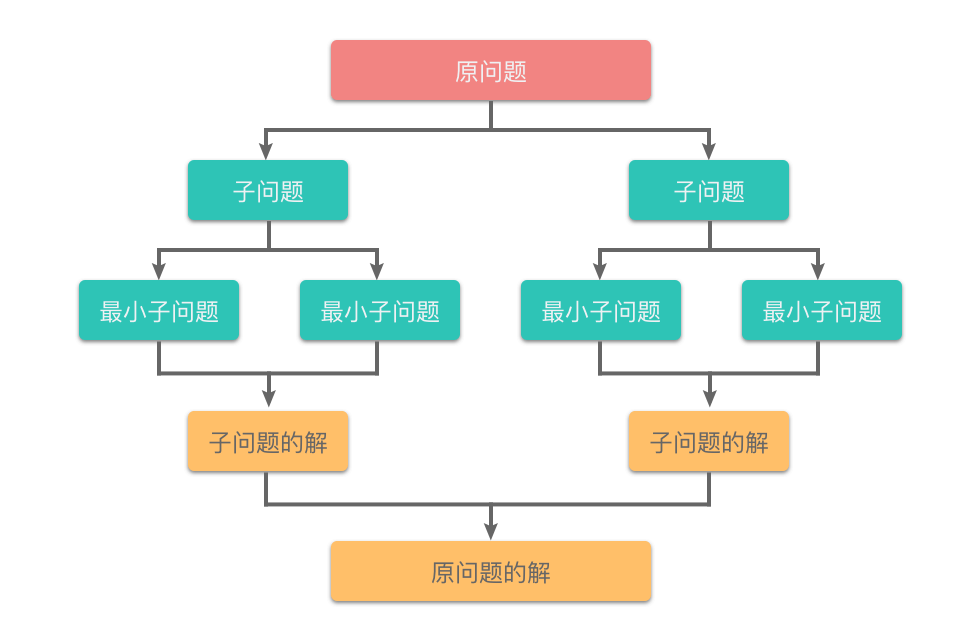
2、用分而治之的套路步骤，描述切西瓜的过程，无需Coding。

几刀问题 分块

分而治之（Divide and Conquer）是一种解决问题的策略，它将一个复杂的问题分解为若干个较小的子问题，分别解决这些子问题，然后将子问题的解组合起来得到原问题的解。下面是用分而治之的套路步骤来描述切西瓜的过程：

1. 问题划分：

   • 将整个西瓜看作是一个大问题。
   • 第一步是将西瓜从中间切成两半。这样就把一个大的西瓜切割问题转换成了两个较小的西瓜半边切割问题。

2. 递归处理：

   • 对每一个西瓜半边再次应用同样的方法：将每个半边再从中线切成两个更小的部分，即四分之一的西瓜。
   • 如果西瓜足够大或者需要更多的块数，继续对每个四分之一的西瓜重复上述步骤，直到达到所需的西瓜块大小或数量。

3. 基准情形（Base Case）：

   • 定义一个不再需要进一步切割的标准，例如当西瓜块达到了适合食用的大小时，停止切割。
   • 或者当西瓜已经被分割成预定的总块数时，也停止切割。

4. 合并解决方案：

   • 在分而治之的上下文中，合并通常意味着将所有子问题的解重新组合以形成原问题的完整解。
   • 在切西瓜的情况下，这个步骤并不是物理上的合并，而是指所有的西瓜块已经准备好可以被分配给不同的人享用。

5. 优化与调整：

   • 根据个人喜好调整切割方式，比如有些人可能喜欢圆形的片状西瓜，而有些人则偏好三角形的楔形块。
   • 考虑到皮和籽的位置，也可以调整切割的方向和位置，使得每一块都尽量没有白皮且籽最少。

通过以上步骤，我们使用了分而治之的方法成功地将一个完整的西瓜切割成了多个适于食用的小块。

LeetCode:374.猜数字大小

解题思路二分搜索，同样具备“分、解、合”的特性。考虑选择分而治之。

LeetCode:226.翻转二叉树

解题思路先翻转左右子树，再将子树换个位置。符合“分、解、合”特性。考虑选择分而治之。

解题步骤分：获取左右子树。解：递归地翻转左右子树。合：将翻转后的左右子树换个位置放到根节点上。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var invertTree = function(root) {
    if(!root)return null;
    return new TreeNode(root.val,invertTree(root.right),invertTree(root.left),)
};

LeetCode:100.相同的树

两个树：根节点的值相同，左子树相同，右子树相同。符合“分、解、合”特性。考虑选择分而治之。

分：获取两个树的左子树和右子树。解：递归地判断两个树的左子树是否相同，右子树是否相同。合：将上述结果合并，如果根节点的值也相同，树就相同。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {boolean}
 */
var isSameTree = function(p, q) {
    if(p===null&&q!==null){
        return false
    }
    if(p!==null&&q===null){
        return false
    }
    if(p===null&&q===null){
        return true
    }else{
        return p.val===q.val&&isSameTree(p.left,q.left) && isSameTree(p.right,q.right)
    }
    return isSameTree(p,q)
};
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {boolean}
 */
var isSameTree = function(p, q) {
    if(!p&&!q)return true;
    if(p&&q&&q.val===p.val&&isSameTree(p.left,q.left)&&isSameTree(p.right,q.right)){
     return true;
    }
    return false;
 };

LeetCode：101.对称二叉树

解题思路转化为：左右子树是否镜像。分解为：树1的左子树和树2的右子树是否镜像，树1的右子树和树2的左子树是否镜像。imooc符合“分、解、合”特性，考虑选择分而治之。

解题步骤分：获取两个树的左子树和右子树。解：递归地判断树1的左子树和树2的右子树是否镜像，树1的右子树和树2的左子树是否镜像。合：如果上述都成立，且根节点值也相同，两个树就镜像。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isSymmetric = function(root) {
    if(!root) return true;
    return isMirror(root.left, root.right);
};
function isMirror(left, right) {
    if(!left && !right) return true;
    if(!left || !right) return false;
    if(left.val !== right.val) return false;
    // 判断左右子树是否对称 (左子树的左节点和右子树的右节点, 左子树的右节点和右子树的左节点)
    return isMirror(left.right, right.left) && isMirror(left.left, right.right);
}

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isSymmetric = function(root) {
    if(!root) return true;
    return isMirror(root.left, root.right);
};
function isMirror(left, right) {
    if(!left&&!right)return true;
    if(left&&right&&left.val===right.val&&isMirror(left.left,right.right)&&isMirror(left.right,right.left)){
        return true;
    }
    return false
}

'第12章 算法设计思想之“分而治之”/12-2 LeetCode：374. 猜数字大小 (2).mp4'
'第12章 算法设计思想之“分而治之”/12-3 LeetCode：226. 翻转二叉树.mp4'
'第12章 算法设计思想之“分而治之”/12-4 LeetCode：100. 相同的树 (2).mp4'
'第12章 算法设计思想之“分而治之”/12-5 LeetCode：101. 对称二叉树.mp4'
'第12章 算法设计思想之“分而治之”/12-6 分而治之-章节总结 (2).mp4'
'第12章 算法设计思想之“分而治之”/12-7 思考题.png'

'第13章 算法设计思想之“动态规划”/13-1 动态规划简介.mp4'

1、说出动态规划算法的套路步骤。

一、动态规划的三大步骤

动态规划，无非就是利用历史记录，来避免我们的重复计算。而这些历史记录，我们得需要一些变量来保存，一般是用一维数组或者二维数组来保存。下面我们先来讲下做动态规划题很重要的三个步骤，

第一步骤：定义数组元素的含义，上面说了，我们会用一个数组，来保存历史数组，假设用一维数组 dp[] 吧。这个时候有一个非常非常重要的点，就是规定你这个数组元素的含义，例如你的 dp[i] 是代表什么意思？

第二步骤：找出数组元素之间的关系式，我觉得动态规划，还是有一点类似于我们高中学习时的归纳法的，当我们要计算 dp[n] 时，是可以利用 dp[n-1]，dp[n-2]…..dp[1]，来推出 dp[n] 的，也就是可以利用历史数据来推出新的元素值，所以我们要找出数组元素之间的关系式，例如 dp[n] = dp[n-1] + dp[n-2]，这个就是他们的关系式了。而这一步，也是最难的一步，后面我会讲几种类型的题来说。

第三步骤：找出初始值。学过数学归纳法的都知道，虽然我们知道了数组元素之间的关系式，例如 dp[n] = dp[n-1] + dp[n-2]，我们可以通过 dp[n-1] 和 dp[n-2] 来计算 dp[n]，但是，我们得知道初始值啊，例如一直推下去的话，会由 dp[3] = dp[2] + dp[1]。而 dp[2] 和 dp[1] 是不能再分解的了，所以我们必须要能够直接获得 dp[2] 和 dp[1] 的值，而这，就是所谓的初始值。

1. 第一步骤：定义数组元素的含义

2. 第二步骤：找出数组元素之间的关系式

3. 第三步骤：找出初始值。

2、完成打家劫舍2,地址：https://leetcode-cn.com/problems/house-robber-ii/

213. 打家劫舍 II

var rob = function(nums) {
    if (!Array.isArray(nums) || nums.some(isNaN)) {
        throw new Error("Invalid input: nums must be an array of numbers");
    }

    const n = nums.length;
    if (n === 0) return 0;
    if (n === 1) return nums[0];

    function robHelper(arr) {
        let prev = 0, curr = 0;
        for (let num of arr) {
            let temp = Math.max(curr, prev + num);
            prev = curr;
            curr = temp;
        }
        return curr;
    }

    // Case 1: Do not rob the first house
    let case1 = robHelper(nums.slice(1));
    // Case 2: Do not rob the last house
    let case2 = robHelper(nums.slice(0, n - 1));

    return Math.max(case1, case2);
};

var rob = function(nums) {
    if (nums.length === 0) return 0;
    if (nums.length === 1) return nums[0];
    if (nums.length === 2) return Math.max(nums[0], nums[1]);

    let prev1 = 0,curr1=0;
    let prev2 = 0,curr2=0;
    
    for (let i = 1; i < nums.length; i++) {
        let current = Math.max(prev1, curr1 + nums[i]);
        curr1=prev1
        prev1=current
    }
    for (let i = 0; i < nums.length-1; i++) {
        let current = Math.max(prev2, curr2 + nums[i]);
        curr2=prev2
        prev2=current
    }
    return Math.max(prev1, prev2);
};

let nums = [1,2,3]
console.log(rob(nums))

inner loop

out loop v

动态规划是什么？动态规划是算法设计中的一种方法。它将一个问题分解为相互重叠的子问题，通过反复求解子问题，来解决原来的问题。

union inner move

斐波那契数列

定义子问题：F(n)=F(n-1)+F(n-2)。

反复执行：从2循环到n，执行上述公式。

动态规划vs.分而治之

LeetCode:70.爬楼梯

关系式 math….

解题思路爬到第n阶可以在第n-1阶爬1个台阶，或者在第n-2阶爬2个台阶。F(n) =F(n-1)+ F(n-2)。使用动态规划。

解题步骤定义子问题：F(n)=F(n-1)+F(n-2)。反复执行：从2循环到n，执行上述公式。

/**
 * @param {number} n
 * @return {number}
 */
var climbStairs = function(n) {
    if(n<2)return 1;
    let dp=[1,1];
    for(let i=2;i<=n;i++){
        dp[i]=dp[i-1]+dp[i-2]
    }
    return dp[n]
};

LeetCode:198.打家劫舍

解题思路f(k)=从前k个房屋中能偷窃到的最大数额。Ak=第k个房屋的钱数。

f(k) = max(f(k- 2) + Ak, f(k-1))。考虑使用动态规划。

1+2max1

math method true step 公式/+-p/pr

/**
 * @param {number[]} nums
 * @return {number}
 */
var rob = function(nums) {
    if(nums.length===0){return 0}
    let dp=[0,nums[0]]
    for(let i=2;i<=nums.length;i++){
        dp[i]=Math.max(dp[i-2]+nums[i-1],dp[i-1])
    }
    return dp[nums.length]
};

动态规划是什么？动态规划是算法设计中的一种方法。它将一个问题分解为相互重叠的子问题，通过反复求解子问题，来解决原来的问题。

337. 打家劫舍 III

var rob = function(root) {
    function dfs(node) {
        if (!node) return [0, 0]; // [不偷当前节点的最大金额, 偷当前节点的最大金额]

        const left = dfs(node.left);
        const right = dfs(node.right);

        // 如果不偷当前节点，那么可以偷或不偷左右子节点
        const notRobCurrent = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);

        // 如果偷当前节点，那么不能偷左右子节点
        const robCurrent = node.val + left[0] + right[0];

        return [notRobCurrent, robCurrent];
    }

    const result = dfs(root);
    return Math.max(result[0], result[1]);
};

function TreeNode(val, left, right) {
  this.val = val === undefined ? 0 : val;
  this.left = left === undefined ? null : left;
  this.right = right === undefined ? null : right;
}

function buildTree(preorder) {
  if (preorder.length === 0) return null;

  let root = new TreeNode(preorder[0]);
  let queue = [root];
  let i = 1;

  while (i < preorder.length) {
    let currentNode = queue.shift();

    if (preorder[i] !== null) {
      currentNode.left = new TreeNode(preorder[i]);
      queue.push(currentNode.left);
    }
    i++;

    if (i < preorder.length && preorder[i] !== null) {
      currentNode.right = new TreeNode(preorder[i]);
      queue.push(currentNode.right);
    }
    i++;
  }

  return root;
}
var rob = function (root) {
  if (!root) return 0;
  let evenSum = 0,
    oddSum = 0;
  function dfs(node, higt) {
    if (!node) return [0, 0]; //返回两个值：[偷当前节点的最大金额, 不偷当前节点的最大金额]
    // 递归计算左子树和右子树的最大金额
    let left = dfs(node.left, higt + 1);
    let right = dfs(node.right, higt + 1);
    // 如果偷当前节点，则不能偷其左右子节点
    const robThisNode = node.val + left[1] + right[1];
    // 如果不偷当前节点，则可以选择偷或不偷其左右子节点
    const notRobThisNode =
      Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
    if (higt % 2 === 0) {
      evenSum = Math.max(robThisNode, notRobThisNode);
    } else {
      oddSum = Math.max(robThisNode, notRobThisNode);
    }
    // 返回当前节点偷和不偷的最大金额
    return [robThisNode, notRobThisNode];
  }
  dfs(root, 0);
  return Math.max(evenSum, oddSum);
};

// 构建二叉树
let preorder = [4, 1, null, 2, null, 3];
let root = buildTree(preorder);
console.log(rob(root));

'第13章 算法设计思想之“动态规划”/13-2 LeetCode：70. 爬楼梯.mp4'
'第13章 算法设计思想之“动态规划”/13-3 LeetCode：198. 打家劫舍.mp4'
'第13章 算法设计思想之“动态规划”/13-4 动态规划-章节总结.mp4'
'第13章 算法设计思想之“动态规划”/13-5 思考题.png'

'第14章 算法设计思想之“贪心算法”/14-1 贪心算法简介.mp4'

贪心算法是什么？贪心算法是算法设计中的一种方法。期盼通过每个阶段的局部最优选择，从而达到全局的最优。结果并不一定是最优。

零钱兑换 天龙八部-珍珑棋局

1、说出贪心算法的套路步骤。

1. 建立数学模型来描述问题；
2. 把求解的问题分成若干个子问题； 对每一子问题求解，得到子问题的局部最优解；
3. 把子问题的局部最优解合成原来问题的一个解。

**数学归纳法 ** 交换论证法

贪心算法三步走

1. 转换问题：将优化问题转换为具有贪心选择性质的问题，即先做出选择，再解决剩下的一个子问题。
2. 贪心选择性质：根据题意选择一种度量标准，制定贪心策略，选取当前状态下「最好 / 最优选择」，从而得到局部最优解。
3. 最优子结构性质：根据上一步制定的贪心策略，将贪心选择的局部最优解和子问题的最优解合并起来，得到原问题的最优解。

解题心得
贪心算法的核心：局部最优，从而达到全局最优。
能满足从局部最优推导出全局最优质，即可用贪心算法。
贪心算法写法需要充分挖掘题目中条件，没有固定的模式。
因为无固定招式，所以贪心算法题需要一定的直觉和经验。
贪心算法的题，往往是思考上有一定难度，即我们并不知道应该用贪心算法去解题，但是写法上一般不难。
局部最优并不一定能推导出整体最优，不要因此陷进贪心算法的陷阱。

2、贪心算法总能求的最优解吗？

指在对问题求解时，不从整体最优上加以考虑，而总是做出在当前看来是最好的选择。也就是说，所做出的是在某种意义上的局部最优解。

贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择，选择的贪心策略必须具备无后效性，即某个状态只与它前面出现的状态有关，而独立于后面的状态。

贪心算法与动态规划的区别

1. 贪心算法的每一次操作都对结果产生直接影响，而动态规划则不是。
2. 贪心算法对每个子问题的解决方案都做出选择，不能回退；动态规划则会根据以前的选择结果对当前进行选择，有回退功能。
3. 动态规划主要运用于二维或三维问题，而贪心一般是一维问题。

贪心算法是什么？贪心算法是算法设计中的一种方法。期盼通过每个阶段的局部最优选择，从而达到全局的最优。结果并不一定是最优。

LeetCode:455.分饼干

解题思路局部最优：既能满足孩子，还消耗最少。先将“较小的饼干”分给“胃囗最小”的孩子。

解题步骤对饼干数组和胃口数组升序排序。遍历饼干数组，找到能满足第一个孩子的饼干。然后继续遍历饼干数组，找到满足第二、三、….、n个孩子的饼干。

/**
 * @param {number[]} g
 * @param {number[]} s
 * @return {number}
 */
var findContentChildren = function(g, s) {
    g.sort((a, b) => a - b)
    s.sort((a, b) => a - b)
    let i=0;
    s.forEach(item=>{
        if(item>=g[i]){
            i++
        }
    })
    return i
};
// let g = [1,2,3], s = [1,1]
let g = [1,2], s = [1,2,3]
console.log(findContentChildren(g, s)) //1

LeetCode：122.买卖股票的最佳时机II

math tc g4d ..

解题思路前提：上帝视角，知道未来的价格。局部最优：见好就收，见差就不动，不做任何长远打算。

解题步骤新建一个变量，用来统计总利润。遍历价格数组，如果当前价格比昨天高，就在昨天买，今天卖，否则就不交易。遍历结束后，返回所有利润之和。

/**
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function(prices) {
    let maxProfit = 0;
    for(let i = 1; i < prices.length; i++){
        if(prices[i] > prices[i-1]){
            maxProfit +=prices[i]- prices[i-1];
        }
    }
    return maxProfit;
};
let prices = [7,1,5,3,6,4]
console.log(maxProfit(prices))

var maxProfit = function(prices) {
    let dp=Array.from({length:prices.length},()=>new Array(2).fill(null));
    dp[0] =[-prices[0], 0]
    for(let i = 1; i < prices.length; i++){
        dp[i][0]=Math.max(dp[i-1][0], dp[i-1][1]-prices[i]); // 买入
        dp[i][1]=Math.max(dp[i-1][1], dp[i-1][0]+prices[i]); // 不买

    }
    return dp[prices.length-1][1];
};

4x

121. 买卖股票的最佳时机

/**
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function(prices) {
    let max=0;
    for(let i = 0; i < prices.length; i++){
        for(let j=i+1; j < prices.length; j++){
            let profit=prices[j]-prices[i];
            if(profit>max){
                max = profit;
            }
        }
    }
    return max;
};
var maxProfit = function(prices) {
    let max=0;
    let minPrice=Infinity;
    for(let i = 0; i < prices.length; i++){
        if(prices[i]<minPrice){
            minPrice=prices[i];
        }
        else if(prices[i]-minPrice>max){
            max = prices[i]-minPrice;
        }
    }
    return max;
};
let prices = [7,1,5,3,6,4]
console.log(maxProfit(prices))

123. 买卖股票的最佳时机 III

/**
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function(prices) {
    if(prices.length===1) return 0;
    let init=null
    /**
        dp[i][0]: 无操作; 
        dp[i][1]: 第一次买入；
        dp[i][2]: 第一次卖出；
        dp[i][3]: 第二次买入；
        dp[i][4]: 第二次卖出；
     */
    const dp=new Array(5).fill(init)
    dp[1]=-prices[0]
    dp[3]=-prices[0]
    for(let i=1;i<prices.length;i++){
        dp[1]=Math.max(dp[1],dp[0]-prices[i])
        dp[2]=Math.max(dp[2],dp[1]+prices[i])
        dp[3]=Math.max(dp[3],dp[2]-prices[i])
        dp[4]=Math.max(dp[4],dp[3]+prices[i])
    }
    return dp[4]
};  
// let prices = [3,3,5,0,0,3,1,4]
let prices = [1,2]
console.log(maxProfit(prices))

\188. 买卖股票的最佳时机 IV

类比j为奇数是买，偶数是卖的状态。

/**
 * @param {number[]} prices
 * @return {number}
 */
​    dp[0]: 无操作; 

​    dp[1]: 第一次买入；

​    dp[2]: 第一次卖出；

​    dp[3]: 第二次买入；

​    dp[4]: 第二次卖出；
	// 2*k+1 
var maxProfit = function(k, prices) {
    if(prices == null || prices.length < 2 || k == 0) return 0;
    let init=null
    const dp=new Array(2*k+1).fill(null)
    for(let i=1;i<=2*k;i+=2){
        dp[i]=-prices[0]
    }
    for(let i=1;i<prices.length;i++){
       for(let j=1;j<dp.length;j++){
           if(j%2) dp[j]=Math.max(dp[j],dp[j-1]-prices[i])
           else dp[j]=Math.max(dp[j],dp[j-1]+prices[i])
       }
    }
    return dp[2*k]
};  
// let prices = [3,3,5,0,0,3,1,4]
let k = 2, prices = [2,4,1]
console.log(maxProfit(k,prices))

…vjx

'第14章 算法设计思想之“贪心算法”/14-2 LeetCode：455. 分饼干.mp4'
'第14章 算法设计思想之“贪心算法”/14-3 LeetCode：122. 买卖股票的最佳时机 II.mp4'
'第14章 算法设计思想之“贪心算法”/14-4 贪心算法-章节总结.mp4'
'第14章 算法设计思想之“贪心算法”/14-5 思考题.png'

'第15章 算法设计思想之“回溯算法”/15-1 回溯算法简介 (2).mp4'

回溯算法是什么？回溯算法是算法设计中的一种方法。回溯算法是一种渐进式寻找并构建问题解决方式的策略。回溯算法会先从一个可能的动作开始解决问题，如果不行，就回溯并选择另一个动作，直到将问题解决。

什么问题适合用回溯算法解决？有很多路。这些路里，有死路，也有出路。通常需要递归来模拟所有的路。

cu3d3

全排列用递归模拟出所有情况。遇到包含重复元素的情况，就回溯。1收集所有到达递归终点的情况，并返回。

LeetCode:46.全排列

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function (nums) {
  let res = [];
  let compose = (path) => {
    if (path.length === nums.length) {
      res.push(path);
      return;
    }
    for (let i = 0; i < nums.length; i++) {
      if (!path.includes(nums[i])) {
        compose(path.concat(nums[i]));
      }
    }
  };
  compose([]);
  return res;
};
let nums = [1, 2, 3];
console.log(permute(nums));

解题步骤用递归模拟出所有情况。遇到包含重复元素的情况，就回溯。收集所有到达递归终点的情况，并返回。

时间复杂度：O（n！)，n！=1×2×3×..×（n-1)×n空间复杂度：O(n)

LeetCode:78.子集

解题思路要求：1、所有子集；2、没有重复元素。网信2268731有出路、有死路。考虑使用回溯算法。

解题步骤用递归模拟出所有情况。8731保证接的数字都是后面的数字。收集所有到达递归终点的情况，并返回。

时间复杂度：O(2^N)，因为每个元素都有两种可能（存在或不存在）空间复杂度：O（N)

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var subsets = function(nums) {
    let res = [];
    var backtrack=(path,length,start)=>{
        if(path.length===length){
            res.push(path)
            return
        }
        for(let i=start; i<nums.length; i++){
            backtrack([...path,nums[i]],length,i+1)
        }
    }
    for(let i=0; i<=nums.length; i++){
        backtrack([],i,0)
    }
    return res;
};
let nums = [1, 2, 3];
console.log(subsets(nums));

回溯算法是什么？回溯算法是算法设计中的一种方法。回溯算法是一种渐进式寻找并构建问题解决方式的策略。回溯算法会先从一个可能的动作开始解决问题，如果不行，就回溯并选择另一个动作，直到将问题解决。

回溯法的意思 回溯就是一种暴力搜索方法，穷举所有的可能。回溯是递归的副产品，只要有递归就有回溯。

回溯的套路

下面分别阐述三要素：

1、回溯函数的返回值一般为void，但是参数没有二叉树递归那么容易确定，一般就是先写逻辑，需要什么参数再传进来

2、终止条件也要因题而异。但是既然前面说了使用回溯解决的问题都能抽象为树形结构，那么搜索到叶节点就意味着必须返回上一级了（即开始回溯），对该节点采取某种操作（比如存起来）

3、回溯搜索逻辑：回溯法是在集合中递归搜索，集合大小就是数的宽度，递归的深度就是树的深度

回溯算法是一种通过尝试所有可能的解决方案来解决问题的方法，如果当前的选择证明不是解决方案的一部分，则“回溯”并撤销选择，然后尝试下一个选择。下面是用回溯算法解决迷宫问题的一般步骤描述：

1. 定义迷宫

• 确定迷宫的起点和终点。
• 迷宫由墙壁（不可通行）和路径（可通行）组成。

2. 初始化

• 创建一个栈用于保存路径上的坐标点。
• 将起点坐标加入到栈中，并标记为已访问。

3. 开始探索

• 当栈不为空时，继续探索。
• 取出栈顶的坐标点作为当前位置。
• 检查当前位置是否是终点；如果是，则找到一条通路，结束搜索。
• 如果当前位置不是终点，检查它四周相邻的格子（通常为上、下、左、右四个方向）。

4. 尝试移动

• 对于每个相邻且未被访问过的格子：
  • 如果该格子是路径（即不是墙），则将此格子压入栈中，并标记为已访问。
  • 继续以这个新的位置作为当前位置进行探索。

5. 回溯

• 如果当前位置的所有相邻格子都已经被访问过或都是墙壁，表示没有合法的下一步。
• 此时从栈中弹出当前位置（撤销选择），回溯到前一个位置，继续尝试其他可能的方向。

6. 结束条件

• 如果在任何时刻找到了到达终点的路径，则停止搜索，返回成功。
• 如果栈为空且仍未找到通路，则说明没有从起点到终点的路径，返回失败。

使用这种方法，回溯算法能够保证遍历所有可能的路径直到找到通往终点的路径或者确定没有这样的路径存在。请注意，在实际实现中，还需要考虑如何避免进入死循环，比如当迷宫设计不良导致某些区域可以无限来回移动时。

'第15章 算法设计思想之“回溯算法”/15-2 LeetCode：46. 全排列 (2).mp4'
'第15章 算法设计思想之“回溯算法”/15-3 LeetCode：78. 子集 (2).mp4'
'第15章 算法设计思想之“回溯算法”/15-4 回溯算法-章节总结 (2).mp4'
'第15章 算法设计思想之“回溯算法”/15-5 回顾与总结 (2).mp4'
'第15章 算法设计思想之“回溯算法”/15-6 思考题.png'

数据结构：栈、队列、链表、集合、字典、树、图、堆。算法：链表/树/图的遍历、数组的排序和搜索……算法设计思想：分而治之、动态规划、贪心、回溯。

数据结构：所有数据结构都很重要，跟前端最相关的是链表和树。算法：链表/树/图的遍历、数组的排序和搜索……设计思想：分而治之、动态规划较常考，贪心、回溯次之。

经验心得搞清楚数据结构与算法的特点和应用场景。用JS实现一遍，最好能用第二第三语言再实现一遍。学会分析时间/空间复杂度。提炼前端和算法的结合点，用于工作实战。

多刷题，最好能保证300道以上。多总结各种套路、模板。多阅读源码，比如React、Lodash、V8.………多实战，将数据结构与算法用于工作。

课程资料/使用教程（必看）.url
课程资料/使用说明.txt

枚举、递归 模拟….

一、枚举法

枚举法，本质上就是搜索算法。 基本思想： 枚举也称作穷举，指的是从问题所有可能的解的集合中一一枚举各元素。 用题目中给定的检验条件判定哪些是无用的，哪些是有用的。能使命题成立。即为其解。 优缺点： 优点：算法简单，在局部地方使用枚举法，效果十分的好 缺点：运算量过大，当问题的规模变大的时候，循环的阶数越大，执行速度越慢

二、递归法

递归法是设计和描述算法的一种有力的工具，它在复杂算法的描述中被经常采用。 设一个未知函数f，用其自身构成的已知函数g来定义, 上述这种用自身的简单情况来定义自己的方式成为递归定义。 3个要素： 递归边界：算法要有一个边界出口，能结束程序 参数收敛：每次调用参数都是收敛于递归边界 自身调用 递归函数常使用堆栈，算法效率低，费时和费内存 递归按其调用方式分为直接递归和间接递归。所谓直接递归是指递归过程P直接自己调用自己；间接递归是指P包含另一个过程D，D调用P。

五、模拟法

模拟法是最直观的算法，通常是对某一类事件进行描述，通过事件发生的先后顺序进行输入输出。模拟法只要读懂问题的要求，将问题中的各种事件进行编码，即可完成。 模拟法（Simulation）主要是在考验程式设计人员编写程式码的功力，而非考验程式设计者的急智和创意。Simulation可说是程式设计的基本功──问题说得清清楚楚，不用设计复杂的演算法，只要照着规定做就好。这类题目很适合程式设计的初学者。 Simulation的问题有时相当难缠。若是问题规定的错综复杂，那么写起程式码就会相当累人。若是一不小心犯了错误，只能望着那长篇大论、杂乱无章的程式码，从中找出错误所在，相当痛苦。 另外，有一些目前尚未解决的经典题目，像是著名的Josephus Problem，由于目前没有好的演算法，所以大家遇到了这种问题，就只能乖乖的照着题目的要求来做。这一类的题目也就变成了Simulation的题目。

逻辑代码实现/伪代码

五大基础算法（枚举、递归、分治、贪心、模拟）动态规划、回溯