FHQ(非旋Treap)
神级数据结构!!!
原理:
先说明一下思想:
假如给你一个序列,让你在序列中插入一个数,你怎么做?
很简单,用数组存下来,然后找到应该插入的位置,然后把这个位置往后的数整体向右平移,这样就空出来了一个位置,把要插入的数放进去即可。
但是很明显,复杂度是 \(O(n)\) 的。
给你 \(n\) 次操作就 \(O(n^2)\) 了。
而FHQ就是通过把一个序列在期望 \(O(log)\) 的复杂度内断开,然后按照题目要求操作,再合并。
比如说我们有一个序列:
我们现在要在 \(3\) 后面插入一个 \(9\),那么我们可以把序列从 \(3\) 后面断开
然后把 \(9\) 放到 \(3\) 后面。
再合并。
别小看了这个断开和合并操作,就是因为能在 \(log\) 的时间内完成这两个操作,才使得 FHQ 成为了神级数据结构,能像普通的平衡树一样维护值域,还能像线段树一样维护序列。
实现:
怎么实现这个思想呢?
我们一下子就想到了平衡树。
这东西的中序遍历本身就是我们要求的序列。
那我们该怎么对树操作才能做到单次 \(O(logn)\) 的时间内完成分裂和合并操作呢?
直接递归从中间劈开!!
然后就分成两部分了。
再递归合并。
然后就变回去了。
分裂(\(Split\)):
把一棵树分成两棵树。
两种方式,一种是按照子树大小,一种是按照权值。
先讲权值。
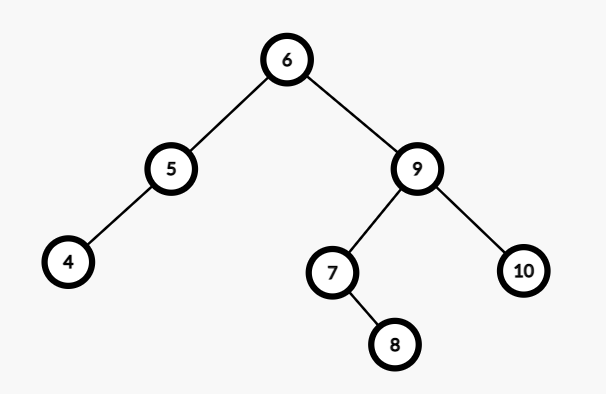
这个应该够复杂了。
假设我们要找大于等于 \(7\) 的数吧。
那就小于 \(7\) 的在一块,大于等于 \(7\) 的在一块。
已经说过了,这是个递归的过程。
从根开始。

可以看到,此刻 \(6\) 是小于 \(7\),所以它的左子树肯定都小于 \(7\).
直接全放到左树!!!。
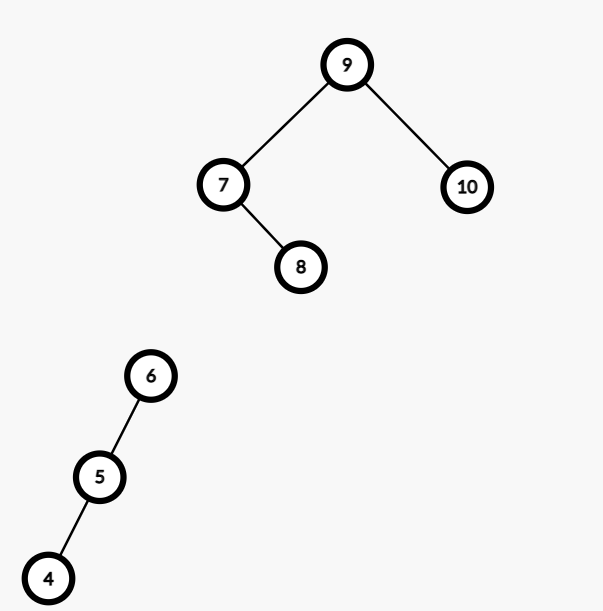
然后这个 \(9\) 比 \(7\) 大,所以右子树全比 \(7\) 大。
直接全放到右树!!
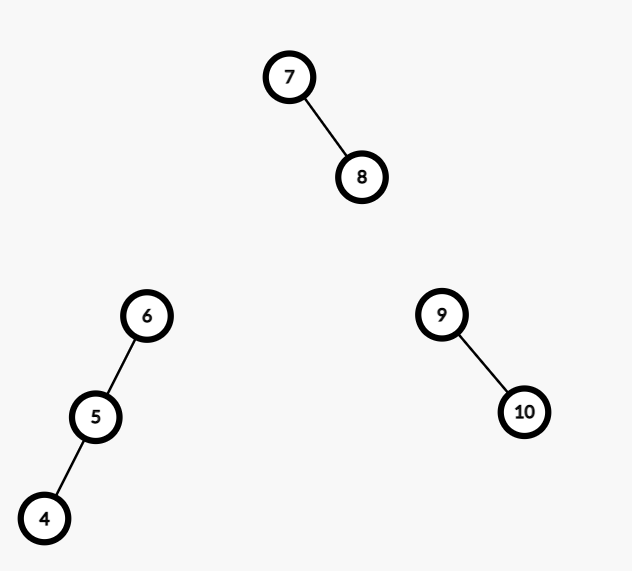
然后神奇的就来了。
\(7\) 等于 \(7\) 应该放到右树。
但是右树不为空,不能直接放,那怎么办呢。
我们可以发现一个很重要的性质。
从根一直递归下来的时候,我们如果遇到一个需要往右树放的情况,放的是当前最靠右的右子树。
也就是说,接下来再往右树放的时候,往右边放的这一部分在原序列中肯定在右树的左边。
而且因为我们每次是把右子树放过去了,所以左子树是空的。
这样一来……
直接接上去!!!
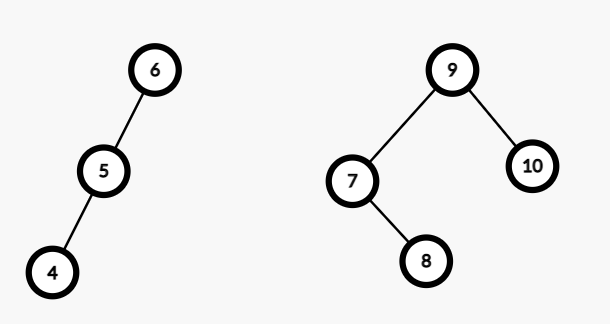
然后就分完了。
而且我们注意到,刚才的 \(7,8\) 填在了右树的左子树上,
按照我们的想法,接下来再往右树放的部分在原序列中肯定在更左边。
而我们发现,刚刚过来的部分根是 \(7\),它也是没有左子树的!!
如果是往左树放的话,是同理的。
于是……
你就会分裂了。
上代码:
void Split(int g, int &x, int &y, int val) {
if(g==0) {
x=y=0;//分裂完了。
return ;
}
if(t[g].val<val) {
x=g;//分到左子树。
Split(t[g].r, t[x].r, y, val);//继续分右子树,左树接下来要填充右子树。
}
else {
y=g;//同上
Split(t[g].l, x, t[y].l, val);
}
push_up(g);//别忘了更新信息。
}
根据子树大小分的话,也差不多啦其实。
把前 \(k\) 个分到一棵树里,剩下的分到另一棵树里。
会写普通平衡树的都知道要维护 \(k\)~。
void Split(int g, int &x, int &y, int k) {
if(g==0) {
x=y=0;
return ;
}
if(t[t[g].l].size+1<=k) {//如果根即左子树的大小在k之内
x=g;//去左树
Split(t[g].r, t[x].r, y, k-t[t[g].l].size-1);//还剩下这么多没去左边的。
}
else {//否则归右边。
y=g;
Split(t[g].l, x, t[y].l, k);
}
push_up(g);//维护信息。
}
好啦完美。
合并(\(Merge\))
合并这俩:

同时从两棵树的根开始走。

首先要知道,左树都是左子树过来的,右树都是右子树拼过来的。
所以,左树在原序列中一定在右树的右边,合并的时候只要保证左树合并上来后,中序遍历在左边,右树合并上来后中序遍历在右边就行了。
只要保证左右关系,上下关系是无所谓的。
那怎么合并才更好呢?
别忘了这是平衡树!!
而且 FHQ 是Treap 的一种!!
所以有随机权值。
我们就按照这个随机权值维护小根堆就好了。
如果左树的根权值小,左树的左子树上去,右子树和左树的右子树当合并后的右子树。
反之,右树的右子树先上去,左树和右树的左子树当合并后的左子树。看图理解:
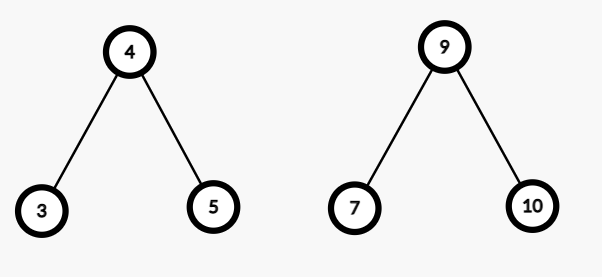
首先 \(4\) 的随机权值 \(1\) 比 \(9\) 的随机权值 \(2\) 小,先上去。

然后显然 \(9\) 再上去.

然后 \(7,5\) 依次上去.

\(NICE~!\)
代码实现:
int Merge(int x, int y) {//合并的两棵树(Merge函数返回根)
if(!x||!y) return x+y;//有一棵树为空,直接把另一棵合并上去。
if(t[x].ran<t[y].ran) {
t[x].r=Merge(t[x].r, y);//合并x的右子树和y
push_up(x);//更新信息
return x;//返回合并之后的根。
}
else {
t[y].l=Merge(x, t[y].l);
push_up(y);
return y;
}
}
到此,FHQ的两大核心操作就完成了。
基本所有操作都是通过这两个操作来进行的。
1.插入
如果是维护值域,就把小于等于这个数的部分放在左树,大于这个数的部分放在右树,
如果是维护序列,就从你想插入的位置劈开。
以上是分裂操作。
然后新建一个单一节点的树。
再把三棵树依次合并。
int New(int val) {
++head_size;//新节点
t[head_size].val=val;//权值
t[head_size].size=1;//初始树的大小
t[head_size].ran=rand();//随机权值
return head_size;
}
void insert(int val) {//(以按照权值分裂为例)
Split(rt, T1, T2, val);//分为两棵树
rt=Merge(Merge(T1, New(val)), T2);//依次合并
}
2.删除
通过分裂将你想要删除的节点甚至是部分序列提出来,然后把剩下的合并。
void Delet(int val) {
Split(rt, T1, T2, val);//小于等于val的放左树
Split(T1, T1, T3, val-1);//小于val的放左树
//等于val的都在T3了,把T1,T2合并。
rt=Merge(T1, T2);
}
3.查询x的排名。
把比x小的放在左树,直接返回左树大小+1,然后别忘了合并回去。
int Ranking(int val) {
Split(rt, T1, T2, val);//小于val的放左树
int k=t[T1].size;
rt=Merge(T1, T2);
return k+1;
}
4.查询排名为x的数
按照子树大小分裂,先把前x个提到左树。
然后把左树的最后一个提出来就是答案。
最后合并回去。
int find(int k) {
Split(rt, T1, T2, k);
Split(T1, T1, T3, k-1);
int re=t[T3].val;
rt=Merge(Merge(T1, T3), T2);
return re;
}
5.前驱
按照权值分裂。小于x的放在左树。
然后按照子树大小把最后左树的最后一个提出来。
int front(int val) {
Split1(rt, T1, T2, val-1);
Split2(T1, T1, T3, t[T1].size-1);
int re=t[T3].val;
rt=Merge(Merge(T1, T3), T2);
return re;
}
但是不想写这么多 \(Spilt\) 咋办。
也行,只需要对树多维护一个信息即 \(max\),然后直接返回最大值。
int front(int val) {
Split(rt, T1, T2, val-1);
int re=t[T1].max;
rt=Merge(T1, T2);
return re;
}
或者你也可以浅浅遍历一下左树,找到最右边的节点也就是最大值.
int Max(int g) {
while(g) {
if(t[g].r) g=t[g].r;
else return t[g].val;
}
}
int front(int val) {
Split(rt, T1, T2, val-1);
int re=Max(T1);
rt=Merge(T1, T2);
return re;
}
6.后继
同理。
而且,由于 FHQ 是一颗平衡树,如果你写普通的平衡树(Treap)写惯了,改不了了,那么普通平衡树的函数在FHQ里也都是适用的。
所以说这是一个很灵活很简洁很好用的神级数据结构!
缺点:
我们不难发现 FHQ 的每一个节点都只有一个数,如果序列里有相同的数,即使是维护值域我们也没有像 Treap 那样一个节点记录多个数。
所以,在某些数据范围下,FHQ 会建立更多的节点,由于都是均摊 log 的复杂度,速度上应该是相差不大。但是空间上可能会承受不住。
比如我要存 \(5e6\) 个数,其中会有一些重复的,
那么可能 Treap \(1e6\) 的空间维护的东西,FHQ 多开了五倍。
这么说你可能觉得空间这不都够吗。
但是别忘了一个节点要维护很多信息!!空间不止这么点!
那怎么办呢?
其实也很简单,只要你不怕麻烦,多写几行代码,其实也能写成一个点放多个数,这是完全没有问题的。
但是现在我要讲的是一种特殊情况。
有很多插入和删除,但是保证整个序列中的数的个数不超过一个范围
这个时候,如果我们一直无脑新建,那空间肯定会炸。
但是他说数的总个数有个范围。于是乎……
垃圾回收
建一个栈,维护能用的空间,序列中最多有几个数,我们就开个多大的栈。
每次取栈顶的的节点拿来新建。
删除了一个节点就将它入栈,然后就优化了空间。
一开始我们预处理:
for(int i=1; i<=MAXN; ++i) {
sta[++top]=i;
}
插入的时候就:
int New(int val) {
int g=sta[top--];//直接拿过来用
t[g].val=val;//权值
t[g].size=1;//初始树的大小
t[g].ran=rand();//随机权值
return g;
}
删除的时候就:
void Delet(int val) {
Split(rt, T1, T2, val);
Split(T1, T1, T3, val-1);
sta[++top]=T3;//直接进去。
rt=Merge(T1, T2);
}
当然 FHQ 还有很多用法。
他有时候还能当线段树用。
支持区间修改查询翻转。
天生自带可支持化。
………………
等等等等……
ORZ

