【BZOJ 2007】 2007: [Noi2010]海拔 (平面图转对偶图+spfa)
2007: [Noi2010]海拔
Time Limit: 20 Sec Memory Limit: 552 MB
Submit: 2504 Solved: 1195Description
YT市是一个规划良好的城市,城市被东西向和南北向的主干道划分为n×n个区域。简单起见,可以将YT市看作一个正方形,每一个区域也可看作一个正方形。从而,YT城市中包括(n+1)×(n+1)个交叉路口和2n×(n+1)条双向道路(简称道路),每条双向道路连接主干道上两个相邻的交叉路口。下图为一张YT市的地图(n = 2),城市被划分为2×2个区域,包括3×3个交叉路口和12条双向道路。 小Z作为该市的市长,他根据统计信息得到了每天上班高峰期间YT市每条道路两个方向的人流量,即在高峰期间沿着该方向通过这条道路的人数。每一个交叉路口都有不同的海拔高度值,YT市市民认为爬坡是一件非常累的事情,每向上爬h的高度,就需要消耗h的体力。如果是下坡的话,则不需要耗费体力。因此如果一段道路的终点海拔减去起点海拔的值为h(注意h可能是负数),那么一个人经过这段路所消耗的体力是max{0, h}(这里max{a, b}表示取a, b两个值中的较大值)。 小Z还测量得到这个城市西北角的交叉路口海拔为0,东南角的交叉路口海拔为1(如上图所示),但其它交叉路口的海拔高度都无法得知。小Z想知道在最理想的情况下(即你可以任意假设其他路口的海拔高度),每天上班高峰期间所有人爬坡所消耗的总体力和的最小值。Input
第一行包含一个整数n,含义如上文所示。接下来4n(n + 1)行,每行包含一个非负整数分别表示每一条道路每一个方向的人流量信息。输入顺序:n(n + 1)个数表示所有从西到东方向的人流量,然后n(n + 1)个数表示所有从北到南方向的人流量,n(n + 1)个数表示所有从东到西方向的人流量,最后是n(n + 1)个数表示所有从南到北方向的人流量。对于每一个方向,输入顺序按照起点由北向南,若南北方向相同时由西到东的顺序给出(参见样例输入)。Output
仅包含一个数,表示在最理想情况下每天上班高峰期间所有人爬坡所消耗的总体力和(即总体力和的最小值),结果四舍五入到整数。Sample Input
1
1
2
3
4
5
6
7
8Sample Output
3
【样例说明】
样例数据见下图。
最理想情况下所有点的海拔如上图所示。
对于100%的数据:1 ≤ n ≤ 500,0 ≤ 流量 ≤ 1,000,000且所有流量均为整数。
HINT
Source
【分析】
跟狼抓兔子差不多?
首先,大胆地考虑一下只有1和0?【如果不是,你可以假设一下只有一个点不是,周围都是,然后往好的地方修改,至少不会变差的】
当然你也不会无聊到1,0,1,0,交替。。不然累死人【其实最好就是都是平的,但是规定了两个角是有高度差的】
所以只要找到0,1分界线,就变成了最小割了。
但这种图嘛,可以转化成成对偶图,跑最短路就好了【别人说卡spfa?但是我过了】

1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<algorithm> 6 #include<queue> 7 using namespace std; 8 #define Maxn 510 9 10 int num[Maxn][Maxn],cnt; 11 12 struct node 13 { 14 int x,y,c,next; 15 }t[Maxn*Maxn*20]; 16 int first[Maxn*Maxn*2],len; 17 void ins(int x,int y,int c) 18 { 19 // printf("%d -> %d %d\n",x,y,c); 20 t[++len].x=x;t[len].y=y;t[len].c=c; 21 t[len].next=first[x];first[x]=len; 22 } 23 24 queue<int > q; 25 bool inq[Maxn*Maxn*4]; 26 int dis[Maxn*Maxn*4],st,ed; 27 bool spfa() 28 { 29 while(!q.empty()) q.pop(); 30 memset(inq,0,sizeof(inq)); 31 for(int i=1;i<=ed;i++) dis[i]=-1; 32 inq[st]=1;dis[st]=0; 33 q.push(st); 34 while(!q.empty()) 35 { 36 int x=q.front(); 37 for(int i=first[x];i;i=t[i].next) 38 { 39 int y=t[i].y; 40 if(dis[y]==-1||dis[y]>dis[x]+t[i].c) 41 { 42 dis[y]=dis[x]+t[i].c; 43 if(!inq[y]) 44 { 45 q.push(y); 46 inq[y]=1; 47 } 48 } 49 }q.pop();inq[x]=0; 50 } 51 if(dis[ed]==-1) return 0; 52 return 1; 53 } 54 55 int main() 56 { 57 int n; 58 scanf("%d",&n); 59 for(int i=1;i<=n;i++) 60 for(int j=1;j<=n;j++) num[i][j]=++cnt; 61 for(int i=1;i<=n;i++) num[i][0]=cnt+1; 62 for(int i=1;i<=n;i++) num[n+1][i]=cnt+1; 63 len=0; 64 memset(first,0,sizeof(first)); 65 for(int i=1;i<=n+1;i++) 66 for(int j=1;j<=n;j++) 67 { 68 int x;scanf("%d",&x); 69 ins(num[i-1][j],num[i][j],x); 70 } 71 for(int i=1;i<=n;i++) 72 for(int j=1;j<=n+1;j++) 73 { 74 int x;scanf("%d",&x); 75 ins(num[i][j],num[i][j-1],x); 76 } 77 for(int i=1;i<=n+1;i++) 78 for(int j=1;j<=n;j++) 79 { 80 int x;scanf("%d",&x); 81 ins(num[i][j],num[i-1][j],x); 82 } 83 for(int i=1;i<=n;i++) 84 for(int j=1;j<=n+1;j++) 85 { 86 int x;scanf("%d",&x); 87 ins(num[i][j-1],num[i][j],x); 88 } 89 st=0;ed=cnt+1; 90 // st=cnt+1;ed=0; 91 spfa(); 92 printf("%d\n",dis[ed]); 93 return 0; 94 }
2017-03-29 08:11:42
平面图转对偶图总结:
转自:http://blog.sina.com.cn/s/blog_60707c0f01011fnn.html
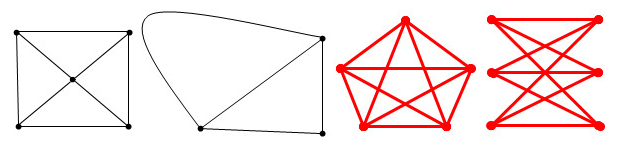
一个图G=(V,E),若能将其画在平面上,且任意两条边的交点只能是G的顶点,则称G可嵌入平面,或称G是可平面的。可平面图在平面上的一个嵌入称为一个平面图。如下图左边黑色的图为平面图,右边红色的图不属于平面图:
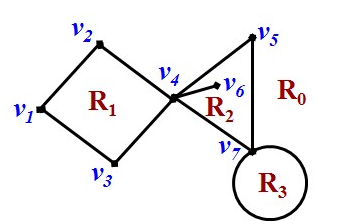
由平面图的边包围而成,其中不含图的顶点。也称为面。包围面R的所有边组成的回路称为该面的边界,回路长度称为该面的度,记为deg(R)。具有相同边界的面称为相邻面。由平面图的边包围且无穷大的面称为外部面。一个平面图有且只有一个外部面。如下面的平面图中,R0是外部面R0与R1, R2, R3均相邻。deg(R0)=8, deg(R1)=4, deg(R2)=5(R2经过的顶点序列为v7-v4-v6-v4-v5-v7), deg(R3)=1:
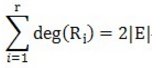
下面我们引入对偶图,设有平面图G=(V,E),满足下列条件的图G'= (V',E') 称为图G的对偶图:G的任一面Ri内有且仅有一点Vi';对G的域Ri和Rj的共同边界Ek,画一条边Ek'=(Vi',Vj')且只与Ek交于一点;若Ek完全处于Ri中,则Vi'有一自环Ek',如下图G'是G的对偶图:
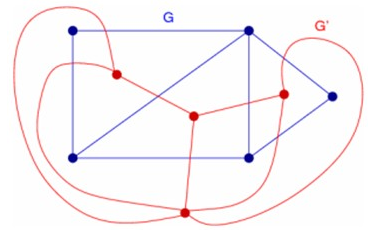
如果网络流中的图G可以转化为一个平面图,那么其对偶图G'中的环对应G中的割,利用最大流最小割定理转化模型,根据平面图G'与其对偶图的关系,先求出最小割。首先连接s和t,如下图蓝色虚线,得到一个附加面,我们设附加面对应的点为s',无界面对应的点为t',求该图的红色的对偶图G',最后删去s'和t'之间的边:
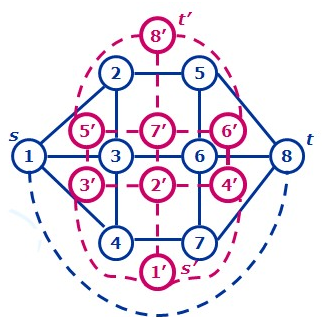
一条从s'到t'的路径,就对应了一个s-t割,更进一步,如果我们令每条边的长度等于它的容量,那么最小割的容量就等于最短路的长度。这样时间复杂度大大降低了。
注意 如果是有向边,那么就统一顺时针旋转90度


 浙公网安备 33010602011771号
浙公网安备 33010602011771号