【BZOJ 1038】 1038: [ZJOI2008]瞭望塔
1038: [ZJOI2008]瞭望塔
Description
致力于建设全国示范和谐小村庄的H村村长dadzhi,决定在村中建立一个瞭望塔,以此加强村中的治安。我们
将H村抽象为一维的轮廓。如下图所示 我们可以用一条山的上方轮廓折线(x1, y1), (x2, y2), …. (xn, yn)来描
述H村的形状,这里x1 < x2 < …< xn。瞭望塔可以建造在[x1, xn]间的任意位置, 但必须满足从瞭望塔的顶端可
以看到H村的任意位置。可见在不同的位置建造瞭望塔,所需要建造的高度是不同的。为了节省开支,dadzhi村长
希望建造的塔高度尽可能小。请你写一个程序,帮助dadzhi村长计算塔的最小高度。Input
第一行包含一个整数n,表示轮廓折线的节点数目。接下来第一行n个整数, 为x1 ~ xn. 第三行n个整数,为y1
~ yn。Output
仅包含一个实数,为塔的最小高度,精确到小数点后三位。
Sample Input
【输入样例一】
6
1 2 4 5 6 7
1 2 2 4 2 1
【输入样例二】
4
10 20 49 59
0 10 10 0Sample Output
【输出样例一】
1.000
【输出样例二】
14.500HINT
N ≤ 300,输入坐标绝对值不超过106,注意考虑实数误差带来的问题。
【分析】
还没有AC就打题解真的好?【默默对拍中。。
题目里面没有图,奉献一幅可爱的图?(这是样例1)
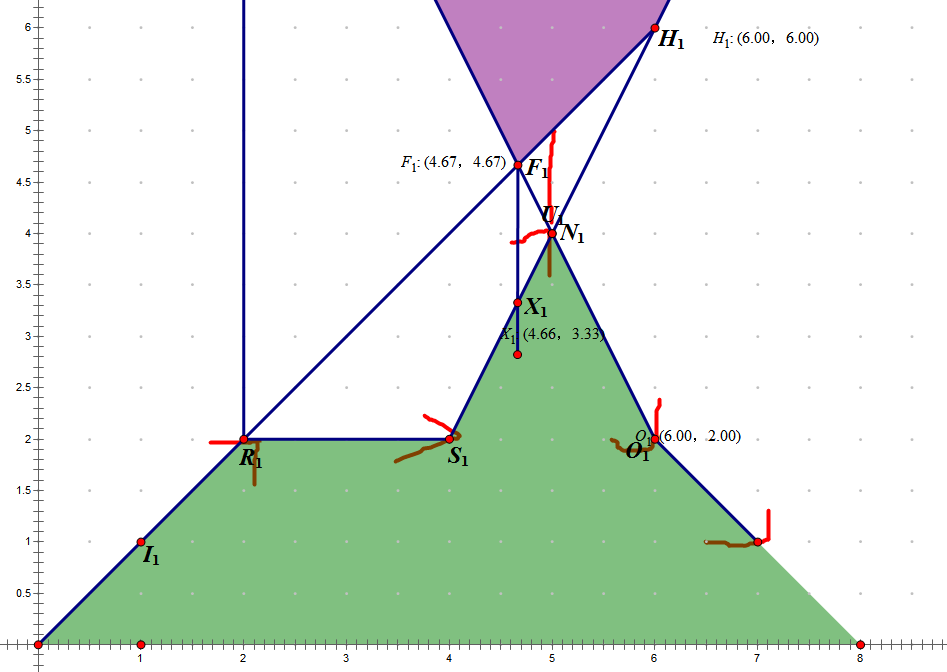
绿色是山,紫色是可行域,红色的是最小的塔高。
这题感觉吧跟多边形的核差不多,我们把轮廓线转换成半平面求角,然后考虑轮廓和半平面交的顶点(可以证明这里面一定存在最优塔高),
从这个顶点垂直于x轴延伸求出塔高,然后计算最小值就好了。
【1分钟后....
终于AC了,啊啊啊范围弄小了。。。。。10^6不是范围【没有听PO姐话就傻逼了一下
打半平面交的时候真是超级多错,最好弄eps搞精度。
然后注意轮廓和半平面交的边界(求塔高的时候不要越界,会有问题的)
就酱,真的是一周一题的缓慢速度。。。

1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<algorithm> 6 #include<cmath> 7 using namespace std; 8 #define Maxn 310 9 10 double INF=1e60; 11 const double eps=0.000001; 12 13 struct P {double x,y;}; 14 struct LN {P a,b;double slop;}l[Maxn],p[Maxn]; 15 16 double sx[Maxn],sy[Maxn]; 17 int n; 18 19 P operator - (P x,P y) 20 { 21 P tt; 22 tt.x=x.x-y.x; 23 tt.y=x.y-y.y; 24 return tt; 25 } 26 27 P operator + (P x,P y) 28 { 29 P tt; 30 tt.x=x.x+y.x; 31 tt.y=x.y+y.y; 32 return tt; 33 } 34 35 P operator * (P x,double y) 36 { 37 P tt; 38 tt.x=x.x*y; 39 tt.y=x.y*y; 40 return tt; 41 } 42 43 double Cross(P x,P y) {return x.x*y.y-x.y*y.x;} 44 double Dot(P x,P y) {return x.x*y.x+x.y*y.y;} 45 46 bool operator < (LN x,LN y) {return (x.slop==y.slop)?(Cross(x.b-x.a,y.b-x.a)<0):(x.slop<y.slop);} 47 48 P inter(LN x,LN y) 49 { 50 P nw=y.a-x.a; 51 double tt; 52 P X=x.b-x.a,Y=y.b-y.a; 53 tt=Cross(nw,X)/Cross(X,Y); 54 return y.a+Y*tt; 55 } 56 57 bool jud(LN x,LN y,LN z) 58 { 59 P nw=inter(x,y); 60 if(Cross(z.b-z.a,nw-z.a)<eps&&Cross(z.b-z.a,nw-z.a)>-eps) return 0; 61 return Cross(z.b-z.a,nw-z.a)<0; 62 } 63 64 int cnt; 65 void op() 66 { 67 for(int i=1;i<=cnt;i++) 68 { 69 printf("%.2lf %.2lf %.2lf %.2lf = %.2lf\n",l[i].a.x,l[i].a.y,l[i].b.x,l[i].b.y,l[i].slop); 70 }printf("\n"); 71 } 72 73 void opp(int L,int R) 74 { 75 for(int i=L;i<=R;i++) 76 { 77 printf("%.2lf %.2lf %.2lf %.2lf = %.2lf\n",p[i].a.x,p[i].a.y,p[i].b.x,p[i].b.y,p[i].slop); 78 }printf("\n"); 79 } 80 81 P as[Maxn]; 82 int L,R; 83 84 bool ffind() 85 { 86 for(int i=1;i<=n;i++) l[i].slop=atan2(l[i].b.y-l[i].a.y,l[i].b.x-l[i].a.x); 87 sort(l+1,l+1+n); 88 89 cnt=1; 90 for(int i=2;i<=n;i++) 91 { 92 if(l[i].slop!=l[cnt].slop) l[++cnt]=l[i]; 93 } 94 // op(); 95 L=1,R=2; 96 p[1]=l[1];p[2]=l[2]; 97 // opp(L,R); 98 if(cnt<2) return 0; 99 for(int i=3;i<=cnt;i++) 100 { 101 while(R>L&&jud(p[R],p[R-1],l[i])) R--; 102 while(R>L&&jud(p[L],p[L+1],l[i])) L++; 103 p[++R]=l[i]; 104 // opp(L,R); 105 } 106 if(R>L&&jud(p[R],p[R-1],p[L])) R--; 107 // opp(L,R); 108 if(R-L+1<2) return 0; 109 return 1; 110 // opp(L,R); 111 /*double ans=INF; 112 for(int i=L;i<R;i++) 113 { 114 P x=inter(p[i],p[i+1]); 115 ans=ans<x.y?ans:x.y; 116 } 117 printf("%.3lf\n",ans);*/ 118 } 119 120 void get_ans() 121 { 122 double ans=INF; 123 int ft=L; 124 P fx=inter(p[L],p[L+1]); 125 for(int i=1;i<=n+1;i++) 126 { 127 while(sx[i]>=fx.x&&ft<R) 128 { 129 ft++; 130 fx=inter(p[ft],p[ft+1]); 131 } 132 LN nw; 133 nw.a.x=sx[i];nw.a.y=sy[i]; 134 nw.b.x=sx[i];nw.b.y=sy[i]+1; 135 P xx=inter(nw,p[ft]); 136 ans=ans<xx.y-sy[i]?ans:xx.y-sy[i]; 137 // printf("==%.2lf\n",xx.y-sy[i]); 138 } 139 // printf("--%.2lf\n",ans); 140 141 ft=1; 142 LN now; 143 now.a.x=sx[1];now.a.y=sy[1]; 144 now.b.x=sx[2];now.b.y=sy[2]; 145 for(int i=L;i<R;i++) 146 { 147 P x=inter(p[i],p[i+1]); 148 if(x.x<sx[1]) continue; 149 while(x.x>=sx[ft+1]) 150 { 151 ft++; 152 if(ft>n) break; 153 // now.a.x=sx[ft];now.a.y=sy[ft]; 154 now.a=now.b; 155 now.b.x=sx[ft+1];now.b.y=sy[ft+1]; 156 } 157 if(ft>n) break; 158 LN nw; 159 nw.a=nw.b=x;nw.b.y=nw.b.y+1; 160 P xx=inter(nw,now); 161 ans=ans<x.y-xx.y?ans:x.y-xx.y; 162 // printf("==%.2lf\n",x.y-xx.y); 163 } 164 if(ans>=-eps&&ans<=eps) printf("0.000\n"); 165 else printf("%.3lf\n",ans); 166 } 167 168 int main() 169 { 170 scanf("%d",&n); 171 for(int i=1;i<=n;i++) scanf("%lf",&sx[i]); 172 for(int i=1;i<=n;i++) scanf("%lf",&sy[i]); 173 n--; 174 for(int i=1;i<=n;i++) 175 { 176 l[i].a.x=sx[i];l[i].a.y=sy[i]; 177 l[i].b.x=sx[i+1];l[i].b.y=sy[i+1]; 178 } 179 if(!ffind()) printf("0.000\n"); 180 else get_ans(); 181 return 0; 182 }
做几何题真的就不删调试了。
2016-12-29 17:09:28


 浙公网安备 33010602011771号
浙公网安备 33010602011771号