【acmm】一道简单的数学题
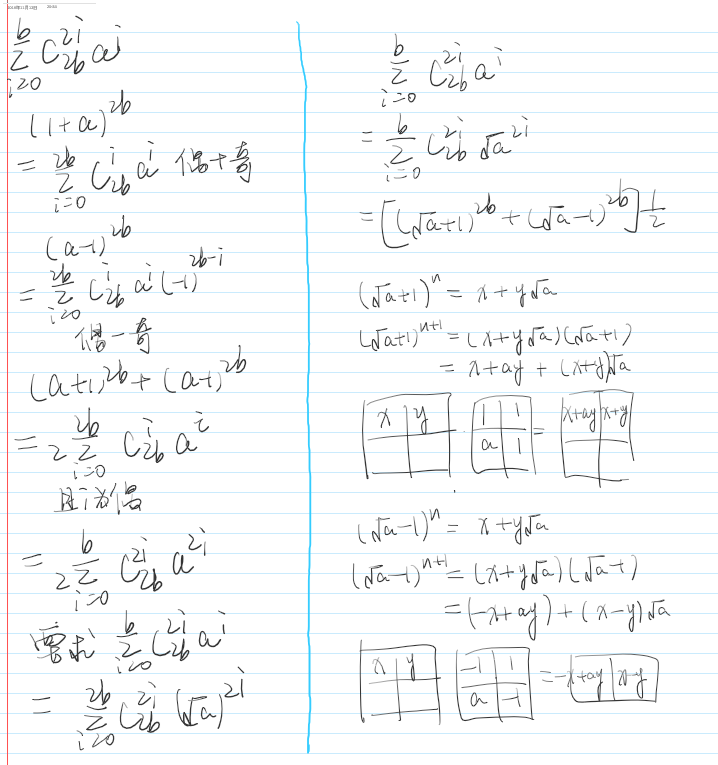
emm卡常
我本来写成了这个样子：
1 #include<bits/stdc++.h>
2 using namespace std;
3
4 typedef long long LL;
5 const LL mod = 1e9+7;
6 struct node{
7 LL s[5][5];
8 };
9 LL m0[2][2]={1,1,0,1};
10 LL m1[2][2]={-1,1,0,-1};
11
12 node mult(node x,node y)
13 {
14 node ans;
15 memset(ans.s,0,sizeof(ans.s));
16 for(int i=0;i<2;i++)
17 for(int j=0;j<2;j++)
18 for(int k=0;k<2;k++)
19 ans.s[i][j]=(ans.s[i][j]+(x.s[i][k]*y.s[k][j])%mod)%mod;
20 return ans;
21 }
22
23 node quickpow(node t,LL x)
24 {
25 node ans,now=t;
26 memset(ans.s,0,sizeof(ans.s));
27 ans.s[0][0]=ans.s[1][1]=1;
28 while(x)
29 {
30 if(x&1) ans=mult(ans,now);
31 now=mult(now,now);x/=2;
32 }
33 return ans;
34 }
35
36 int main()
37 {
38 //freopen("a.in","r",stdin);
39 //freopen("b.out","w",stdout);
40 int T;LL a,b;
41 scanf("%d",&T);
42 while(T--)
43 {
44 scanf("%lld%lld",&a,&b);
45 m0[1][0]=a;m1[1][0]=a;
46 node t0,t1;
47 for(int i=0;i<2;i++)
48 for(int j=0;j<2;j++)
49 {
50 t0.s[i][j]=m0[i][j];
51 t1.s[i][j]=m1[i][j];
52 }
53 t0=quickpow(t0,2*b-1);
54 t1=quickpow(t1,2*b-1);
55 LL ans=0;
56 ans=(((t0.s[0][0]+t0.s[1][0])%mod+(-t1.s[0][0]+t1.s[1][0])%mod)/2)%mod;
57 printf("%lld\n",ans);
58 }
59 return 0;
60 }
后来把矩乘全部直接改掉才a了
1 #include<bits/stdc++.h>
2 using namespace std;
3
4 typedef long long LL;
5 const LL mod = 1e9+7;
6 LL a,b,ans[2][2],now[2][2],p[2][2];
7
8 void quickpow(int tmp,LL x)
9 {
10 if(!tmp)
11 {
12 now[0][0]=1,now[0][1]=1;
13 now[1][0]=a,now[1][1]=1;
14 }
15 else
16 {
17 now[0][0]=-1,now[0][1]=1;
18 now[1][0]=a,now[1][1]=-1;
19 }
20 ans[0][0]=1,ans[0][1]=0;
21 ans[1][0]=0,ans[1][1]=1;
22 while(x)
23 {
24 if(x&1)
25 {
26 for(int i=0;i<2;i++)
27 for(int j=0;j<2;j++)
28 p[i][j]=ans[i][j];
29 ans[0][0]=(p[0][0]*now[0][0]+p[0][1]*now[1][0])%mod;
30 ans[0][1]=(p[0][0]*now[0][1]+p[0][1]*now[1][1])%mod;
31 ans[1][0]=(p[1][0]*now[0][0]+p[1][1]*now[1][0])%mod;
32 ans[1][1]=(p[1][0]*now[0][1]+p[1][1]*now[1][1])%mod;
33 }
34 for(int i=0;i<2;i++)
35 for(int j=0;j<2;j++)
36 p[i][j]=now[i][j];
37 now[0][0]=(p[0][0]*p[0][0]+p[0][1]*p[1][0])%mod;
38 now[0][1]=(p[0][0]*p[0][1]+p[0][1]*p[1][1])%mod;
39 now[1][0]=(p[1][0]*p[0][0]+p[1][1]*p[1][0])%mod;
40 now[1][1]=(p[1][0]*p[0][1]+p[1][1]*p[1][1])%mod;
41 x/=2;
42 }
43 }
44
45 int main()
46 {
47 //freopen("a.in","r",stdin);
48 int T;
49 scanf("%d",&T);
50 while(T--)
51 {
52 scanf("%lld%lld",&a,&b);
53 quickpow(0,2*b-1);
54 LL sum=(ans[0][0]+ans[1][0])%mod;
55 quickpow(1,2*b-1);
56 sum=((sum+(-ans[0][0]+ans[1][0])%mod)/2)%mod;
57 printf("%lld\n",sum);
58 }
59 return 0;
60 }
