Java基础排序算法实现（插入排序、冒泡、快排）

• 冒泡排序

 　　冒泡排序是基础排序算法之一，时间复杂度为O(n^2)。

　　简单的思路为，对于数组内的每一个索引（位置），分别将该位置上的元素与相邻下一个元素进行对比，若不满足排序要求，则调换位置。潜在的效果是，每一轮循环都能将数组的最值移到数组末尾。

　　

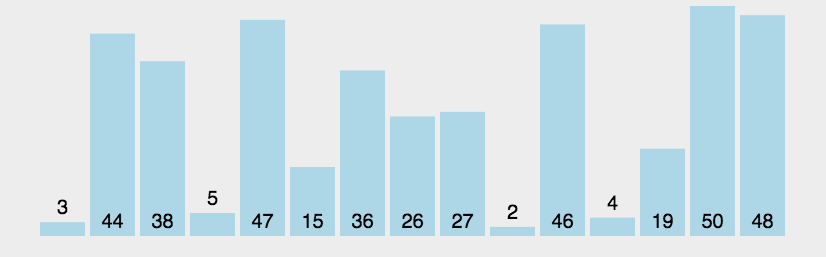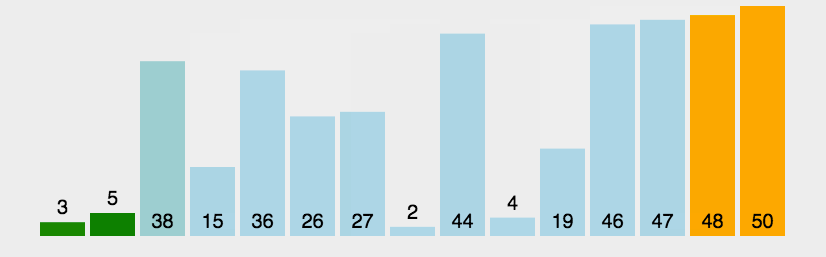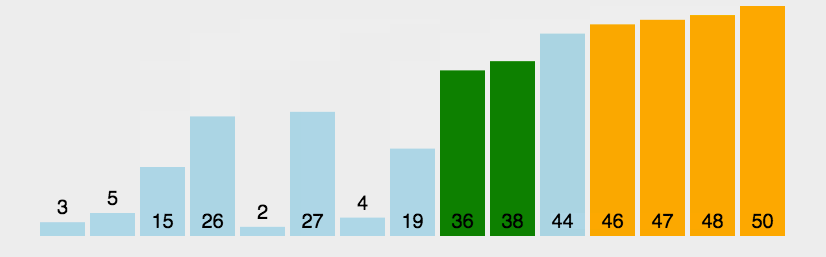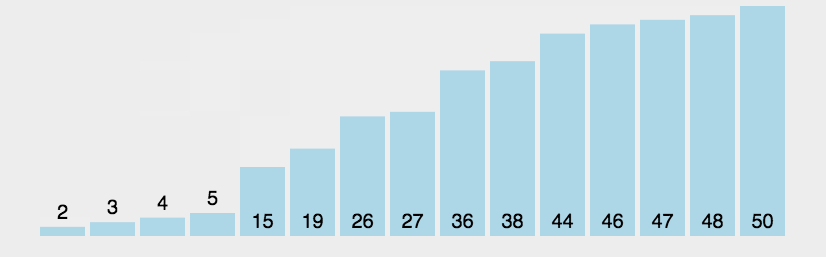
 　　代码示例：

public int[] bubbleSort(int[] nums) {
    int tmp = 0;
    for (int i = 0; i < nums.length - 1; i++) {
        boolean flag = false;
        for (int j = 0; j < nums.length - 1 - i; j++) {
            if (nums[j] > nums[j + 1]) {
                tmp = nums[j];
                nums[j] = nums[j + 1];
                nums[j + 1] = tmp;
                flag = true;
            }
        }
        if (!flag) {
            break;
        }
    }
    return nums;
}

 

• 插入排序

　　插入排序也属于比较基础的排序算法之一，处理大量数据时效率快于冒泡排序，最大时间复杂度为O(n^2)。

　　简单的思路为，从数组第二个元素 a_i （i >= 2）开始遍历，将a_i依次与其之前的所有元素进行对比，若不满足排序要求，则与对应位置元素进行调换。潜在效果是，每轮排序都可以将前i-1个元素排列好。

　   

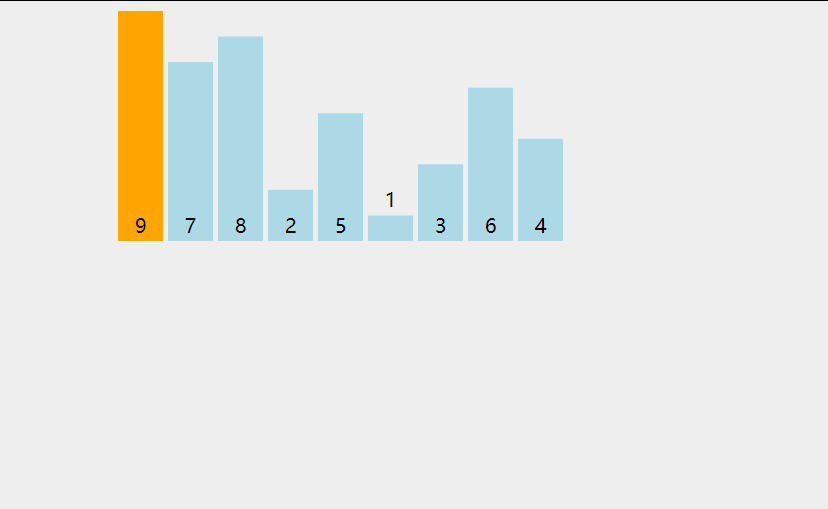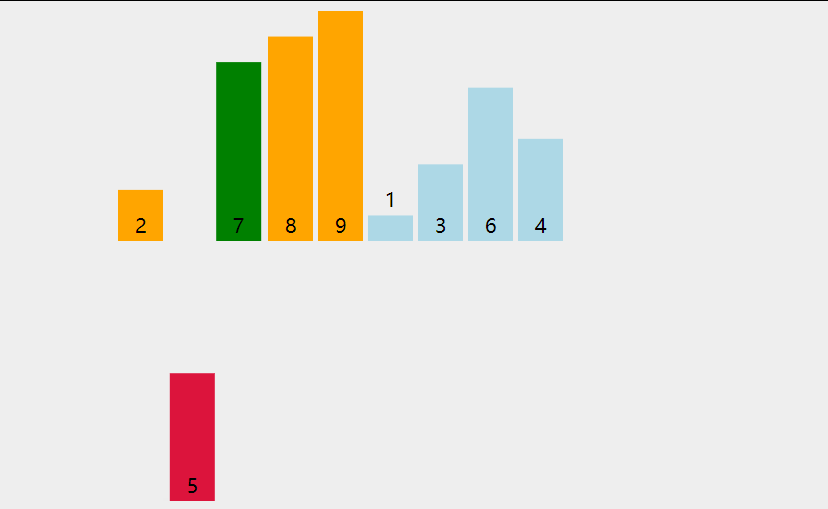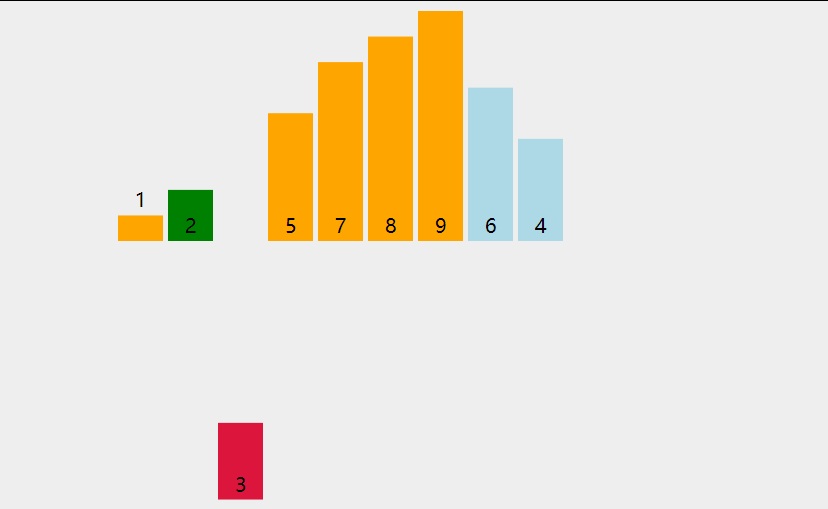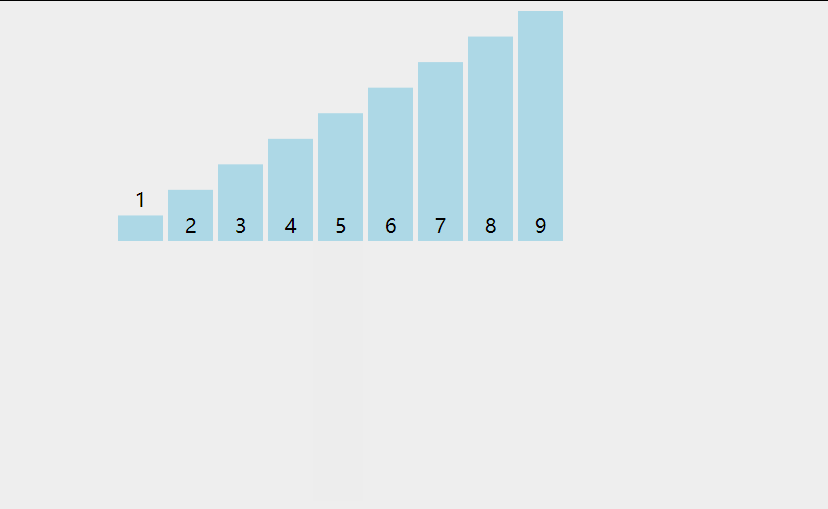
　　代码示例：

public int[] insertionSort(int[] nums){
    for (int i = 1; i < nums.length; i++) {
        int key = 0;
        int tmp = nums[i];
        for (int j = i; j > 0 && tmp < nums[j - 1]; j--){
            nums[j] = nums[j - 1];
            key = j;
        }
        if (nums[i] != tmp) {
            nums[key - 1] = tmp;
        }
    }
    return nums;
}

 

• 快速排序

　　快速排序是排序速度相对较快的算法之一，在时间复杂度同为O(nlogn)的排序算法中效率较高。

　　该算法的基本思想为：

　　1）先从数列中选取一个数作为基准数；

　　2）然后将数组中的数分别与基准数相比，比基准数大的元素放至数组末端，比基准数小的元素放至数组首端，这样数组就被分为了两部分；

　　3）再对两部分数组分别重复步骤1和2，直至最后分割的数组只有一个元素。

　　如此递归操作便实现了数组排序。

　　

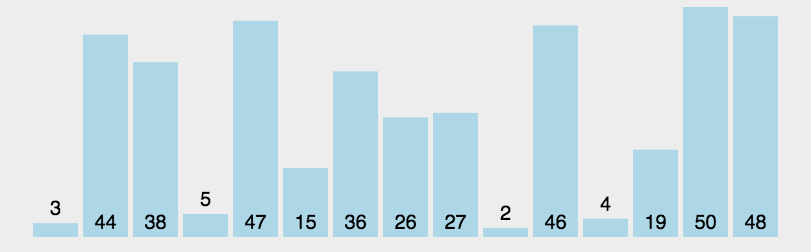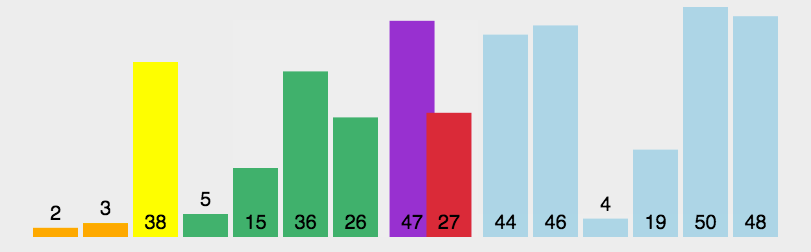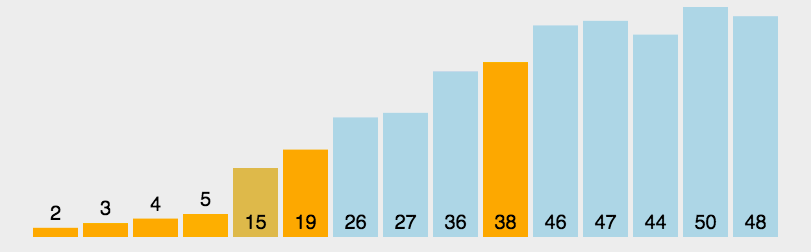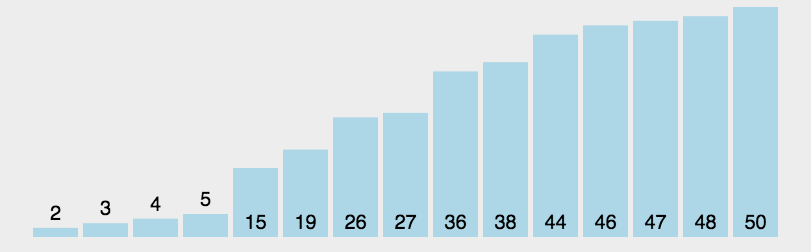
　　（其中黄色柱图表示基准数，绿色表示比基准数小的元素，紫色表示比基准大的数）

　　代码示例：

public int[] fastSort(int[] nums, int L, int R) {
    if(nums == null || nums.length < 2){
        return nums;
    }
    if (L < R){
        int mid = getMid(nums, L, R);
        fastSort(nums, L, mid -1);
        fastSort(nums, mid + 1, R);
    }
    return nums;
}
public int getMid(int[] nums, int L, int R){
    int tmp = nums[L]; //基准值
    while (L < R){
        while (L < R && nums[R] >= tmp){
            R--;
        }
        nums[L] = nums[R];
        while (L < R && nums[L] <= tmp){
            L++;
        }
        nums[R] = nums[L];
    }
    nums[L] = tmp;
    return L;
}

（以上动图均源自网络）