【图论系列-1】图论基础知识

如果大佬们发现错误请在评论区指出谢谢！

图

解决问题的模型

考虑这样一个问题：

幻想乡中有 \(n\) 个场所。有 \(m\) 条兽道，第 \(i\) 条兽道连接第 \(u_i\) 个场所和第 \(v_i\) 个场所。从兽道的一端可以花费 \(1\) 个小时到达另一端。

请问从幻想乡中的第 \(s\) 个场所到第 \(t\) 个场所，至少需要几个小时？

你会想要画一张“图”来直观地理解这个问题。除了想看起来更直观，你还想把它抽象成一个数学问题。

我们用一个“点”来表示幻想乡中的一个场所，而用一条“边”来表示一条兽道。

你给每个点编上号，于是画出了类似下图的一张图。

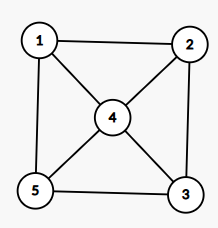
画一个数学上的点显然看不清，所以我们把它画大了。

图就是由若干个点与连接点与点的边构成的。通过将问题抽象成图，可以更直接地用数学方式解决问题。

有关图的基本知识

这个章节先不讨论如何解决图论问题。首先需要讨论一些基础的定义。

• 有向图和无向图
  无向图的每条边没有确定的方向；而有向图的每条边有确定的方向。
  例如刚才的问题，如果兽道是单行道，如果逆行会有城管罚款，你可以选择在图中建有向边表示它。从这个例子里可以看出，多数时候，无向边可以表示两个点互相指一条有向边。
• 路径
  想象你在图上“走路”，从某一个点出发，不断地通过某条边到另一个点。当你怎么做时，你可以用你依次经过的边来表示你走过的路，称为途径。
  如果你没有重复经过任何一个点，这条途径又称为路径。
  如果你从某个点出发走路回到了原来的点，且你没有重复经过任何一条边（可以经过同一个点），这条途径可以称为回路。
  如果一条回路在重新回到起点前没有重复经过任何一个点，这条回路称为环。
  还是这张图，\(1 \to 2 \to 4 \to 2 \to 3 \to 5 \to 4\) 是一条途径，但不是一条路径；\(1 \to 2 \to 4 \to 5 \to 3\) 是一条路径。 \(1 \to 4 \to 5 \to 1\) 是一个回路，也是一个环；\(4 \to 1 \to 5 \to 4 \to 3 \to 2 \to 4\) 也是一个回路，因为它没有重复经过某条边；但它不是一个环。
  
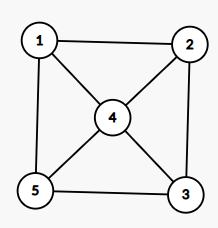
• 自环和重边
  如果图中一条边的两端是同一个点（没错，完全可以这样做），那么这条边称为自环。（其实就是由 \(1\) 条边组成的环。）
  如果图中两条边都连接者同样的两个点，那么这两条边称为一组重边。
  自环和重边又是对做题没有影响，但是有时会有影响。这时你需要手动去掉它们，或对它们做出一些特殊的判断。
• 连通性
  如果存在一条从 \(u\) 出发到 \(v\) 的途径，称 \(u\) 和 \(v\) 是连通的。
  如果一张图中所有点两两连通，那么图是一张连通图。
  假如图不连通，例如下图，应当怎么处理它？
  
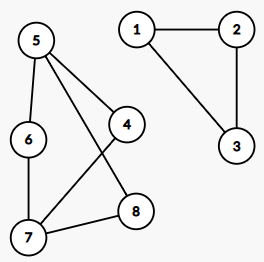
  发现这样的图都可以被拆成若干个部分，每个部分都是一个连通图，这每个部分都是原图的一个连通块。处理非连通图的时候，一般分别处理连通块就好了。
  连通图只有一个连通块。
• 度数
  对于无向图，一个点连接的边的数量称为这个点的度。
  对于有向图，从一个点连出的边的数量称为这个点的出度；连入一个点的边的数量称为这个点的入度。

树

树是一个没有环的连通无向图。得名的原因是将它吊起来的时候看起来像一棵倒挂的树，如下图。

树有下面的性质：

• 边数比点数少 \(1\)。
• 任意两个节点之间恰有一条路径。

有关树的基本知识

• 森林指的是每个连通块都是树的图。即一个没有环的无向图，不一定连通。
• 有根树和无根树
  没有固定根结点的树称为无根树。在无根树的基础上，指定一个结点称为根，则形成一棵有根树。
• 关于有根树的一系列定义
  用这张图辅助理解。
  
  将这张图看做一个“家谱”。根节点是先祖，其他点是它的子孙。边表示父子关系。
  定义点的深度为该点到根节点的路径上的边数，也就是“辈分”。
  定义树的高度为所有节点的深度最大值，理解为“几世同堂”。
  一条边深度小的一端是深度大的一端的父亲，反之则是儿子。一个点的所有儿子互为兄弟。
  如果节点 \(u\) 是节点 \(v\) 的父亲的父亲的 \(\dots\) 的父亲，（也就是说 \(u\) 在 \(v\) 到根节点的路径上）称 \(u\) 是 \(v\) 的祖先，或 \(v\) 是 \(u\) 的后代。
  一个点本身及它的所有后代组成它的子树。这样理解：假如它与父亲“断绝来往”，将它与父亲的边删掉，它和它的后代会自己形成一个新的“家谱”。特别地，根节点的子树是原树。