题解 【分裂游戏】

原题链接：Link

前言

考验思维难度的题，还是挺有意思的。

题目分析

第一眼看数据范围便知道这题不简单，DFS与BFS做在 \(1000\) 的范围内必定炸、

然后考虑规律。

当 \(n=1\) 与 \(n=2\) 的情况样例已经有给出，下面我们借助当 \(n=3\) 时的情况来推导一下。

下面请自行观赏下面的每一步推导。

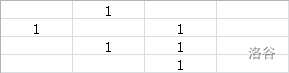
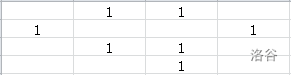
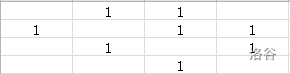
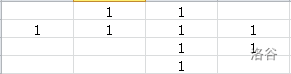
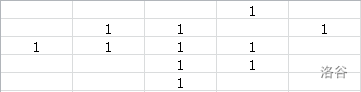
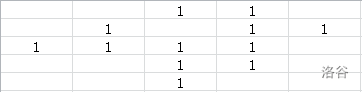
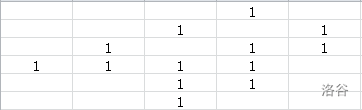
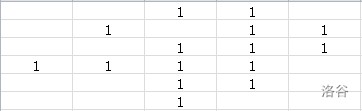
到此我们已经可以发现我们很难继续模拟了。我们发现要为一个棋子开道，其他子又会成为下一个等着被开道的子，就像递归。

到此我们开始思考规律，并先猜想：\(n>=3\) 时无解、

我们把 \((1,2)\) 与 \((2,1)\) 中的数标为 \(1/2\) ，把 \((1,3)\) 和 \((2,2)\) 和 \((3,1)\) 标为 \(1/4\) ，以此类推。

剩余的空格去减标号的总和，如果用 \(4\) 减出来的值小于 \(1\) ，那么就无解。

我们容易发现，第一行这无限个数的和应是 \(1+1/2+1/4+......\)

这些数的和无限接近于 \(2\) 。运用极限的思想我们把它看成 \(2\) 。

同理，第 \(2\) 行的和即是 \(1\) ，第 \(3\) 行为 \(1/2\) ，以此类推。

所以，这无限个数之和为 \(4\) 。

而我们已知无限分类的和应为 \(1\) 。

当 \(n=3\) 时，\(sum=1+1/2*2+1/4*3=11/4\)，\(4-11/4>=1\)，但与我们的猜想不符，我们接着继续分析。

但是，我们发现，第一行和第一列最多只能有一个数,所以此时的最大值为 \(5/4-1/8*2=1\) ，但在有限的操作中，我们不可能填满所有的格子，所以结果会小于 \(1\) 。与猜想相符合。

当 \(n=4\) 时，\(sum=1+1/2*2+1/4*3+1/8*4=13/4\) ，\(4-13/4=3/4<1\) ，与猜想相符合。

随着 \(n\) 的增大，数值会越来越小，因此不可能违反我们的猜想。

到此我们验证了我们猜想成立。

然后只用特判样例中的 \(n=1\) 与 \(n=2\) 的情况，其它全部输出 \(-1\) 即可。

代码不贴了，认真看到最后的读者应该会非常轻松打出代码。

如果还有什么不懂可以私信问我。

管理员审核辛苦了！