CF *3500

1. CF1336E2 Chiori and Doll Picking (hard version)

bitmasks, brute force, combinatorics, math。

https://www.luogu.com.cn/problem/CF1336E2。

题意：给你长度为 \(n\) 的数组 \(a_i\in[0,2^m)\)，对于每个 \(c\in[0,m]\) 求有多少个 \(a\) 的子序列，异或和的 popcount 为 \(c\)。

\(n\leq 200000,m\leq 53\)。

首先对 \(a\) 跑一个线性基 \(B\)，设 \(P=\operatorname{span}(B)\)，即 \(B\) 内向量张成的线性空间。那么，对于 \(i\in P\)，\(a\) 有恰好 \(2^{n-|B|}\) 个子序列异或和为 \(i\)（由线性基性质），于是我们将问题规模缩小到了 \(m\)，只用考虑 \(P\) 内的所有元素即可。

\(|B|\leq 26\)

这部分是简单的。可以 \(O(2^{|B|})\) dfs 出 \(P\) 中的每一个数，然后统计答案即可。

\(|B|>26\)

考虑能不能得到一个 \(O(2^{m-|B|})\) 的做法。

枚举 \(c\)，设 \(F[i]=[i\in P],G_c[i]=[\operatorname{popcount(i)}=c]\)，则我们要求 \(\sum F[i]G_c[i]\)，可以看做 \(F,G_c\) 做异或卷积取第 \(0\) 项：

\[(F*G_c)[0]=\operatorname{IFWT}(\operatorname{FWT}(F)\cdot \operatorname{FWT}(G_c))[0] \]

引理：\(\operatorname{FWT}(F)[i]=\sum_{j}(-1)^{j\operatorname{AND}i}F[j]\)。

然后我们发现 \(F[0]\) 对 \(\operatorname{FWT}(F)[i]\) 的贡献恒为 \(1\)，所以有：

引理：\(\operatorname{IFWT}(F)[0]=\dfrac 1{2^m}\sum_j F[j]\)。

代入：

\[\begin{aligned} (F*G_c)[0]&=\operatorname{IFWT}(\operatorname{FWT}(F)\cdot \operatorname{FWT}(G_c))[0]\\ &=\dfrac 1{2^m}\sum_{i=0}^m\left(\sum_{j=0}^m (-1)^{i\operatorname{AND}j}[i\in P]\right)\left(\sum_{j=0}^m(-1)^{i\operatorname{AND}j}[\operatorname{popcount}(j)=c]\right) \end{aligned}\]

后者，可以发现值只和 \(c,\operatorname{popcount}(i)\) 有关，具体地，枚举 \(\operatorname{popcount}(i\operatorname{AND} j)\)：

\[G(c,\operatorname{popcount}(i))=\sum_{j=0}^m\dbinom{\operatorname{popcount}(i)}{j}\dbinom{m-\operatorname{popcount}(i)}{c-j}(-1)^j \]

预处理即可。

前者，有个结论是：

\(\operatorname{FWT}(F)[i]=0\) 或者 \(2^{|B|}\)。具体地，当 \(i\) 与所有 \(y\in P\) 都有 \(2|\operatorname{popcount}(i\operatorname{AND} y)\)，取 \(2^{|B|}\) 否则是 \(0\)。

证明：

\(\operatorname{FWT}(F)\cdot\operatorname{FWT}(F) =\operatorname{FWT}(F*F)=2^{|B|}\operatorname{FWT}(F)\)，所以每一项要么是 \(0\)，要么是 \(2^{|B|}\)。然后，如果存在一个 \(y\) 使得 \(2|\operatorname{popcount}(i\operatorname{AND} y)\) 不成立，他就够不着 \(2^{|B|}\)，所以是 \(0\)；否则易证是 \(2^{|B|}\)。

所以我们只需要找到所有满足上述条件的 \(i\)，然后乘以 \(G(c,\operatorname{popcount}(i))\) 即可。

定义：正交补。在此处就是找到一个线性基 \(B'\)，他张成 \(P'\)，然后 \(\forall x\in P,y\in P'\) 有 \(2|\operatorname{popcount}(x\operatorname{AND}y)\)。注意，\(B'\) 不一定与 \(B\) 线性无关。

我们考虑如下图构造：

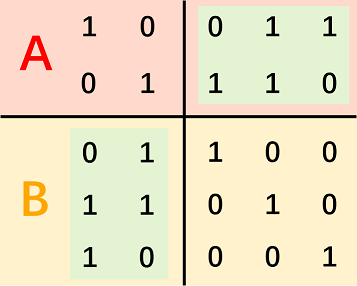
如果 \(B\) 不是连续的几行，做行列变换即可。

易证满足：对于 \(B'\) 内一个向量，与 \(B\) 内某向量，只会在交主对角线那两行对应的列处均为 \(1\)，否则其一一定为 \(0\)。然后由交换律可以得到所有 \(P'\) 内的都满足；然后证明至多只有 \(|P'|\) 个满足的，于是得证。

然后将找到的 \(P'\) 内元素逐个代入上式即可。复杂度 \(O(2^{m-|B|})\)。

https://codeforces.com/contest/1336/submission/341797365。