做题笔记 02
1. P13834 【MX-X18-T6】「FAOI-R6」Voices of the Chord
https://www.luogu.com.cn/problem/P13834。
题意:给定长度为 \(k\) 的正整数序列 \(b\),长度为 \(m\) 的集合序列 \(S\),\(S_i\) 内元素互不相同。在线维护长度为 \(n\) 的正整数序列 \(a\),支持操作:1. 给定 \(l,r,x\),\(\forall i\in[l,r],\forall j\in S_{b_i},a_j\leftarrow a_j+x\);2. 查询 \(\sum_{i\in[l,r]}a_i\)。
\(n,m,k,q\leq 10^5,\sum |S_i|\leq 3\times 10^5\)。
比较复杂的分块题。
Part 1. \(b\) 整块
对 \(b\) 分块,考虑整块部分,即 \(b\) 整块对 \(a\) 前缀的贡献,目标是可以 \(O(1)\) 查询。
求出 \(F_{i,j}\) 表示若一次 \(1\) 操作覆盖了 \(b\) 的第 \(i\) 个块(操作的 \(x=1\)),那么这次操作中 \(b\) 的第 \(i\) 个块对 \(a\) 前缀 \(j\) 的贡献系数。
求出 \(F\) 后整块的修改就可以绑定在 \(b\) 上了,具体的,维护 \(B_i\) 表示覆盖 \(b\) 上块 \(i\) 的 \(1\) 操作 \(x\) 的和。
然后查询 \(a_{[l,r]}\) 的时候就可以枚举 \(b\) 中的块 \(i\),然后累加 \((F_{i,r}-F_{i,l-1})B_i\)。
最后的问题是 \(F\) 怎么求。直接求的话复杂度容易爆炸,正确的做法是:枚举 \(b\) 块 \(i\),求出块内对于每个 \(j\),集合 \(S_j\) 出现了几次,然后枚举 \(j\in[1,m]\),\(S_j\) 内的元素,乘这个集合的出现次数,贡献到 \(a\) 对应位置,最后前缀和一下即可。
Part 2. \(b\) 散块
设 \(T_i\) 表示 \(i\) 出现在了哪些 \(S\) 中,\(T_i=\{j|i\in S_j\}\)。容易得到 \(\sum |T|=\sum |S|\),是可以接受的。
此时的一个可行的做法是:将修改绑定到 \(S\) 上。那么现在的修改和查询形如:
- \(\forall i\in[l,r], S_{b_i}\leftarrow S_{b_i}+x\);
- 求 \(\sum_{i\in[l,r]}\sum_{j\in T_i}S_j\)。
把 \(T\) 按照下标顺序合并为一个数组,查询容易改为:
- 求 \(\sum_{i\in[l,r]} S_{a_j}\)。
这个问题就比较可做了。具体的,首先按照 \(a\) 分块,然后还是考虑
\(b\) 的区间修改对 \(a\) 整块/散块的贡献。
此时修改操作的性质有:每次修改一段 \(b\) 下标连续段,长度小于块长。
Part 3. \(a\) 整块
求出 \(G_{i,j}\) 数组表示若进行一次 \(\forall i\in[1,j],S_{b_i}\leftarrow S_{b_i}+1\) 操作,\(a\) 的第 \(i\) 块的 \(\sum_{k\in Block(i)}S_{a_{k}}\),求的方法与 \(F\) 类似,同样注意不要使得复杂度退化。
然后每次修改时,可以直接枚举 \(a\) 的块然后贡献过去,具体的,修改 \(l,r,x\) 就可以枚举 \(i\),然后对 \(a\) 的第 \(i\) 块贡献 \(x(G_{i,r}-G_{i,l-1})\)。
Part 4. \(a\) 散块
注意到此时是 \(b\) 散块对 \(a\) 散块贡献,直接记录即可。
//P13834
#include <bits/stdc++.h>
using namespace std;
const int B = 1000;
int n, K, m, q, b[100010], a[300010];
vector<int> S[100010], T[100010];
unsigned int F[400][100010], G[400][100010];
int Binb[100010], Ble[100010], Bri[100010];
int le[300010], ri[300010];
int Ainb[300010], Ale[300010], Ari[300010];
unsigned int SS[100010], BB[400], AA[400];
int Scnt[100010];
int main(){
scanf("%d%d%d%d", &n, &K, &m, &q);
for(int i = 1; i <= K; ++ i){
scanf("%d", &b[i]);
Binb[i] = (i - 1) / B + 1;
if(Binb[i] != Binb[i-1]){
Bri[Binb[i-1]] = i-1;
Ble[Binb[i]] = i;
}
}
Bri[Binb[K]] = K;
for(int i = 1; i <= m; ++ i){
int sz;
scanf("%d", &sz);
for(int j = 1; j <= sz; ++ j){
int x;
scanf("%d", &x);
S[i].push_back(x);
T[x].push_back(i);
}
}
for(int i = 1; i <= Binb[K]; ++ i){
for(int j = Ble[i]; j <= Bri[i]; ++ j){
++ Scnt[b[j]];
}
for(int j = 1; j <= m; ++ j){
for(int k : S[j]){
F[i][k] += Scnt[j];
}
}
for(int j = 1; j <= n; ++ j){
F[i][j] += F[i][j-1];
}
for(int j = Ble[i]; j <= Bri[i]; ++ j){
-- Scnt[b[j]];
}
}
for(int i = 1, la = 0; i <= n; ++ i){
le[i] = la + 1;
ri[i] = le[i] + T[i].size() - 1;
la = ri[i];
for(int j = le[i]; j <= ri[i]; ++ j){
a[j] = T[i][j-le[i]];
}
}
for(int i = 1; i <= ri[n]; ++ i){
Ainb[i] = (i - 1) / B + 1;
if(Ainb[i] != Ainb[i-1]){
Ari[Ainb[i-1]] = i-1;
Ale[Ainb[i]] = i;
}
}
Ari[Ainb[ri[n]]] = ri[n];
for(int i = 1; i <= Ainb[ri[n]]; ++ i){
for(int j = Ale[i]; j <= Ari[i]; ++ j){
++ Scnt[a[j]];
}
for(int j = 1; j <= K; ++ j){
G[i][j] += Scnt[b[j]] + G[i][j-1];
}
for(int j = Ale[i]; j <= Ari[i]; ++ j){
-- Scnt[a[j]];
}
}
unsigned int la = 0;
while(q--){
int op, l, r;
unsigned int x;
scanf("%d%d%d", &op, &l, &r);
la &= 65535;
l ^= la;
r ^= la;
if(op == 1){
scanf("%u", &x);
if(Binb[l] == Binb[r]){
for(int i = l; i <= r; ++ i){
SS[b[i]] += x;
}
for(int i = 1; i <= Ainb[ri[n]]; ++ i){
AA[i] += x * (G[i][r] - G[i][l-1]);
}
} else {
for(int i = l; i <= Bri[Binb[l]]; ++ i){
SS[b[i]] += x;
}
for(int i = Ble[Binb[r]]; i <= r; ++ i){
SS[b[i]] += x;
}
for(int i = 1; i <= Ainb[ri[n]]; ++ i){
AA[i] += x * (G[i][Bri[Binb[l]]] - G[i][l-1]);
AA[i] += x * (G[i][r] - G[i][Ble[Binb[r]]-1]);
}
for(int i = Binb[l] + 1; i < Binb[r]; ++ i){
BB[i] += x;
}
}
} else {
la = 0;
for(int i = 1; i <= Binb[K]; ++ i){
la += BB[i] * (F[i][r] - F[i][l-1]);
}
l = le[l];
r = ri[r];
if(Ainb[l] == Ainb[r]){
for(int i = l; i <= r; ++ i){
la += SS[a[i]];
}
} else {
for(int i = l; i <= Ari[Ainb[l]]; ++ i){
la += SS[a[i]];
}
for(int i = Ale[Ainb[r]]; i <= r; ++ i){
la += SS[a[i]];
}
for(int i = Ainb[l] + 1; i < Ainb[r]; ++ i){
la += AA[i];
}
}
printf("%u\n", la);
}
}
return 0;
}
2. P13535 [IOI 2025] 纪念品(souvenirs)
https://www.luogu.com.cn/problem/P13535。
题意:交互题。有 \(n\) 件纪念品,价格分别为 \(P_0,P_1,...,P_{n-1}\),均为正整数且严格递减。交互库刚开始只给你 \(n\) 和 \(P_0\)。定义一次购买操作为:向交互库输出一个正整数 \(m\),交互库会执行:维护一个初始为空的 vector \(k\),将 \(i\) 从 \(0\) 到 \(n-1\) 遍历,若 \(m\geq P_i\),则将 \(i\) 插入 \(k\) 中,并且令 \(m\leftarrow m-P_i\),返回 \(k\) 以及最后的 \(m\) 值。你需要进行若干次购买操作,要求每次购买必须购买至少一件物品,若最后第 \(i\) 号物品恰好购买了 \(i\) 次,则通过题目(\(0\) 号物品当然只能购买 \(0\) 次)。
题目的限制其实非常严格,找到限制中唯一能走的一步跟着走就做完了。
首先,第一次询问肯定不能太小,否则买不到任何东西就寄了。于是选择询问 \(P_{0}-1\),这个数肯定不会出现问题。
然后,如果返回的那个集合中只有一个数价格没有确定,那么随之就确定了;否则有多个没有确定,可以知道他们的平均数,这个数肯定小于这个集合中价格最大的那个,考虑递归下去问这个平均数,求完这个集合内除掉最大值剩下的价格,就能确定最大值。
具体流程:定义函数 \(solve(x)\) 表示能够求得所有价格 \(\leq x\) 的纪念品的价格。初始调用 \(solve(P_0-1)\)。
- 购买 \(x\),得到一个集合 \(S\) 以及他们的平均值。
- 反复执行 3, 4 操作使得集合大小为 \(1\)。
- 将集合中那些已经确定价格的数删掉,更新平均值。
- 递归下去 \(solve\) 平均值,可以得到所有 \(\leq\) 平均值的价格,此时整个集合内已知价格一定会变多。
- 此时可以计算集合内唯一一个元素的价格(显然为价格最大的那个元素)。
- 找到后面所有的没有计算价格的元素中下标最小的一个 \(i\),调用 \(solve(P_{i-1}-1)\),因为此时 \(P_{i-1}\) 一定算过了。
可以发现,算法过程中以下标 \(i\) 作为最小下标的集合只有 \(1\) 个,所以此时每个物品的购买次数都是不大于题目要求的,然后知道所有价格后补全剩下的购买次数即可。
//P13535
#include <bits/stdc++.h>
using namespace std;
std::pair<std::vector<int>, long long> transaction(long long M);
int cnt[110], al;
typedef long long ll;
ll P[110];
void solve(ll val){
pair<vector<int>, ll> now = transaction(val);
for(auto i : now.first){
++ cnt[i];
}
vector<int> tmp;
for(auto i : now.first){
if(!P[i]){
tmp.push_back(i);
} else {
now.second += P[i];
}
}
swap(now.first, tmp);
int l = 0, r = now.first.size()-1;
while(l < r){
ll sum = val - now.second;
for(int i = r+1; i < now.first.size(); ++ i){
sum -= P[now.first[i]];
}
ll pj = sum / (r - l + 1);
solve(pj);
while(P[now.first[r]]){
-- r;
}
}
ll sum = val - now.second;
for(int i : now.first){
sum -= P[i];
}
P[now.first[0]] = sum;
for(int i = now.first[0] + 1; i < al; ++ i){
if(!P[i]){
solve(P[i-1] - 1);
break;
}
}
}
void buy_souvenirs(int N, ll P0){
al = N;
P[0] = P0;
cnt[0] = 0;
for(int i = 1; i < N; ++ i){
P[i] = cnt[i] = 0;
}
solve(P0 - 1);
for(int i = 1; i < N; ++ i){
while(cnt[i] < i){
transaction(P[i]);
++ cnt[i];
}
}
}
3. P13537 [IOI 2025] 世界地图(worldmap)
https://www.luogu.com.cn/problem/P13537。
给你一张 \(n\) 个点的无向连通图,要求构造一个 \(2n\times 2n\) 的矩形,每个元素 \(\in[1, n]\),要求:\(\forall u, v\in[1, n],u\neq v\),图中存在边 \((u,v)\) 等价于矩形中有两个边相邻的位置一个是 \(u\),一个是 \(v\)。
思路是现提取生成树,然后再塞进去非树边。
dfs 生成树性质是好的:如果把非树边绑到浅节点上,叶子节点不会有非树边,非叶子节点的非树边个数小于 \(siz\)。
构造方案:
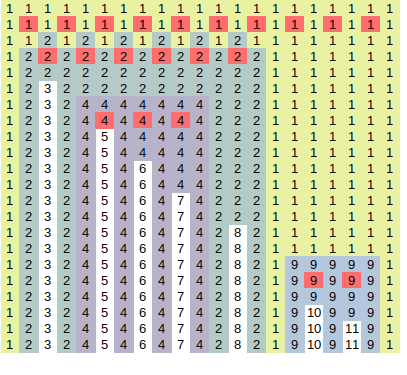
(最上面的 5 应该改为 4)
红色位置可以任意插入非树边。
//P13537
#include <bits/stdc++.h>
using namespace std;
vector<int> g[45], son[45];
int dfn[45], siz[45], dfc, st[45], stc, vis[45], fdf[45], dep[45];
void dfs(int x, int fa){
dep[x] = dep[fa] + 1;
vis[x] = 1;
dfn[x] = ++ dfc;
fdf[dfn[x]] = x;
siz[x] = 1;
st[x] = ++ stc;
for(int i : g[x]){
if(!vis[i]){
dfs(i, x);
++ stc;
siz[x] += siz[i];
} else if(i != fa && dep[x] > dep[i]){
son[i].push_back(x);
}
}
}
vector<vector<int> > create_map(int N, int M, vector<int> A, vector<int> B) {
vector<vector<int> > ans(2 * N, vector<int>(2 * N, 0));
dfc = stc = 0;
for(int i = 1; i <= N; ++ i){
vector<int> ().swap(g[i]);
vector<int> ().swap(son[i]);
vis[i] = dfn[i] = siz[i] = st[i] = fdf[i] = dep[i] = 0;
}
for(int i = 0; i < M; ++ i){
g[A[i]].push_back(B[i]);
g[B[i]].push_back(A[i]);
}
dfs(1, 0);
for(int i = 1; i <= N; ++ i){
for(int j = 2 * i - 2; j < 2 * N; ++ j){
for(int k = st[fdf[i]]-1; k <= st[fdf[i]] + 2 * siz[fdf[i]] - 3; ++ k){
ans[j][k] = fdf[i];
}
}
}
for(int i = 1; i <= N; ++ i){
for(int j = 0; j < siz[fdf[i]] - 1; ++ j){
ans[2*i][st[fdf[i]]+j*2] = fdf[i];
if(j < son[fdf[i]].size()){
ans[2*i-1][st[fdf[i]]+j*2] = son[fdf[i]][j];
}
}
}
for(int i = 0; i < 2 * N; ++ i){
ans[i][2*N-1] = 1;
}
return ans;
}
4. P13540 [IOI 2025] 羊驼的坎坷之旅(obstacles)
https://www.luogu.com.cn/problem/P13540。
题意:给一个 \(n\times m\) 的矩阵,每行一个权值 \(a\),每列一个权值 \(b\),一个格子可以走当且仅当 \(a_i>b_j\)。强制在线询问 \(L,R,S,T\),表示提取出 \([L,R]\) 内的列,点 \((0,S)\) 是否能四联通走到 \((0,T)\)。
\(n,m,q\leq 2\times 10^5\)。
首先不考虑 \(L,R\) 的限制。
不可行等价于有割。若将矩阵的左、下、右三面都加满一条障碍,那么割形如从 \((0,[S+1,T-1])\) 走到 \((0,[0,S-1])\) 或者 \((0,[T+1,m-1])\),可以证明这样的割一定是分为三段直线:向下、向两侧其中一侧、向上。
证明:首先每一列的障碍集合一定两两包含或者不交,然后画出一条不符合上述条件的折线 \((0,S)\to (0, T)\),可以证明要么存在一条满足上述条件的 \(S\to T\),要么存在若干条满足上述条件的 \(S\to P_1,...,P_k\to T\)。所以只用提取出所有满足上述条件的极小割即可。
发现,如果两个割区间有交,他们都不是极小的,所以极小割只有 \(O(n)\) 组。极小割是好求的:对于 \(b_i\),找到它两侧第一个 \(\geq b_i\) 的位置,然后 check \(i\) 和这两个位置分别能不能构成割即可。
考虑 \(L,R\) 的限制,多了一种情况是 \(L,R\) 与原先不是割的一段构成割,此时维护 \(mxl,mxr\) 表示 \(b_i\) 向下后再向两侧最远能够到达哪两列,然后 rmq 即可。
//P13540
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int a[N], b[N], n, m;
int lm[N], rm[N], st[N], tp;
int mxle[N], mxri[N], mxdn[N];
int apmx[N], apmn[N];
int ST[20][N];
int qmn(int l, int r){
int k = 31 ^ __builtin_clz(r - l + 1);
return min(ST[k][l], ST[k][r-(1<<k)+1]);
}
int mn[N*4], mx[N*4], mmn[N*4], mmx[N*4];
void add(int p, int l, int r, int x, int v, int op){
if(l == r){
if(op == 0){
mn[p] = min(mn[p], v);
} else if(op == 1){
mx[p] = max(mx[p], v);
} else if(op == 2){
mmn[p] = min(mmn[p], v);
} else if(op == 3){
mmx[p] = max(mmx[p], v);
}
} else {
int mid = l + r >> 1;
if(x <= mid){
add(p<<1, l, mid, x, v, op);
} else {
add(p<<1|1, mid+1, r, x, v, op);
}
mn[p] = min(mn[p<<1], mn[p<<1|1]);
mx[p] = max(mx[p<<1], mx[p<<1|1]);
mmn[p] = min(mmn[p<<1], mmn[p<<1|1]);
mmx[p] = max(mmx[p<<1], mmx[p<<1|1]);
}
}
int qry(int p, int l, int r, int ql, int qr, int op){
if(qr < l || r < ql){
return (op & 1) ? 0 : m + 1;
} else if(ql <= l && r <= qr){
if(op == 0){
return mn[p];
} else if(op == 1){
return mx[p];
} else if(op == 2){
return mmn[p];
} else {
return mmx[p];
}
} else {
int mid = l + r >> 1;
if(op & 1){
return max(qry(p<<1, l, mid, ql, qr, op), qry(p<<1|1, mid+1, r, ql, qr, op));
} else {
return min(qry(p<<1, l, mid, ql, qr, op), qry(p<<1|1, mid+1, r, ql, qr, op));
}
}
}
void initialize(vector<int> T, vector<int> H){
n = T.size(), m = H.size();
apmn[0] = 2e9;
for(int i = 1; i <= n; ++ i){
a[i] = T[i-1];
apmx[i] = max(a[i], apmx[i-1]);
apmn[i] = min(a[i], apmn[i-1]);
}
a[++n] = 0;
b[1] = b[m+2] = 1e9;
for(int i = 2; i <= m+1; ++ i){
b[i] = H[i-2];
}
m += 2;
for(int i = 1; i <= m; ++ i){
mn[i] = mn[i+m] = mn[i+m+m] = mn[i+m+m+m] = m + 1;
mmn[i] = mmn[i+m] = mmn[i+m+m] = mmn[i+m+m+m] = m + 1;
ST[0][i] = b[i];
int L = 0, R = n;
while(L < R){
int mid = L + R + 1 >> 1;
if(apmx[mid] <= b[i]){
L = mid;
} else {
R = mid - 1;
}
}
mxdn[i] = L;
}
for(int i = 1; i < 20; ++ i){
for(int j = 1; j + (1 << i) - 1 <= m; ++ j){
ST[i][j] = min(ST[i-1][j], ST[i-1][j+(1<<i-1)]);
}
}
tp = 0;
for(int i = 1; i <= m; ++ i){
int mn = apmn[mxdn[i]];
int L = 1, R = i;
while(L < R){
int mid = L + R >> 1;
if(qmn(mid, i) >= mn){
R = mid;
} else {
L = mid + 1;
}
}
mxle[i] = L;
L = i, R = m;
while(L < R){
int mid = L + R + 1 >> 1;
if(qmn(i, mid) >= mn){
L = mid;
} else {
R = mid - 1;
}
}
mxri[i] = L;
add(1, 1, m, i, mxle[i], 2);
add(1, 1, m, i, mxri[i], 3);
while(tp && b[st[tp]] < b[i]){
-- tp;
}
if(tp){
int mn = min(mxdn[i], mxdn[st[tp]]);
if(apmn[mn] <= qmn(st[tp], i)){
add(1, 1, m, i, st[tp], 0);
add(1, 1, m, st[tp], i, 1);
}
}
st[++tp] = i;
}
tp = 0;
for(int i = m; i >= 1; -- i){
while(tp && b[st[tp]] < b[i]){
-- tp;
}
if(tp){
int mn = min(mxdn[i], mxdn[st[tp]]);
if(apmn[mn] <= qmn(i, st[tp])){
add(1, 1, m, i, st[tp], 1);
add(1, 1, m, st[tp], i, 0);
}
}
st[++tp] = i;
}
}
bool can_reach(int L, int R, int S, int D){
if(S == D){
return 1;
}
if(S > D){
swap(S, D);
}
L += 1;
R += 3;
S += 2;
D += 2;
if(qry(1, 1, m, S+1, D-1, 0) < S){
return 0;
}
if(qry(1, 1, m, S+1, D-1, 1) > D){
return 0;
}
if(qry(1, 1, m, S+1, D-1, 2) <= L + 1){
return 0;
}
if(qry(1, 1, m, S+1, D-1, 3) >= R - 1){
return 0;
}
return 1;
}
5. P13606 [NWRRC 2022] IQ Game
https://www.luogu.com.cn/problem/P13606。
题意:一个 \(len\) 个点的环上有 \(n\) 个人,一个关键人,每个人都在一个点上。每次随机选一个环上的点,然后从这个点开始顺时针经过的第一个人离场,关键人离场后结束。求期望离场人数。
\(len\leq 10^9,n\leq 200\)。
\(O(n^4)\) 的歪解。
首先在关键人处断环为链,这样关键人就在序列的最后一个位置。
由期望线性性,期望离场人数等于枚举每个非关键人,这个人先于关键人离场的概率之和。
假设目前枚举到的人为 \(i\),然后枚举 \(i\) 离场时,在他左边操作的次数 \(x\);右边操作的次数 \(y\),如果能够求到 \(F\):左边操作 \(x\) 次,第 \(x\) 次使得人 \(i\) 离场;\(G\):右边操作 \(y\) 次,最后一个人不离场,那么答案是好算的,即:单个概率乘以考虑操作顺序后本质相同的方案数:
最后考虑 \(F,G\) 怎么求了,容易发现从后往前求是比较简单的:对于 \([i,n]\) 上的操作,只需满足 \([j,n]\) 操作数 \(\leq n-j\) 即可,那么记录 \(g_{i,j}\) 表示 \([i,n]\) 操作 \(j\) 次,最后一个人不离场的方案数:
\(G\) 取 \(g_{i+1,y}\) 即可。
\(F\) 同理,只不过要对于每个 \(i\) 从右往左算一次,取 \(f_{1,x-1}\times \dfrac{a_i}{len} - f_{1,x}\)。
复杂度瓶颈在于每次转移 \(F\)。可能可以通过转置之类的东西优化到三次方,但是我不会。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll P = 998244353;
const int N = 210;
int len, n, S, a[N];
ll C[N][N];
ll qp(ll x, ll y){
ll ans = 1;
while(y){
if(y & 1){
ans = ans * x % P;
}
x = x * x % P;
y >>= 1;
}
return ans;
}
ll f[N][N], g[N][N];
int main(){
scanf("%d%d%d", &len, &n, &S);
C[0][0] = 1;
for(int i = 1; i <= n; ++ i){
C[i][0] = 1;
for(int j = 1; j <= i; ++ j){
C[i][j] = (C[i-1][j] + C[i-1][j-1]) % P;
}
scanf("%d", &a[i]);
if(a[i] <= S){
a[i] += len - S;
} else {
a[i] -= S;
}
}
sort(a + 1, a + n + 1);
ll in = qp(len, P - 2);
g[n][0] = 1;
for(int i = n-1; i >= 1; -- i){
for(int j = 0; j <= n - i; ++ j){
ll val = 1;
for(int k = j; k >= 0; -- k){
g[i][j] = (g[i][j] + g[i+1][k] * val % P * C[j][k]) % P;
val = val * (a[i] - a[i-1]) % P * in % P;
}
}
}
ll ans = 0;
for(int i = 1; i < n; ++ i){
memset(f, 0, sizeof(f));
f[i][0] = 1;
for(int p = i-1; p >= 1; -- p){
for(int j = 0; j <= i - p; ++ j){
ll val = 1;
for(int k = j; k >= 0; -- k){
f[p][j] = (f[p][j] + f[p+1][k] * val % P * C[j][k]) % P;
val = val * (a[p] - a[p-1]) % P * in % P;
}
}
}
for(int x = 1; x <= i; ++ x){
for(int y = 0; y < n - i; ++ y){
ll F = (f[1][x-1] * a[i] % P * in % P - f[1][x] + P) % P;
ll G = g[i+1][y];
ans = (ans + C[x+y-1][y] % P * F % P * G) % P;
}
}
}
printf("%lld\n", (ans + 1) % P);
return 0;
}
6. P12573 [UOI 2023] An Array and XOR (NOIP T3)
https://www.luogu.com.cn/problem/P12573。
题意:给定一个整数 \(m\),一个长度为 \(n\) 的非负整数数组 \(a\),以及 \(q\) 个形如 \(l_i\), \(r_i\) 的查询。数组 \(a\) 的所有元素都小于 \(2^m\)。定义函数 \(f_i(x) = \min_{j \in [l_i, r_i]} (a_j \oplus x)\),其中 \(\oplus\) 表示按位异或运算。对于每个查询,你需要找到 \(\max_{x \in \{0, 1, \ldots, 2^m-1\}} f_i(x)\) 的值。
\(n\leq 10^5,m\leq 50,q\leq 5\times 10^5\)。
容易转化为:建 trie 树,\(a_i\) 的最大 \(x\) 是:代表 \(a_i\) 的那条链上,没有兄弟的点的权值和。
直接莫队可以做到 \(O(nm\sqrt q)\)。
优化是:对于每一位 \(j\),找到 \(le_i,ri_i\) 表示 \(i\) 两侧第一个在 \(j\) 位处分开的数,转化为二维数点问题。
7. P11714 [清华集训 2014] 主旋律
https://www.luogu.com.cn/problem/P11714。
题意:给你一张无重边自环的有向图 \(G(V,E)\),求 \(E\) 的子集 \(E'\) 数量,使得 \(G(V,E')\) 是强连通的。
\(n\leq 15\)。
设 \(E_{S,T}\) 表示 \(\sum_{i\in S,j\in T}[(i,j)\in E]\)。
首先考虑 DAG 计数:
设 \(f_S\) 表示 \(S\) 内的点构成 DAG 的方案数,转移的时候枚举 \(0\) 入度点集合 \(T\),那么 \(T\to S/T\) 的边可以任意连,\(T\) 内没有边,\(S\) 也为一个 DAG。但是不能保证所有 \(S/T\) 的点都有入度,所以需要容斥。
具体的,设 \(F_{T,S}\) 表示 \(S\) 内恰好 \(T\) 是 \(0\) 入度点集合的方案数;\(G_{T,S}\) 表示 \(S\) 内选定 \(T\) 是 \(0\) 入度点集合的方案数,则有:
子集反演:
使用 \(F\) 算 \(f\):
这也就是容斥系数是 \((-1)^{|T|+1}\) 的原因。
现在开始强连通图计数。忘记上述的状态定义,重新定义 \(f_S\) 为使得 \(S\) 为强连通图的方案数。
同样的,强连通图缩点后为一个点;否则为一个 \(\geq 2\) 个点的 DAG。枚举 \(0\) 入度 SCC 由 \(S\) 内的点构成。
如果直接定义 \(g_S\) 表示 \(S\) 内点构成若干个 SCC 的方案数的话,容斥系数 \((-1)^{|T|+1}\) 中的 \(|T|\) 代表 SCC 个数就无法表示了,所以我们考虑将容斥系数与 \(g\) 统一定义:\(g_{S}\) 表示 \(S\) 内点构成奇数个 SCC 方案数减去构成偶数个 SCC 方案数。
写出式子:
此时的 \(S/T\) 部分并没有要求是 DAG/SCC,而是任意一张图都可以。
注意到:此处 \(f\) 的式子有问题:如果将 \(g_S\) 带入 \(f_S\) 的式子中,两侧都出现了 \(f_S\)。但是考虑到此时的意义是:入度为 \(0\) 的 SCC 只有一个,且整张图由这一个 SCC 构成,不应该被带入到 \(f_S\) 的式子中。
解决方法是先当作 \(f_S=0\) 计算 \(g_S\),然后计算 \(f_S\),最后计算最终的 \(g_S\)。
最后问题:计算 \(E\)。观察到有用的 \(E_{A,B}\) 要么是 \(A=B\),要么是 \(A\cup B=S,A\cap B=\emptyset\)。
前者递推式:
后者,当计算到 \(S\) 时,递推:
总复杂度 \(O(3^n)\),空间 \(O(2^n)\)。
//P11714
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define ppc __builtin_popcount
const ll P = 1e9 + 7;
int n, m, in[15], out[15];
ll pw[220], E[1<<15], f[1<<15], g[1<<15], EE[1<<15];
int main(){
pw[0] = 1;
for(int i = 1; i < 220; ++ i){
pw[i] = pw[i-1] * 2 % P;
}
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; ++ i){
int x, y;
scanf("%d%d", &x, &y);
-- x;
-- y;
in[y] |= (1 << x);
out[x] |= (1 << y);
}
for(int S = 1; S < (1 << n); ++ S){
int x = 31 ^ __builtin_clz(S & -S);
E[S] = E[S^(1<<x)] + ppc(in[x]&S) + ppc(out[x]&S);
}
for(int S = 1; S < (1 << n); ++ S){
EE[S] = 0;
for(int T = (S - 1) & S; T; T = (T - 1) & S){
int x = 31 ^ __builtin_clz((S^T) & -(S^T));
EE[T] = EE[T^(1<<x)] + ppc(in[x]&T) - ppc(out[x]&(S^T));
if((S & -S) == (T & -T)){
g[S] = (g[S] - f[T] * g[S^T] % P + P) % P;
}
}
f[S] = pw[E[S]];
for(int T = S; T; T = (T - 1) & S){
f[S] = (f[S] - g[T] * pw[EE[T]] % P * pw[E[S^T]] % P + P) % P;
}
g[S] = (g[S] + f[S]) % P;
}
printf("%lld\n", f[(1<<n)-1]);
return 0;
}
8. P11834 [省选联考 2025] 岁月
https://www.luogu.com.cn/problem/P11834。
题意:给你一张 \(n\) 个点 \(m\) 条双向有向边的图 \(G\),每条有向边有 \(\dfrac 12\) 的概率消失,设得到的图为 \(G'\)。求图 \(G'\) 的最小外向生成树边权和等于 \(G\) 的的概率。
\(n\leq 15\)。特殊性质:边权 \(=1\)。
特殊性质
此时只要有外向生成树存在,则满足题意。
外向生成树存在等价于:
- 存在一个点集 \(C\),\(C\) 内点强连通,定义这个 \(C\) 为此时的根集。
- \(C\) 内点能到达 \(C\) 外所有点。
- \(C\) 外所有点到达不了 \(C\) 内任意一点。
三部分概率是独立的。
第一部分,等价于上一题主旋律,对于每个子集 \(S\) 求出其构成一个 SCC 的概率。
第二部分,考虑 dp。设目前枚举了点集 \(C\),\(dp_S\) 表示 \(C\) 能走到 \(S\) 内所有点的概率,容斥有一个集合 \(T\) 到达不了:
起始状态为 \(dp_C\) 为第一部分的答案,终点为 \(dp_U\)。
第三部分,答案就是 \(2^{-E_{U/C,C}}\),表示 \(U/C\to C\) 的边全部不能出现。
复杂度 \(O(4^n)\),瓶颈在于第二部分。
考虑转置原理:第二部分的转移,如果没有这个 \(1\),相当于 \(C\to U\) 的所有路径权值积的和。加上这个 \(1\) 就表示 \(C\to U\),每个中间点都能作为一次起点,所有路径权值积的和。
转置后就是所有 \(U\to P\) 的所有路径权值积的和,其中 \(P\) 能够到达 \(C\) 即可。
也就是一次 dp + 一次超集和。最后答案是每个 \(C\) 的上述三部分乘积加起来。复杂度 \(O(n^3)\)。
正解
kruskal 的结论是:任意一棵 MST,只提取 \(\leq w\) 的边,构成的连通块集合都是相同的。
那么,从小到大考虑每个边权,设目前考虑到边权 \(w\):
- 目前会形成若干个连通块,这个连通块形态只和原图形态有关。
- 设 \(bel_i\) 表示点 \(i\) 所在连通块点集。
- 设 \(sc_S\) 表示考虑边权 \(\leq x-1\) 时,集合 \(S\) 内的所有点所在连通块并集。
- 设 \(to_i\) 表示一端为 \(i\),边权为 \(w\) 的另一端点点集。
- 设 \(eg\_cnt_S\) 表示有多少条边权为 \(w\) 的边两端都在 \(S\) 内。
- 设 \(is_S\) 边权 \(w-1\to w\) 时,集合 \(S\) 所在连通块是否会改变(即这一轮这个集合是否需要计算)。
- 简单的计算:\(E(S,T)=eg\_cnt_{S|T}-eg\_cnt_S-eg\_cnt_T\)。
对于连通块 \(B\),它的内部集合 \(S\) 会以一个概率成为 \(B\) 内的根集,设为 \(ans_B\)(如果 \(B\) 不在一个连通块内,\(ans_B\) 看作未定义)
那么当考虑所有 \(w\) 边,我们需要做的是合并若干个连通块,然后更新 \(ans\) 数组。同样分为三部分:
Part 1. 点集 \(R\) 内部强连通
计算 \(R\) 与每一个连通块 \(B_i\) 的交集 \(R_i\),则相当于 \(R_1,...,R_k\) 这些各自连通块内的根集用连通块之间的 \(w\) 边实现强连通。和主旋律大体相同,区别在于 \(B_i/R_i\to R_j\) 的边也可以看作 \(R_i\to R_j\) 的边,因为 \(R_i\to B_i/R_i\) 必定可行。把 \(B_i\to R_j\) 称作对 \(i\to j\) 有用的边。修改主旋律转移式系数即可。
注意要求 \(sc_{S/T}\cap sc_T=0\),即 \(S/T,T\) 在不同的连通块内。此处的定义是 \(S/T\) 和 \(S\) 分别在不同 SCC 内,之间的所有有用的边都要断开。
此处要求 \(S/T\) 零入度。答案 \(f_R\)
Part 2. \(R\) 能到 \(sc_R\) 内所有点
设 \(dp_S\) 表示 \(R\) 能够走到 \(S\) 这个根集的概率(也就是说 \(R\) 能走到 \(sc_S\) 内所有点)。
这里需要考虑一下全集的概率,实际上是 \(S\) 在每个连通块内的部分都是根集的概率。设为 \(be_S= \prod ans_{S\operatorname{and}B_i}\)。
转移:
终点是所有 \(sc_S=sc_R\) 的 \(S\)。
转置方法是先找到这样的 \(S\) 然后令 \(dp_S=1\),接着倒着做这个 dp,然后每个位置 \(\times be_S\) 再贡献到它的子集作为答案的一部分。
Part 3. 没有边从完全与 \(R\) 不交的连通块里的点连进 \(R\)
对于 \(R\) 计算出这样连通块能连 \(cnt\) 条边,然后 \(\times 2^{-cnt}\) 即可。
最后用 \(dp_R\times 2^{-cnt}\times f_R\) 更新 \(ans_R\)。
最后答案是 \(\sum_{S\neq \emptyset} ans_S\)。
//P11834
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll P = 1e9 + 7;
ll pw[1000], ipw[1000];
ll qp(ll x, ll y){
ll ans = 1;
while(y){
if(y & 1){
ans = ans * x % P;
}
x = x * x % P;
y >>= 1;
}
return ans;
}
const ll i2 = qp(2, P - 2);
int n, m;
struct edge{
int u, v, w;
} eg[500];
bool cmp(edge x, edge y){
return x.w < y.w;
}
int fa[15];
int gf(int x){
return x == fa[x] ? x : fa[x] = gf(fa[x]);
}
ll ans[1<<15];//集合 S 作为根集概率
int sc[1<<15], new_sc[1<<15];//集合 S 所在连通块并集(本轮/下一轮)
int bel[15];//点 i 所在连通块集合
int to[1<<15];//点 i 邻域集合
ll be[1<<15];//集合 S 作为 sc_S 的根集的概率
int eg_cnt[1<<15];//集合 S 内目前需要考虑的边数
bool is[1<<15];//集合 S 目前是否需要考虑
ll f[1<<15], g[1<<15], dp[1<<15];
int E(int S, int T){//S,T 内边数
return eg_cnt[S|T] - eg_cnt[S] - eg_cnt[T];
}
void solve(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; ++ i){
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
eg[i] = {u - 1, v - 1, w};
}
sort(eg + 1, eg + m + 1, cmp);
for(int i = 0; i < n; ++ i){
fa[i] = i;
ans[1<<i] = 1;
bel[i] = 1 << i;
}
for(int S = 0; S < (1 << n); ++ S){
new_sc[S] = S;
}
for(int l = 1, r = 1; l <= m; l = r + 1){
r = l;
while(r + 1 <= m && eg[r+1].w == eg[l].w){
++ r;
}
swap(sc, new_sc);
memset(new_sc, 0, sizeof(new_sc));
memset(is, 0, sizeof(is));
memset(to, 0, sizeof(to));
for(int i = l; i <= r; ++ i){
if(gf(eg[i].u) != gf(eg[i].v)){
bel[gf(eg[i].v)] |= bel[gf(eg[i].u)];
fa[gf(eg[i].u)] = gf(eg[i].v);
}
to[eg[i].u] |= 1 << eg[i].v;
to[eg[i].v] |= 1 << eg[i].u;
}
for(int i = 0; i < n; ++ i){
bel[i] = bel[gf(i)];
}
be[0] = 1;
eg_cnt[0] = 0;
for(int S = 1; S < (1 << n); ++ S){
int x = 31 ^ __builtin_clz(S & -S);
be[S] = be[S^(S&sc[1<<x])] * ans[S&sc[1<<x]] % P;
new_sc[S] = new_sc[S^(S&bel[x])] | bel[x];
eg_cnt[S] = 0;
for(int i = l; i <= r; ++ i){
if(((S >> eg[i].u) & 1) && ((S >> eg[i].v) & 1)){
++ eg_cnt[S];
}
}
}
for(int i = 0; i < n; ++ i){
if(gf(i) == i && sc[1<<i] != new_sc[1<<i]){
for(int S = bel[i]; S; S = (S - 1) & bel[i]){
is[S] = 1;
}
}
}
//Part 1. 主旋律
memset(f, 0, sizeof(f));
memset(g, 0, sizeof(g));
for(int S = 1; S < (1 << n); ++ S){
if(!is[S]){
continue;
}
for(int T = (S - 1) & S; T; T = (T - 1) & S){
if((sc[S^T] & sc[T]) == 0 && (S & -S) == (T & -T)){
g[S] = (g[S] - f[T] * g[S^T] % P * ipw[E(sc[S^T],T)+E(sc[T],S^T)] % P + P) % P;
}
}
f[S] = 1;
for(int T = S; T; T = (T - 1) & S){
if((sc[S^T] & sc[T]) == 0){
f[S] = (f[S] - g[T] * ipw[E(sc[S^T],T)] % P + P) % P;
}
}
g[S] = (g[S] + f[S]) % P;
}
//Part 2. Others
for(int S = 1; S < (1 << n); ++ S){
if(!is[S]){
continue;
}
int cnt = 0;
for(int i = 0; i < n; ++ i){
if(new_sc[1<<i] == new_sc[S] && (sc[1<<i] & sc[S]) == 0){
cnt += __builtin_popcount(S & to[i]);
}
}
f[S] = f[S] * ipw[cnt] % P;
}
//Part 3. 转置
memset(dp, 0, sizeof(dp));
for(int S = 1; S < (1 << n); ++ S){
if(!is[S]){
continue;
}
int flg = 1;
for(int i = 0; i < n; ++ i){
if(new_sc[1<<i] == new_sc[S] && (sc[1<<i] & sc[S]) == 0){
flg = 0;
break;
}
}
dp[S] = flg;
}
for(int S = (1 << n) - 1; S; -- S){
if(!is[S]){
continue;
}
for(int T = (S - 1) & S; T; T = (T - 1) & S){
if((sc[S^T] & sc[T]) == 0){
dp[S^T] = (dp[S^T] + dp[S] * (P - ipw[E(sc[S^T], T)]) % P * be[T]) % P;
}
}
}
for(ll S = 1; S < (1 << n); ++ S){
if(dp[S]){
dp[S] = dp[S] * be[S] % P;
for(ll T = (S - 1) & S; T; T = (T - 1) & S){
if((sc[S^T] & sc[T]) == 0){
dp[T] = (dp[T] + dp[S]) % P;
}
}
}
}
for(int S = 1; S < (1 << n); ++ S){
if(!is[S]){
continue;
}
ans[S] = f[S] * dp[S] % P;
}
}
ll res = 0;
for(int S = 1; S < (1 << n); ++ S){
res = (res + ans[S]) % P;
}
printf("%lld\n", res);
return;
}
int main(){
pw[0] = ipw[0] = 1;
for(int i = 1; i < 1000; ++ i){
pw[i] = pw[i-1] * 2 % P;
ipw[i] = ipw[i-1] * i2 % P;
}
int c, T;
scanf("%d%d", &c, &T);
while(T--){
solve();
}
return 0;
}
9. P11118 [ROI 2024] 无人机比赛 (Day 2) (NOIP T4)
https://www.luogu.com.cn/problem/P11118。
题意:有一条赛道,每隔若干格有一个存档点,坐标分别是 \(s_1,s_2,...,s_m\)。\(n\) 个无人机进行比赛,第 \(i\) 个无人机飞 \(1\) 单位距离的时间是 \(t_i\)。每当一个无人机飞到一个存档点,它留在存档点,其他所有还未完赛的无人机全部返回到它最后一次存档的存档点(如果有多个无人机同时到达存档点,看作编号最小的到达其他的没有到达),定义一次返回存档点的操作为传送。一个无人机飞到存档点 \(m\) 即视为完赛,不参与后续的过程。对于每个 \(i\),求 \([1,i]\) 内的无人机进行比赛,整个过程中所有无人机在比赛结束之前一共将进行多少次传送。
\(n,m,s_m\leq 150000,t\leq 10^9\)。
设无人机 \(i\) 从存档点 \(j-1\) 飞到存档点 \(j\) 的时间为 \(w_{i,j}=t_i(s_j-s_{j-1})\),则操作序列相当于将这些 \(w\) 进行归并,每次选开头的最小的 \(w\) 放入队列中。
观察到如果 \(w_{i,j}\geq w_{i,j+1}\),则 \(w_{i,j+1}\) 一定紧跟在 \(w_{i,j}\) 之后,则直接合并即可。然后对于一个 \(i\),每一段开头的 \(w\) 值严格递增,于是每个 \(i\) 的 \(w\) 构成 \(\sqrt{s_m}\) 段。又发现 \(w\) 的大小关系和 \(i\) 无关,所以每一个 \(i\) 的分段都是相同的。
把操作序列每一步分别属于哪个无人机写出来,构成一个长度为 \(nm\),每个数出现 \(m\) 次的数列。计算这个数列对应的传送次数,我们可以发现等于 \(\sum_{i=1}^{nm}i[\forall j>i,col_i\neq col_j]-nm\),即找到每个无人机最后一次操作的下标累加起来再减去 \(nm\) 即可。
所以,对于那些不是最后一段的 \(w\),他们之间的大小关系是没有用的,只用关心 \(>\) 他们的最小 \(w_{*,m}\) 是什么即可。所以维护 \(n\) 个集合,每个集合表示小于某个 \(w_{*,m}\) 的操作段有哪些,然后遍历 \(i\in[1,n]\),将 \(w_{i,*}\) 插入对应集合中,然后激活 \(w_{i,m}\) 对应的集合(即这个集合的下标要计入答案),我们得到了一个正确的,看起来很好优化的做法。
问题 1:如何找到一个 \(w\) 对应的集合?对于段 \(p\),我们将 \(w_{i,p}\) 排序后双指针即可。复杂度 \(O(n\sqrt{s_m})\)。
问题 2:答案如何快速计算?我们会有 \(O(n\sqrt{s_m})\) 次集合大小的单点加,然后 \(n\) 次激活,每次激活查询一个前缀,使用 \(O(1)-O(\sqrt n)\) 分块。然后每次单点加的贡献是它后面的激活集合数,使用 \(O(\sqrt n)-O(1)\) 维护后缀激活集合数。
总复杂度 \(O(n\sqrt{s_m}+n\sqrt n)\)。
//P11118
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 150010, B = 550;
int n, m, t[N], s[N];
int mm, S[N], len[N];
pair<ll, int> bar[N];
int pos[N], hav[N];
int to[551][N];
int ind[N], le[N];
struct SQRT{
ll val[N], blv[N];
void add(int x, ll v){
val[x] += v;
blv[ind[x]] += v;
}
ll ask(int x){
ll ans = 0;
for(int i = 1; i < ind[x]; ++ i){
ans += blv[i];
}
for(int i = le[ind[x]]; i <= x; ++ i){
ans += val[i];
}
return ans;
}
} T1;
struct SQRT2{
int val[N], blv[N];
void add(int x, int v){
for(int i = 1; i < ind[x]; ++ i){
blv[i] += v;
}
for(int i = le[ind[x]]; i <= x; ++ i){
val[i] += v;
}
}
int ask(int x){
return val[x] + blv[ind[x]];
}
} T2;
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++ i){
scanf("%d", &t[i]);
ind[i] = (i - 1) / B + 1;
if(ind[i] != ind[i-1]){
le[ind[i]] = i;
}
}
for(int i = 1; i <= m; ++ i){
scanf("%d", &s[i]);
}
for(int i = m; i >= 1; -- i){
s[i] = s[i] - s[i-1];
}
for(int i = 1; i <= m; ++ i){
if(s[i] > S[mm]){
S[++mm] = s[i];
}
++ len[mm];
}
swap(mm, m);
for(int i = 1; i <= n; ++ i){
bar[i] = make_pair(1ll * t[i] * S[m], i);
}
sort(bar + 1, bar + n + 1);
for(int i = 1; i <= n; ++ i){
pos[bar[i].second] = i;
}
for(int i = 1; i < m; ++ i){
int pp = 1;
for(int j = 1; j <= n; ++ j){
ll val = bar[j].first / S[m];
int id = bar[j].second;
while(bar[pp] <= make_pair(1ll * val * S[i], id)){
++ pp;
}
to[i][id] = pp;
}
}
ll ans = 0;
for(int i = 1; i <= n; ++ i){
for(int j = 1; j < m; ++ j){
T1.add(to[j][i], len[j]);
ans += 1ll * len[j] * T2.ask(to[j][i]);
}
ans += 1ll * len[m] * T2.ask(pos[i]);
T1.add(pos[i], len[m]);
ans += T1.ask(pos[i]);
T2.add(pos[i], 1);
printf("%lld\n", ans - 1ll * mm * i);
}
return 0;
}
10. P5983 [PA 2019] Osady i warownie 2 (NOIP T4)
https://www.luogu.com.cn/problem/P5983。
题意:维护一个 \(n*m\) 的矩阵,初始所有地方都没有障碍,每次指定一个地方,求如果这个地方新增一个障碍,是否还存在一条 \((1,1)\to (n,m)\) 的只包含向右、向下的道路。如果还存在,这个地方增加一个障碍;否则不增加。强制在线。
\(n,m\leq 10^5,k\leq 10^6\)。
由于题目要求道路只能向右、向下,所以这个题和经典的对偶后连通性题目有区别。此题的维护方法是找最上、最下的两条路径。以维护最上路径为例:对于每一列,维护 \(r_i\) 表示这一列从 \((r_{i-1},i)\) 走到了 \((r_i,i)\),最下路径同。那么,如果一个点同时在最上、最下两条路径上,这个点一定会阻挡所有可行道路;否则不会。
现在的问题是,如果新增了一个点 \((x,y)\) 阻挡了一条路,不妨它阻挡了最上路径,我们需要找到一条新的最上路径。显然,我们需要从下方绕过点 \((x,y)\),即对于所有 \(i\in[y-1,m]\),将 \(r_i\) 与 \(x+1\) 取 \(\max\)。但是,此时这条路径不一定合法,对于第 \(y-1\) 列的 \((r_{y-1},r_y+1]\) 以及第 \(x+1\) 行的若干位置还没有考虑。假设我们找到了这些位置上的一个障碍,看做这个障碍在此处第一次添加,递归的求解即可。每个障碍只会添加一次,所以复杂度有保证。
如何找这些位置上的障碍?对于每一列维护一个小根堆、每一行维护一个大根堆,每次取堆顶,如果堆顶在最上路径上侧,不管他,如果找到一个在需考虑范围的障碍,考虑它即可。
一个实现的方式:最下路径可以看做翻转过后的最上路径,于是写一个 struct 维护最上路径,开两个这样的 struct 即可。
代码中使用分块维护 \(r\) 数组。复杂度 \(O(q\sqrt n)\)。
// Problem: P5983 [PA 2019] Osady i warownie 2
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5983
// Memory Limit: 512 MB
// Time Limit: 3000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
int n, m, IncimathCal, V;
const int N = 100010;
struct maintainer{
int tmp[55][55];
priority_queue<int, vector<int>, greater<int> > lie_min[N];
priority_queue<int> hang_max[N];
int r[N], inb[N], br[N], R[N];
const int B = 550;
void init(){
for(int i = 1; i <= m; ++ i){
r[i] = 1;
inb[i] = (i - 1) / B + 1;
if(inb[i] != inb[i-1]){
br[inb[i-1]] = i-1;
}
}
br[inb[m]] = m;
r[m] = n;
}
int getr(int x){
// return r[x];
if(x == 0) return 1;
// assert(r[x] >= R[inb[x]]);
return max(r[x], R[inb[x]]);
}
bool in(int x, int y){
// return r[y] >= x && r[y-1] <= x;
return getr(y) >= x && getr(y-1) <= x;
}
int cc = 0;
void add(int x, int y){
// if(getr(y-1) > x){
// return;
// }
// tmp[x][y] = 1;
if(!in(x, y)){
lie_min[y].push(x);
hang_max[x].push(y);
return;
}
lie_min[y].push(x);
hang_max[x].push(y);
// printf("add %d %d\n", x, y);
int le = max(1, y - 1);
++ cc;
// for(int i = le; i <= m; ++ i) r[i] = max(r[i], x + 1);
// printf("%d %d\n", le, br[inb[le]]);
// printf("%d %d\n",inb[le]+1, inb[m]);
for(int i = le; i <= br[inb[le]]; ++ i){
r[i] = max(getr(i), x + 1);
}
for(int i = inb[le] + 1; i <= inb[m]; ++ i){
if(getr(br[i]) <= x + 1){
R[i] = max(R[i], x + 1);
} else {
for(int j = br[i-1]+1; j <= br[i]; ++ j){
r[j] = max(getr(j), x + 1);
}
break;
}
}
while(lie_min[y-1].size()){
int px = lie_min[y-1].top();
// printf("lie %d %d %d\n", px, y-1, getr(y-1));
if(px < getr(y-2)){
// puts("123");
// if(px < r[y-1]){
lie_min[y-1].pop();
} else if(px <= x + 1){
lie_min[y-1].pop();
add(px, y-1);
} else {
break;
}
}
while(hang_max[x+1].size()){
int py = hang_max[x+1].top();
if(getr(py-1) > x+1){
// if(r[py-1] > x+1){
hang_max[x+1].pop();
} else if(py > y - 1){
hang_max[x+1].pop();
add(x+1, py);
} else {
break;
}
}
}
void chk(){
for(int p = 1; p <= n; ++ p){
for(int q = 1; q <= m; ++ q){
printf("%d", tmp[p][q]?tmp[p][q]:p>=r[q-1]&&p<=r[q]?3:0);
}
puts("");
}
for(int p = 1; p <= m; ++ p){
printf("%d ", r[p]);
}
for(int i = 1; i <= m; ++ i){
// // printf("%d %d\n", i, m);
for(int j = r[i-1]; j <= r[i]; ++ j){
if(tmp[j][i]){
// printf("%d %d %d\n", j, i, m);
// puts("");
// printf("%d\n", lie_min[49].top());
puts("WA");
exit(0);
}
}
}
}
} up, dn;
int main(){
scanf("%d%d%d", &n, &m, &IncimathCal);
up.init();
dn.init();
while(IncimathCal --){
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
x = (x ^ V) % n;
y = (y ^ V) % m;
++ x;
++ y;
if(up.in(x, y) && dn.in(n-x+1, m-y+1)){
puts("TAK");
// puts("Yes");
V ^= z;
} else {
puts("NIE");
// puts("No");
up.add(x, y);
dn.add(n-x+1, m-y+1);
// up.chk();
// dn.chk();
}
}
cerr << up.cc << ' ' << dn.cc << '\n';
return 0;
}
11. P5987 [PA 2019] Terytoria (NOIP T3)
https://www.luogu.com.cn/problem/P5987。
题意:在二维平面直角坐标系上,有一个长度为 \(X\),宽度为 \(Y\) 的地图,注意这个地图的左边界和右边界是连通的,下边界和上边界也是连通的。在这个地图里,有 \(X\times Y\) 个格子以及 \(n\) 个边平行坐标轴的矩形。你只知道每个矩形两个对顶点的坐标,请问在最好情况下,被所有 \(n\) 个矩形都覆盖住的格子数量有多少?
\(n\leq 5\times 10^5,2\leq X,Y\leq 10^9\)。
易证行列是完全独立的,那么考虑一行内,问题变为若干个区间,每个区间可以取它本身或者它的补,求一个方案使得被所有区间覆盖的长度最大。发现能被所有区间覆盖等价于,这些位置位于同一个区间覆盖的等价类中,异或哈希即可。
// Problem: P5987 [PA 2019] Terytoria
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5987
// Memory Limit: 256 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int n, W, H;
typedef unsigned long long ull;
vector<pair<int, ull> > a, b;
ull seed = 1238429304;
ull SR(){
seed = seed ^ (seed << 17);
seed = seed ^ (seed >> 13);
seed = seed ^ (seed << 5);
return seed;
}
map<ull, int> mx, my;
int ax, ay;
int main(){
scanf("%d%d%d", &n, &W, &H);
for(int i = 1; i <= n; ++ i){
int q, w, e, r;
scanf("%d%d%d%d", &q, &w, &e, &r);
ull t = SR();
a.emplace_back(q, t);
a.emplace_back(e, t);
b.emplace_back(w, t);
b.emplace_back(r, t);
}
a.emplace_back(0, 0);
a.emplace_back(W, 0);
b.emplace_back(0, 0);
b.emplace_back(H, 0);
sort(a.begin(), a.end());
sort(b.begin(), b.end());
ull tx = 0, ty = 0;
for(int i = 1; i <= n + n + 1; ++ i){
mx[tx] += a[i].first - a[i-1].first;
my[ty] += b[i].first - b[i-1].first;
ax = max(ax, mx[tx]);
ay = max(ay, my[ty]);
tx ^= a[i].second;
ty ^= b[i].second;
// printf("%llu %d\n", tx, a[i].first);
}
printf("%lld\n", 1ll * ax * ay);
return 0;
}
12. P5980 [PA 2019] Herbata (NOIP T2)
https://www.luogu.com.cn/problem/P5980。
题意:你有 \(n\) 个杯子,每个杯子里有温度为 \(a_i\),体积为 \(l_i\) 的水。你还有无限个无限容积的杯子,你可以进行无限次倒水,两杯水混合后体积相加,温度相加规律符合现实。求是否有方案使得每个杯子最后温度为 \(b_i\),输出有解或无解。
\(n\leq 10^5,l,a,b\leq 10^6\)。
有解条件:首先符合能量守恒;其次,将 \((l_i,a_i)\) 向量按照斜率从小到大首尾相连,\(b\) 的同理,\(b\) 所构成的凸包要非严格在 \(a\) 的凸包上面。
因为每次混合相当于两个向量相加,斜率差值只会减少不会增加。
// Problem: P5980 [PA 2019] Herbata
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5980
// Memory Limit: 125 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
typedef long long ll;
int T, n;
pair<ll, ll> a[N], b[N];
#define yes_ "TAK"
#define no_ "NIE"
int main(){
scanf("%d", &T);
while(T--){
ll sum = 0;
scanf("%d", &n);
for(int i = 1; i <= n; ++ i){
ll L, A, B;
scanf("%lld%lld%lld", &L, &A, &B);
a[i] = make_pair(A, L);
b[i] = make_pair(B, L);
sum += L * 1ll * (A - B);
}
sort(a + 1, a + n + 1);
sort(b + 1, b + n + 1);
if(sum){
puts(no_);
} else {
bool flg = 1;
int l = 1, r = 1;
sum = 0;
while(l <= n && r <= n){
if(a[l].second > b[r].second){
sum += 1ll * (a[l].first - b[r].first) * b[r].second;
a[l].second -= b[r].second;
++ r;
} else if(a[l].second < b[r].second){
sum += 1ll * (a[l].first - b[r].first) * a[l].second;
b[r].second -= a[l].second;
++ l;
} else {
sum += 1ll * (a[l].first - b[r].first) * a[l].second;
++ l;
++ r;
}
if(sum > 0){
flg = 0;
break;
}
}
puts(flg ? yes_ : no_);
}
}
return 0;
}
/*
244466
344555
*/
13. P10231 [COCI 2023/2024 #4] Putovanje (NOIP T2)
https://www.luogu.com.cn/problem/P10231。
题意:给你一张无向图,每个点有个值 \(d_i\),要么为自然数要么为 \(-1\),找到所有满足如下条件的点 \(x\):\(\forall i, dis(i,x)=d_i \operatorname{or} d_i=-1\),其中 \(dis\) 表示两点间最短路。
\(n\leq 5\times 10^4,m\leq 10^5\)。
太难了!
考虑,多源 bfs。每个点维护 \(dis_x=d_i-dis(i,x)\),以及满足这个式子的起点 \(i\) 集合(使用 bitset),每次更新 \(u\to v\),如果 \(dis_v=dis_u-1\) 或者 \(dis_v\) 未更新,则对应更新,否则 \(dis_v=dis_u\),不管他即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 50010;
int n, m;
vector<int> g[N];
bitset<N> b[N], all;
int d[N];
vector<int> ds[N];
int dis[N], vis[N], dd[N];
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; ++ i){
int u, v;
scanf("%d%d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
}
bool flg = 0;
int mx = 0;
for(int i = 1; i <= n; ++ i){
scanf("%d", &d[i]);
if(d[i] != -1){
flg = 1;
ds[d[i]].push_back(i);
mx = max(mx, d[i]);
all.set(i, 1);
}
}
if(!flg){
printf("%d\n", n);
for(int i = 1; i <= n; ++ i){
printf("%d ", i);
}
puts("");
} else {
int flg = 1;
int cnt = 0;
memset(dis, 0xcf, sizeof(dis));
queue<int> q;
for(int i : ds[mx]){
dis[i] = mx;
q.push(i);
b[i].set(i, 1);
vis[i] = 1;
}
ds[mx].clear();
while(!q.empty()){
int x = q.front();
q.pop();
if(!dis[x] || dd[x]){
continue;
}
dd[x] = 1;
for(auto i : ds[dis[x]-1]){
if(vis[i] && dis[i] != d[i]){
flg = 0;
}
q.push(i);
vis[i] = 1;
if(dis[i] == d[i]){
b[i] |= b[x];
b[i].set(i, 1);
} else {
b[i].set(i, 1);
dis[i] = d[i];
}
}
ds[dis[x]-1].clear();
for(auto i : g[x]){
if(dis[i] <= dis[x] - 1){
b[i] |= b[x];
dis[i] = dis[x] - 1;
q.push(i);
vis[i] = 1;
}
}
}
for(int i = 1; i <= n; ++ i){
if(flg&&dis[i] == 0 && b[i] == all){
++ cnt;
}
}
printf("%d\n", cnt);
for(int i = 1; i <= n; ++ i){
if(flg&&dis[i] == 0 && b[i] == all){
printf("%d ", i);
}
}
// printf("[%d %d]", b[107].count);
puts("");
}
return 0;
}
14. P13626 [ICPC 2024 APC] XOR Operations
https://www.luogu.com.cn/problem/P13626。
题意:给定序列 \(a\) 和初始为 \(0\) 的序列 \(b\)。每次可以操作 \((i,j)\) 使得 \(b_i,b_j\) 都异或上 \(a_i\operatorname{XOR} a_j\)。求最后能到达的 \(b\) 序列数量。
\(n\leq 200000,a_i\leq 2^{30}-1\)。
容易发现:对于一对 \((i,j)\),操作 \(0\) 次和操作 \(2\) 次是相同的,我们只用考虑它操作了 \(0\) 或 \(1\) 次。所以我们可以建图:对于一组操作方案,如果操作了 \((i,j)\),则连无向边 \((i,j)\),否则不连。
这样得到了 \(2^{\frac{n(n-1)}2}\) 张图,而显然其中部分图虽然方案不同,但最后的结果是相同的。而如果图 \(G\) 和图 \(H\) 的结果相同,求出它们的边集对称差 \(P\)(对称差即在且仅在 \(G,H\) 其一出现的边构成的集合),那么图 \(P\) 对应的结果应该为 \(\forall i, b_i=0\)。
这启发我们找所有操作过后 \(b\) 全 \(0\) 的图 \(P\)。首先不管整个图,考虑图上一个点 \(i\),\(b_i\) 的取值会由偶数个 \(a\) 异或而得。那么,如果我们找到了一个集合 \(S\),使得 \(\{a_i|i\in S\}\) 张成的线性空间等于 \(\{a\}\) 张成的线性空间,且 \(S\) 是最小的代表元集合之一,那么此时,如果我们随意连 \(U/S\) 内的边,然后再决定这些点中的每一个,要不要使用 \(S\) 内点改变它连边数奇偶性,这样 \(S/x\) 内有唯一一种连边方式使得构成的图对应结果为全 \(0\)!具体的,我们给 \(S\) 内部点定一个顺序,然后每个点都只有一种连边方案,即可证明。
所以我们要找 \(|S|\),即所有偶数大小集合构成的线性基大小。我们令 \(a_i\leftarrow 2a_i+1\),然后跑线性基即可。
那么,所有图,每个等价类里都有 \(2^{\frac{(n-|S|)(n-|S|+1)}2}\) 张图(即上述连边方案数),最后的答案就是 \(2^{\frac{n(n-1)}2}\div 2^{\frac{(n-|S|)(n-|S|+1)}2}\)。
//P13626
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, a[N];
int p[30], cnt;
void ins(int x){
for(int i = 30; i >= 0; -- i){
if(!(x & (1 << i))){
continue;
}
if(!p[i]){
p[i] = x;
return;
}
x ^= p[i];
}
++ cnt;
}
const long long P = 998244353;
long long qp(long long x, long long y){
long long ans = 1;
while(y){
if(y & 1){
ans = ans * x % P;
}
x = x * x % P;
y >>= 1;
}
return ans;
}
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; ++ i){
scanf("%d", &a[i]);
a[i] = 2 * a[i] + 1;
ins(a[i]);
}
long long ans = qp(2, 1ll * n * (n - 1) / 2);
long long div = qp((P + 1) / 2, 1ll * cnt * (cnt + 1) / 2);
printf("%lld\n", ans * div % P);
return 0;
}
15. P13826 [Ynoi Easy Round 2026] 寒蝉鸣泣之时
https://www.luogu.com.cn/problem/P13826。
题意:给定 \(n\) 个边平行于坐标轴的平面矩形,以及正整数 \(m\geq \sqrt n\),对 \(1≤m\times i≤n\) 的每个整数 \(i\) ,你需要计算出恰好被 \(m\times i\) 个矩形包含的区域的面积。
\(n\leq 3\times 10^5\)。
首先是一些套路操作:沿一维扫描线,然后每次操作相当于,区间 \(+1/-1\),查询整体有多少个位置的值为 \(m\) 的倍数。考虑分块,把序列分为 \(B\) 块。
我们单独考虑一块 \([l,r]\),这一块是散块修改和整块修改交替操作的。而每次修改过后,这个块都要对答案贡献一次。本题的核心想法在于:每次修改过后贡献到答案太浪费,只在散块修改之前贡献答案。
具体的,如果第 \(a_1,a_2,...,a_k\) 次操作是散块修改,我们在 \(a_1\) 处计算 \([1,a_1)\) 这些操作后的贡献;在 \(a_2\) 处计算 \([a_1,a_2)\) 这些操作后的贡献,等等,最后计算 \([a_k,2n)\) 这些操作的贡献(转换为扫描线后共有 \(2n\) 次操作)。这样的优点是,每个 \([a_i,a_{i+1})\) 区间内,操作都是整块修改,所以块内元素两两的差值不变,变的只有块整体的一个偏移量。
现在我们要计算一段操作区间的贡献。设 \(0,p_1,p_2,...,p_k\) 是每次修改后的偏移量,\(l_0,l_1,...,l_k\) 是两次修改之间被拍成时间轴的那一维的长度。那么对于我们分块维护的序列的第 \(i\) 项,它的值为 \(i+0,i+p_1,i+p_2,...,i+p_k\),每个值的维持时间是 \(l\) 中的某一项。我们暴力地去找 \(m|i+p_j\) 的数量。由于 \(p\) 数组一定是值域连续的一段(每次变化量为 \(0/1\)),所以 \(\max\{p\}-\min\{p\}\leq k\),我们可以找到那 \(O(\dfrac km)\) 个可以贡献的 \(p_j\) 的值,这样的话,每块重构复杂度是 \(O(\dfrac km\sqrt n)\)。所有的 \(k\) 的和是 \(O(n\sqrt n)\) 的,所以总复杂度 \(O(\dfrac{n^2}m)=O(n\sqrt n)\)。
16. P10209 [JOI 2024 Final] 路网服务 2 / Road Service 2
https://www.luogu.com.cn/problem/P10209。
题意:给你一个 \(n\times m\) 的网格图,每条无向边连接 \((i,j),(i+1,j)\) 或者 \((i,j),(i,j+1)\)。你可以花费 \(c_i\in\{1,2\}\) 的代价将所有 \(i\) 行上的边建出来。\(Q\) 次询问,每次询问给你若干点,求使得这些点联通的最小代价。
\(nm\leq 10^6,\sum |S|\leq 2\times 10^5\)。
首先可以发现,一个连通块可以看作一个区间。因为,建边只能在一行内建且一下子建完一行内所有边。所以每次建边操作相当于将所有能够到达某一行的连通块全部连起来。这样的话,求出每个连通块最上、最下能够到达哪一行,就可以转化为一个区间上的问题:给定若干个区间,选择一个位置可以使得这个位置上的区间全部连通,多次询问求一个区间集合最小连通代价。
还是不够好!我们考虑,将选择的位置集合提取出来,设为 \(S\)。那么,对于询问区间集合内的每一个区间 \([l,r]\),\(S\cup [l,r]\) 不能为空;且对于 \(S\) 内相邻的两个元素 \(i,j\),要有一个区间 \(i,j\in [l',r']\)。那么题目转化为找到这么一个代价最小的 \(S\) 集合。
\(c_i=1,|S|=2\)
设两个区间分别为 \([l,r]\) 和 \([L,R]\)(\(l\leq r<L\leq R\))。我们从小往大考虑哪些位置应该放入 \(S\) 中。首先,为了使得后面的限制更宽松,我们应该将 \(r\) 放到 \(S\) 中。接下来,我们容易预处理一个数组 \(rch_i\) 表示 \(i\) 往右侧最右边到哪个点,使得存在一个区间覆盖这个点和 \(i\),那么接下来就应该选 \(rch_i\),一直这么做下去,直到找到一个 \(p\) 使得 \(rch_p\geq L\),这样就可以选择 \(L\) 了。
所以,我们所选择的点是 \(r,rch_r,rch_{rch_r},...\),发现是一个倍增的形式,预处理 \(jmp_{j,x}\) 表示 \(x\) 开始跳 \(2^j\) 次到哪即可。
\(c_i=1\)
此时,询问区间集合内的区间不只有两个,将这些区间按照右端点排序为 \([l_1,r_1],[l_2,r_2],...,[l_k,r_k]\)。我们对于 \([l_1,r_1],[l_2,r_2]\) 跑上述算法,将这两个区间连通。但是要有一个修改:结尾虽然是可以选择 \(l_2\),但是并不是最优的,最优的是 \(\min(rch_p,r_2)\),因为这个更靠右。然后从这个开始为起点,继续倍增,对于 \([l_2,r_2],[l_3,r_3]\) 跑上述算法,直到跑到 \([l_k,r_k]\) 使得所有区间连通即可。
正解
此时 \(c\) 可以取到 \(2\),很多性质就不正确了,例如,开始的点并不一定是 \(l_1\) 最优,等等。
考虑 dp。设 \(dp_i\) 以及一个 \(st\) 表示,我们选择了代价和为 \(i\) 的区间,连通了 \([l_i,r_i],[l_{st},r_{st}]\),最后一个选择的点最大能到哪。转移是 \(rch_{dp_i}\to dp_{i+2}\)(或者 \(\min(rch_{dp_i},r_k)\to dp_{i+2}\);定义 \(la1_i\) 表示 \(i\) 前 \(c=1\) 的第一个位置,\(la1_{rch_{dp_i}}\to dp_{i+1}\)(或者 \(la1_{\min(r_k,rch_{dp_i})}\to dp_{i+1}\))。
其实也是可以倍增优化的。先不管区间的限制,考虑设 \(jmp_{j,i,0/1}\) 表示从 \(i\) 开始跳 \(2^j-1/2^j\) 步能够到哪。初始是 \(jmp_{0,i,0}=i,jmp_{0,i,1}=la1_{rch_i}\)。转移:
第一个转移的后半段不能省略,因为前半段的方案中,\(2^{j-1},2^{j-1}+1\) 这两个代价是一定不在一次跳跃中的,而后者是一定在一次跳跃中的。
然后,大体思路是,对于两个分开很远的区间,倍增跳过去;对于两个叠起来的区间,分类讨论地转移。
具体的转移步骤(目前的 \(ans\) 表示 \(s2=dp_{ans},s1=dp_{ans-1}\) ):
-
初始化 \(s1=la1_{r_1}\),如果 \(dp_1<l_1\) 则设为不存在;\(s2=r_1\)(注意,此时这个值不一定是真正的 \(dp_2\) 的值,因为 \(dp_2\) 可以从 \(dp_1\) 转移而来),目前的 \(ans=2\);如果 \(c_{r_1}=1\),则 \(s2=r_1,s1=0\),目前的 \(ans=1\)。
-
枚举 \(i=\{2,3,...,k\}\),执行以下 \(3\sim 6\) 操作。每次操作结束后保证 \(s2\in[l_i,r_i]\),因此 \(s1\) 不一定 \(\in[l_i,r_i]\),转移的时候需要着重考虑。
-
如果 \(s1\notin[l_{i-1},r_{i-1}]\)。考虑 \(s1\) 在 \([l_{i-1},r_{i-1}]\) 内跳两步,\(s2\) 在 \([l_i,r_i]\) 内跳一步,设为 \(s3\)。如果 \(s3<s2\),则 \(s1\leftarrow 0\) 表示不考虑;否则令 \(\{s1,s2\}\leftarrow\{s2,s3\}\)。注意,此处的 \(s2\) 可能并不是真正的 \(s2\),因为上文中“\(s2\) 在 \([l_i,r_i]\) 内跳一步”,并不是可能的最优情况。
-
处理一下 1 处产生的漏洞:\(s2\) 值并不真正正确,用 \(s1\) 在 \([l_i,r_i]\) 内跳一步更新 \(s2\)。
-
如果 \(s2\) 已经在 \([l_i,r_i]\) 内。如果 \(s1\) 也在,直接不管;如果 \(s1\) 不在且 \(rch_{s1}>l_i\)(可以更新),那么仿照 3 更新 \(s1\),以及产生一个可能并非正确的 \(s2\);如果不能更新,直接扔掉 \(s1\)(置为 \(0\))。
-
否则,倍增跳到使得 \(s2\) 是 \([l_i,r_i]\) 前的最后一个状态,然后分讨 \(s3\) 存不存在,使用 \(s3\) 或者 \(s3,s4\) 更新 \(s1,s2\)。
最后,答案取 \(s1\) 或者 \(s2\)。
//P10209
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int n, m, Q;
char red[N];
vector<int> A[N], B[N], vis[N];
int C[N];
int tot, mn[N], mx[N];
void dfs(int x, int y, int col){
queue<pair<int, int> > q;
vis[x][y] = col;
q.push(make_pair(x, y));
while(!q.empty()){
x = q.front().first, y = q.front().second;
mn[col] = min(mn[col], x);
mx[col] = max(mx[col], x);
q.pop();
if(x < n && !vis[x+1][y] && B[x][y]){
q.push(make_pair(x + 1, y));
vis[x+1][y] = col;
}
if(y < m && !vis[x][y+1] && A[x][y]){
q.push(make_pair(x, y + 1));
vis[x][y+1] = col;
}
if(x > 1 && !vis[x-1][y] && B[x-1][y]){
q.push(make_pair(x - 1, y));
vis[x-1][y] = col;
}
if(y > 1 && !vis[x][y-1] && A[x][y-1]){
q.push(make_pair(x, y - 1));
vis[x][y-1] = col;
}
}
}
int rch[N], hb[N], la1[N];
bool cmp(int x, int y){
return mx[x] != mx[y] ? mx[x] < mx[y] : mn[x] > mn[y];
}
int jmp[22][N][2];
int main(){
scanf("%d%d%d", &n, &m, &Q);
for(int i = 1; i <= n; ++ i){
A[i].resize(m + 1);
vis[i].resize(m + 1);
scanf("%s", red + 1);
for(int j = 1; j < m; ++ j){
A[i][j] = red[j] - '0';
}
}
for(int i = 1; i < n; ++ i){
B[i].resize(m + 1);
scanf("%s", red + 1);
for(int j = 1; j <= m; ++ j){
B[i][j] = red[j] - '0';
}
}
for(int i = 1; i <= n; ++ i){
scanf("%d", &C[i]);
rch[i] = i;
}
for(int i = 1; i <= n; ++ i){
for(int j = 1; j <= m; ++ j){
if(!vis[i][j]){
++ tot;
mn[tot] = n;
dfs(i, j, tot);
rch[mn[tot]] = max(rch[mn[tot]], mx[tot]);
}
}
}
for(int i = 2; i <= n; ++ i){
rch[i] = max(rch[i], rch[i-1]);
}
int tcc = 0;
for(int i = 1; i <= n; ++ i){
hb[i] = tcc;
if(rch[i] == i){
++ tcc;
}
la1[i] = la1[i-1];
if(C[i] == 1){
la1[i] = i;
}
jmp[0][i][0] = i;
}
for(int i = 1; i <= n; ++ i){
jmp[0][i][1] = la1[rch[i]] >= i ? la1[rch[i]] : 0;
}
for(int j = 1; j < 22; ++ j){
for(int i = 1; i <= n; ++ i){
jmp[j][i][1] = max(jmp[j-1][jmp[j-1][i][1]][1], jmp[j-1][rch[jmp[j-1][i][0]]][0]);
jmp[j][i][0] = max(jmp[j-1][jmp[j-1][i][1]][0], jmp[j-1][jmp[j-1][i][0]][1]);
}
}
for(int cs = 1; cs <= Q; ++ cs){
int T, x, y;
scanf("%d", &T);
vector<int> v;
map<int, int> mp;
for(int i = 1; i <= T; ++ i){
scanf("%d%d", &x, &y);
if(!mp[vis[x][y]]){
mp[vis[x][y]] = 1;
v.push_back(vis[x][y]);
}
}
sort(v.begin(), v.end(), cmp);
if(v.size() == 1){
puts("0");
} else if(hb[mx[v[0]]] != hb[mx[v[v.size()-1]]]){
puts("-1");
} else {
int ans, s2, s1;
if(C[mx[v[0]]] == 1){
s2 = mx[v[0]];
s1 = 0;
ans = 1;
} else {
s2 = mx[v[0]];
s1 = la1[mx[v[0]]];
ans = 2;
}
for(int i = 1; i < v.size(); ++ i){
if(s1 < mn[v[i-1]]){
int s3 = max(min(mx[v[i-1]], rch[s1]), la1[min(mx[v[i]], rch[s2])]);
if(s3 < s2){
s1 = 0;
} else {
s1 = s2;
s2 = s3;
++ ans;
}
}
if(la1[min(mx[v[i]], rch[s1])] > s2){
s2 = la1[min(mx[v[i]], rch[s1])];
}
if(s2 >= mn[v[i]]){
if(s1 < mn[v[i]] && rch[s1] > mn[v[i]]){
int s3 = max(min(mx[v[i]], rch[s1]), la1[min(mx[v[i]], rch[s2])]);
s1 = s2;
s2 = s3;
++ ans;
} else if(s1 < mn[v[i]]){
s1 = 0;
}
} else {
for(int j = 21; j >= 0; -- j){
int ns2 = max(jmp[j][s2][1], jmp[j][rch[s1]][0]);
if(ns2 < mn[v[i]]){
s1 = max(jmp[j][s1][1], jmp[j][s2][0]);
s2 = ns2;
ans += 1 << j;
}
}
int s3 = max(min(mx[v[i]], rch[s1]), la1[min(mx[v[i]], rch[s2])]);
int s4 = max(min(mx[v[i]], rch[s2]), la1[min(mx[v[i]], rch[s3])]);
if(s3 >= mn[v[i]] && s3 > s2){
s1 = s2;
s2 = s3;
++ ans;
} else {
s1 = s3;
s2 = s4;
ans += 2;
}
}
}
if(s1 >= mn[v[v.size()-1]]){
-- ans;
}
printf("%d\n", ans);
}
}
return 0;
}
17. P10211 [CTS2024] 线段树
https://www.luogu.com.cn/problem/P10211。
给一棵广义线段树,以及 \(m\) 个询问区间 \([l,r]\)。线段树上每个点的值你可能知道,可能不知道,总共 \(2^{2n-1}\) 种情况。求有多少种情况,这 \(m\) 个询问区间的值是都知道的。
\(n,m\leq 2\times 10^5\)。
考虑建 \(n+1\) 个点的一张图。对于线段树上某个点表示的区间 \([l,r]\),如果这个点的值知道,那么连边 \(l\leftrightarrow r+1\),否则不管。那么,一个区间 \([L,R]\) 能够得到值,相当于 \(L,R+1\) 连通。
特殊性质:要求全图连通。那么,由线段树的分治结构,每部分有两种情况:子树内连通/不连通,分别用 \(f,g\) 表示,则转移:
- \(f_p\leftarrow 2f_{ls}f_{rs}+f_{ls}g_{rs}+g_{ls}f_{rs}\)(两边都连通整体随便接/只有一边连通,整体必须接)
- \(g_p\leftarrow f_{ls}g_{rs}+g_{ls}f_{rs}\)(只有一边连通)
原问题与之的区别是,不要求全图连通。考虑一个点 \(p\) 代表区间 \([L,R]\),连接 \(l=L,r=R+1\),那么所有询问区间与其有三种情况:被 \(p\) 包含;与 \(p\) 相交;包含 \(p\) 或与 \(p\) 不交。对于第一种,这些区间会对 \(p\) 的转移产生限制;第二种,我们需要维护这些区间端点与 \(l,r+1\) 的连通性,然后放到后面处理;第三种,在此处先不用管。称第二类点为关键点。
一个性质:对于点 \(l,r\),中间有若干关键点,这些关键点显然要和 \(l,r\) 其一连通,否则一定是不合法的。我们其实可以发现,一定是一个前缀和 \(l\) 连通,一个后缀和 \(r\) 连通,因为如果不满足,那么它们一定有交点,从而这两个点与 \(l,r\) 都连通。
那么我们就可以设 \(g_{p,x}\) 表示 \([l,x]\) 内的关键点连 \(l\);其他关键点连 \(r\) 的方案数。\(f\) 一样是 \([l,r]\) 连通的方案数(并不意味着所有点连通!)。转移:
- \(f_p\leftarrow 2f_{ls}f_{rs}\),没有影响;
- \(f_p\leftarrow f_{ls}g_{rs,*}+f_{rs}g_{ls,*}\),表示连整体,不全连一侧的两端通过另一侧连起来;
- \(g_{p,x}\leftarrow f_{ls}g_{rs,x}+f_{rs}g_{ls,x}\),表示不连整体。
- \(g_{p,x}\leftarrow g_{ls,x}g_{rs,y},f_{p}\leftarrow g_{ls,x}g_{rs,y}\),此时有一些在 \(ls,rs\) 内为关键点的点就会有限制了:这个转移相当于舍弃了 \([x+1,y]\) 这个区间内的所有点不和外界连通,所以对于一个 \(a,b\) 连通的要求,显然这两者不能其一在 \([x+1,y]\) 内,就是 \([a,b]\) 与 \([x+1,y]\) 不交或包含。我们在此处考虑所有区间 \([a,b]\),如果有一个不合法,那么这个显然是不行的;如果都合法,那么在此处舍弃 \([x+1,y]\) 不会影响后面的转移。
考虑 xor hashing,令 \(hash_{[a,b-1]}\) 都异或上一个随机权值,那么,如果 \(hash_x=hash_y\),就可以转移,否则不行。
那么把 \(g_{p,x}\) 的定义转化为 \(g_{p,hash_x}\),然后离散化一下,转移变成形如 \(g_{p,x}=g_{ls,x}g_{rs,x}\) 的形式,使用线段树合并即可。
//P10211
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int n, m;
typedef unsigned long long ull;
ull ha[N], sr = 10000727, pool[N];
int id[N];
ull rnd(){
sr = sr ^ (sr << 13);
sr = sr ^ (sr >> 5);
sr = sr ^ (sr << 17);
return sr;
}
int tot = 1;
struct sgtree{
int ls, rs, l, r;
} tt[N];
void build(int p, int l, int r){
if(l == r){
tt[p].l = l;
tt[p].r = r + 1;
} else {
int mid;
scanf("%d", &mid);
tt[p].ls = ++ tot;
tt[p].rs = ++ tot;
build(tt[p].ls, l, mid);
build(tt[p].rs, mid+1, r);
tt[p].l = tt[tt[p].ls].l;
tt[p].r = tt[tt[p].rs].r;
}
}
typedef long long ll;
const ll P = 998244353;
ll f[N], g[5010][5010];
int le[N], ri[N];
struct node{
int ls, rs;
ll sum, tag;
} t[N*30];
int rt[N], cnt;
void psd(int p){
if(t[p].ls && t[p].tag != 1){
t[t[p].ls].sum = t[t[p].ls].sum * t[p].tag % P;
t[t[p].ls].tag = t[t[p].ls].tag * t[p].tag % P;
}
if(t[p].rs && t[p].tag != 1){
t[t[p].rs].sum = t[t[p].rs].sum * t[p].tag % P;
t[t[p].rs].tag = t[t[p].rs].tag * t[p].tag % P;
}
t[p].tag = 1;
}
void add(int &p, int l, int r, int x, int v){
if(!p){
p = ++ cnt;
t[p].tag = 1;
}
if(l == r){
t[p].sum = v;
} else {
int mid = l + r >> 1;
psd(p);
if(x <= mid){
add(t[p].ls, l, mid, x, v);
} else {
add(t[p].rs, mid+1, r, x, v);
}
t[p].sum = (t[t[p].ls].sum + t[t[p].rs].sum) % P;
}
}
ll qry(int p, int l, int r, int ql, int qr){
if(!p || qr < l || r < ql){
return 0;
} else if(ql <= l && r <= qr){
return t[p].sum;
} else {
int mid = l + r >> 1;
psd(p);
return (qry(t[p].ls, l, mid, ql, qr) + qry(t[p].rs, mid+1, r, ql, qr)) % P;
}
}
ll ss = 0;
void mg(int &p, int q, int l, int r, ll A, ll B){
if(!p && !q){
return;
} else if(!p){
p = q;
t[p].sum = t[p].sum * B % P;
t[p].tag = t[p].tag * B % P;
} else if(!q){
t[p].sum = t[p].sum * A % P;
t[p].tag = t[p].tag * A % P;
} else if(l == r){
ss = (ss + t[p].sum * t[q].sum) % P;
t[p].sum = (A * t[p].sum % P + B * t[q].sum % P + t[p].sum * t[q].sum % P) % P;
} else {
int mid = l + r >> 1;
psd(p);
psd(q);
mg(t[p].ls, t[q].ls, l, mid, A, B);
mg(t[p].rs, t[q].rs, mid+1, r, A, B);
t[p].sum = (t[t[p].ls].sum + t[t[p].rs].sum) % P;
}
}
int main(){
scanf("%d%d", &n, &m);
build(1, 1, n);
for(int i = 1; i <= m; ++ i){
int l, r;
scanf("%d%d", &l, &r);
++ l;
ull val = rnd();
ha[l] ^= val;
ha[r+1] ^= val;
le[i] = l;
ri[i] = r + 1;
}
for(int i = 1; i <= n + 1; ++ i){
ha[i] ^= ha[i-1];
pool[i] = ha[i];
}
sort(pool + 1, pool + n + 2);
m = unique(pool + 1, pool + n + 2) - pool - 1;
for(int i = 1; i <= n + 1; ++ i){
id[i] = lower_bound(pool + 1, pool + m + 1, ha[i]) - pool;
}
for(int i = tot; i >= 1; -- i){
if(tt[i].l + 1 == tt[i].r){
f[i] = 1;
add(rt[i], 1, m, id[tt[i].l], 1);
} else {
int ls = tt[i].ls, rs = tt[i].rs;
ss = 0;
f[i] = (f[ls] * f[rs] * 2 % P + f[ls] * t[rt[rs]].sum % P + t[rt[ls]].sum * f[rs] % P) % P;
mg(rt[ls], rt[rs], 1, m, f[rs], f[ls]);
rt[i] = rt[ls];
f[i] = (f[i] + ss) % P;
}
}
printf("%lld\n", (f[1] + qry(rt[1], 1, m, id[n+1], id[n+1])) % P);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号