做题笔记 01
1. CF2031F Penchick and Even Medians [*2800]
https://www.luogu.com.cn/problem/CF2031F。
题意:交互题。初始有一个长度为偶数的序列,每次可以给出大小为偶数且 \(\geq 4\) 的一个下标集合,表示询问一个子序列,返回这个子序列中两个中位数的数值。需要求出原序列中两个中位数的位置。
\(n\leq 100\),询问次数 \(\leq 80\)。
设 \(L=n/2, R=n/2+1\),考虑问一个长度为 \(n-2\) 的子序列会有什么效果:
- 返回 \(L,R\),表示删去的这两个下标中没有中位数。
- 返回 \(L,R+1\) 或者 \(L-1,R\),表示删去的这两个下标中有一个中位数 \(R\) 或 \(L\)。
- 返回 \(L-1, R+1\),表示删去的两个下标就是两个中位数,直接得到答案。
- 返回 \(L-1, L\),表示删去了两个 \(\geq R\) 的数,可能存在中位数。
- 返回 \(R, R+1\),表示删去了两个 \(\leq L\) 的数,可能存在中位数。
问题在于最后两种返回值,不能得到很有效的信息。
观察到前三种返回值都代表着这两个数不同时位于 \([1,L],[R,n]\) 之间,而后两种返回值能够确定这两个数位于哪个区间之内,这就意味着后两种返回值出现次数是相同的。
那么两两匹配后两种返回值,设删去 \(i,i+1\) 是第四种情况,删去 \(j,j+1\) 是第五种情况,那么询问 \(i,i+1,j,j+1\):
- 若返回 \(L,R\),则表示这四个下标中有两个中位数。
- 若返回值中有 \(L\),说明下标 \(j,j+1\) 中有一个中位数 \(L\)。
- 若返回值中有 \(R\),说明下标 \(i,i+1\) 中有一个中位数 \(R\)。
- 否则这四个下标中都没有中位数。
那么现在要么直接得到了答案,要么通过第一次分讨的情况 3 以及第二次分讨的情况 2,3 得到了两组数 \((a,b),(c,d)\),表示下标 \(a,b\) 中,下标 \(c,d\) 中分别有一个中位数,四种情况都可以删去对应下标查看返回值是否为 \(L-1,R+1\) 来进行检查。
总的询问次数是 \(n/2+n/4+4=50+25+4=79<80\)。
//CF2031F
#include <cstdio>
#include <algorithm>
#include <utility>
using namespace std;
int T, n;
pair<int, int> ask4(int a, int b, int c, int d){
printf("? 4 %d %d %d %d\n", a, b, c, d);
fflush(stdout);
int x, y;
scanf("%d%d", &x, &y);
if(x > y){
swap(x, y);
}
return make_pair(x, y);
}
pair<int, int> askp2(int a, int b){
printf("? %d ", n - 2);
for(int i = 1; i <= n; ++ i){
if(i != a && i != b){
printf("%d ", i);
}
}
puts("");
fflush(stdout);
int x, y;
scanf("%d%d", &x, &y);
if(x > y){
swap(x, y);
}
return make_pair(x, y);
}
void ans(int x, int y){
printf("! %d %d\n", x, y);
fflush(stdout);
}
int up[110], dn[110];
void solve(){
int L = n / 2, R = n / 2 + 1;
int aa = 0, bb = 0, cc = 0, dd = 0;
int tp = 0, tq = 0;
for(int i = 1; i <= n; i += 2){
pair<int, int> x = askp2(i, i+1);
if(x.first == L - 1 && x.second == R + 1){
ans(i, i+1);
return;
} else if(x.first == L ^ x.second == R){
if(!aa){
aa = i;
bb = i + 1;
} else {
cc = i;
dd = i + 1;
}
} else if(x.second == L){
++ tp;
up[tp] = i;
} else if(x.first == R){
++ tq;
dn[tq] = i;
}
}
for(int i = 1; i <= tp; ++ i){
pair<int, int> x = ask4(up[i], up[i]+1, dn[i], dn[i]+1);
if(x.first == L && x.second == R){
aa = up[i];
bb = up[i] + 1;
cc = dn[i];
dd = dn[i] + 1;
} else if(x.first == L){
if(!aa){
aa = dn[i];
bb = dn[i] + 1;
} else {
cc = dn[i];
dd = dn[i] + 1;
}
} else if(x.second == R){
if(!aa){
aa = up[i];
bb = up[i] + 1;
} else {
cc = up[i];
dd = up[i] + 1;
}
}
}
if(askp2(aa, cc) == make_pair(L - 1, R + 1)){
ans(aa, cc);
return;
}
if(askp2(aa, dd) == make_pair(L - 1, R + 1)){
ans(aa, dd);
return;
}
if(askp2(bb, cc) == make_pair(L - 1, R + 1)){
ans(bb, cc);
return;
}
if(askp2(bb, dd) == make_pair(L - 1, R + 1)){
ans(bb, dd);
return;
}
}
int main(){
scanf("%d", &T);
while(T--){
scanf("%d", &n);
solve();
}
return 0;
}
2. AT_abc400_g [ABC400G] Patisserie ABC 3 [*2813]
https://www.luogu.com.cn/problem/AT_abc400_g。
题意:给定 \(n\) 个三元组 \((a_i,b_i,c_i)\),两个三元组 \(i,j\) 匹配的价值是 \(\max(a_i+a_j,b_i+b_j,c_i+c_j)\),求一个大小为 \(k\) 的匹配使得价值最大。
\(n\leq 10^5, a,b,c\leq 10^9\)。
一个观察:价值虽然是三维的 \(\max\),但是实际上可以看做选定一维,因为这样不会使得答案更大,且能够取到那个最优答案。
那么这个形式变成了:对于每个下标,可以不选或者选 \(a,b,c\) 其中一个。最终要选 \(a,b,c\) 分别偶数个,且选择 \(2k\) 个数,要求使得总和最大。
忽略选择 \(2k\) 个数的限制,是可以直接 dp 的。设 \(f_{i,S}\) 表示考虑前 \(i\) 个三元组,\(a,b,c\) 选择的奇偶性情况为 \(S\) 即可。
考虑选择 \(2k\) 个数的限制,容易想到 wqs 二分。由于关于选择的数个数的函数在偶数下标上是上凸的(显然),有结论:
上凸 \(f\) 求 \(f(a)\),可以求下凸函数 \(g(k) = \max(f(x) - k*x) + k*a\) 的最小值。
证明:https://www.cnblogs.com/KiharaTouma/p/18758564/Corruption#16cf739e---gosha-is-hunting。
有细节,就是 f(x) 实际上选择了 \(2x\) 个数(即 \(x\) 对数),在算 \(f(x)-kx\) 的时候要注意一下。
// Problem: G - Patisserie ABC 3
// Contest: AtCoder - AtCoder Beginner Contest 400
// URL: https://atcoder.jp/contests/abc400/tasks/abc400_g
// Memory Limit: 1024 MB
// Time Limit: 3000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int T, n, K, a[N], b[N], c[N];
typedef long long ll;
ll f[N][8];
//上凸 f 求 f(a),可以求 g(k) = max(f(x) - k*x) + k*a 的最小值
ll chk(ll k){
memset(f[0], 0xcf, sizeof(f[0]));
f[0][0] = 0;
for(int i = 1; i <= n; ++ i){
memset(f[i], 0xcf, sizeof(f[i]));
for(int j = 0; j < 8; ++ j){
f[i][j] = max(f[i][j], f[i-1][j]);
f[i][j^1] = max(f[i][j^1], f[i-1][j] + a[i] - k);
f[i][j^2] = max(f[i][j^2], f[i-1][j] + b[i] - k);
f[i][j^4] = max(f[i][j^4], f[i-1][j] + c[i] - k);
}
}
return f[n][0] + 1ll * k * K;
}
int main(){
scanf("%d", &T);
while(T--){
scanf("%d%d", &n, &K);
K *= 2;
for(int i = 1; i <= n; ++ i){
scanf("%d%d%d", &a[i], &b[i], &c[i]);
a[i] *= 2;
b[i] *= 2;
c[i] *= 2;
}
ll L = 0, R = 3e9;
while(L + 5 < R){
ll mid = L + R >> 1;
if(chk(mid) < chk(mid + 1)){
R = mid + 1;
} else {
L = mid;
}
}
ll ans = 1e18;
for(int i = L; i <= R; ++ i){
ans = min(ans, chk(i));
}
printf("%lld\n", ans / 2);
}
return 0;
}
3. AT_arc101_d [ARC101F] Robots and Exits [*2930]
https://www.luogu.com.cn/problem/AT_arc101_d。
题意:数轴上有 \(n\) 个机器人和 \(m\) 个出口,坐标两两不同。每次可以选择所有机器人向左或向右走一步,如果机器人和出口坐标相同,则机器人从这个出口出去。求有多少种机器人-出口的完美匹配使得存在一种操作序列,可以使得每个机器人都能从与其匹配的出口出去。
\(n,m\leq 10^5\)。
对于一个操作序列,我们显然可以用一个二元组 \((a,b)\) 表示一段前缀的操作情况:表示一个坐标为 \(x\) 的机器人在这段前缀中走到了 \([x-a,x+b]\) 内的所有坐标上;那么接下来的操作就可以转换为 \(a\leftarrow a+1\) 或者 \(b\leftarrow b+1\)。
对于一个机器人,设它距离左右两侧出口分别为 \(x,y\),如果从左侧走,那么要求是操作中第一次 \(a\geq x\) 的项早于第一次 \(b\geq y\) 的项,反之同理。对于那些在所有出口左边或者所有出口右边的机器人,不管他们即可。
那么问题转化为,有若干二元组 \((x_i,y_i)\),要求有多少种每个二元组选 \(x\) 或者 \(y\) 的方案使得能够找到一组合法的操作序列二元组。
把每个限制都画在坐标系上,相当于找到一条从 \((0,0)\) 出发的折线,每个限制在折线哪一侧就相当于这个机器人走哪一边的出口。为了去重,可以强制折线上所有右拐的地方,那个右下方的格子都有限制。所以一个合法方案对应着一个限制集合,其中这个集合两两完全偏序。
将限制二元组按照 \(x\) 排序,设 \(f_i\) 表示选定第 \(i\) 个二元组选 \(y\),前 \(i\) 个二元组都考虑好的方案数。转移是:
答案是 \(\sum f\),使用树状数组优化即可。
//AT_arc101_d
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
const int P = 1e9 + 7;
int n, m, a[N], b[N], c;
pair<int, int> p[N];
int f[N];
int buc[N], bc;
int bit[N];
void add(int p, int v){
while(p <= bc){
bit[p] = (bit[p] + v) % P;
p += p & -p;
}
}
int ask(int p){
int rs = 0;
while(p){
rs = (rs + bit[p]) % P;
p -= p & -p;
}
return rs;
}
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++ i){
scanf("%d", &a[i]);
}
for(int i = 1; i <= m; ++ i){
scanf("%d", &b[i]);
}
b[m+1] = 2e9;
int r = 1;
for(int i = 1; i <= n; ++ i){
while(b[r] < a[i]){
++ r;
}
if(r != m + 1 && r != 1){
p[++c] = make_pair(a[i] - b[r-1], b[r] - a[i]);
buc[c] = b[r] - a[i];
}
}
sort(buc + 1, buc + c + 1);
bc = unique(buc + 1, buc + c + 1) - buc - 1;
sort(p + 1, p + c + 1);
c = unique(p + 1, p + c + 1) - p - 1;
int ans = 1;
for(int i = 1, l = 0; i <= c; ++ i){
p[i].second = lower_bound(buc + 1, buc + bc + 1, p[i].second) - buc;
if(p[i].first != p[i-1].first){
for(int j = l + 1; j < i; ++ j){
add(p[j].second, f[j]);
}
l = i - 1;
}
f[i] = (1 + ask(p[i].second - 1)) % P;
ans = (ans + f[i]) % P;
}
printf("%d\n", ans);
return 0;
}
4. P7230 [COCI 2015/2016 #3] NEKAMELEONI [紫]
https://www.luogu.com.cn/problem/P7230。
题意:给定一个序列,单点修改,查询最短子串使得子串中出现过值域 \(k\) 内所有正整数,输出长度。
\(n,q,k\leq 10^5\),原题 \(k\leq 50\)。
考虑对于每个 \(i\) 维护 \(R_i\) 表示 \(i,R_i\) 是可行区间。设 \(r_{c,i}\) 表示 \(i\) 后面第一个 \(c\) 出现的位置,则 \(R_i=\max_c\{r_{c,i}\}\)。修改序列会改变 \(r_{c,i}\)。具体的,删除一个位置的数是 \(r_{c,i}\) 一段区间改为更大的值;添加一个位置的数是 \(r_{c,i}\) 一段区间改为更小的值。显然前者和 \(R\) 的方向相同,更好维护。于是考虑线段树分治转化为只删除,那么每次删除一个数相当于一段 \(R\) 的 chkmax,由于单调性可以直接 cover 维护。为了支持撤销,使用主席树维护即可。
注意实现,主席树 pushdown 肯定是要补全子结点或者新建子结点备份的。由于要线段树二分,需要递归到叶子,此时若对于不存在 tag 的点 pushdown 的同时依旧补全子结点空间就完蛋了。对于这个题线段树二分到了一个空点那么直接跳过是对的。
//P7230
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, m, k, a[N], la[N], ask[N];
struct fff{
int col, pos, st, ed;
};
vector<fff> v;
multiset<int> occ[N];
vector<pair<int, int> > del[N*4];
void add(int p, int l, int r, pair<int, int> v, int ql, int qr){
if(qr < l || r < ql){
return;
} else if(ql <= l && r <= qr){
del[p].push_back(v);
} else {
int mid = l + r >> 1;
add(p<<1, l, mid, v, ql, qr);
add(p<<1|1, mid+1, r, v, ql, qr);
}
}
int tp;
struct node{
int ls, rs, tag, mn, val;
} t[N*130];
int rt[N*90], cnt = 1;
int rrcnt[N*90];
void psd(int p, int l, int r){
if(t[p].tag){
t[++cnt] = t[t[p].ls];
t[p].ls = cnt;
t[++cnt] = t[t[p].rs];
t[p].rs = cnt;
int mid = l + r >> 1;
t[t[p].ls].tag = t[t[p].ls].val = t[p].tag;
t[t[p].rs].tag = t[t[p].rs].val = t[p].tag;
t[t[p].ls].mn = t[p].tag - mid + 1;
t[t[p].rs].mn = t[p].tag - r + 1;
t[p].tag = 0;
}
}
void mdf(int &p, int l, int r, int ql, int qr, int v){
if(qr < l || r < ql) return;
t[++cnt] = t[p];
p = cnt;
if(ql <= l && r <= qr){
t[p].tag = v;
t[p].val = v;
t[p].mn = v - r + 1;
} else {
int mid = l + r >> 1;
psd(p, l, r);
if(ql <= mid){
mdf(t[p].ls, l, mid, ql, qr, v);
}
if(mid < qr){
mdf(t[p].rs, mid+1, r, ql, qr, v);
}
t[p].mn = min(t[t[p].ls].mn, t[t[p].rs].mn);
t[p].val = max(t[t[p].ls].val, t[t[p].rs].val);
}
}
int getmx(int &p, int l, int r, int ql, int qr, int v){
if(t[p].val < v){
return qr + 1;
} else if(l == r){
return l;
} else {
t[++cnt] = t[p];
p = cnt;
int mid = l + r >> 1;
psd(p, l, r);
if(qr <= mid){
return getmx(t[p].ls, l, mid, ql, qr, v);
} else if(mid < ql){
return getmx(t[p].rs, mid+1, r, ql, qr, v);
} else {
if(t[t[p].ls].val > v){
return getmx(t[p].ls, l, mid, ql, qr, v);
}
return getmx(t[p].rs, mid+1, r, ql, qr, v);
}
}
}
void chkmx(int &p, int l, int r, int val){
if(l > r) return;
int L = getmx(p, 1, n, l, r, val);
mdf(p, 1, n, l, L-1, val);
}
void dfs(int p, int l, int r){
for(auto i : del[p]){
int pos = i.first, col = i.second;
occ[col].erase(occ[col].lower_bound(pos));
if(occ[col].find(pos) == occ[col].end()){
auto it = occ[col].lower_bound(pos);
int R = *it;
-- it;
int L = *it;
rrcnt[tp] = cnt;
++ tp;
rt[tp] = rt[tp-1];
chkmx(rt[tp], L+1, pos, R);
}
}
if(l == r){
if(ask[l]){
ask[l] = t[rt[tp]].mn;
if(ask[l] > n){
ask[l] = -1;
}
}
} else {
int mid = l + r >> 1;
dfs(p<<1, l, mid);
dfs(p<<1|1, mid+1, r);
}
reverse(del[p].begin(), del[p].end());
for(auto i : del[p]){
int pos = i.first, col = i.second;
if(occ[col].find(pos) == occ[col].end()){
-- tp;
cnt = rrcnt[tp];
}
occ[col].insert(pos);
}
}
int main(){
scanf("%d%d%d", &n, &k, &m);
for(int i = 1; i <= n; ++ i){
scanf("%d", &a[i]);
}
for(int i = 1; i <= m; ++ i){
int op, p, vv;
scanf("%d", &op);
if(op == 1){
scanf("%d%d", &p, &vv);
v.push_back({a[p], p, la[p], i-1});
a[p] = vv;
la[p] = i;
} else {
ask[i] = 1;
}
}
for(int i = 1; i <= n; ++ i){
v.push_back({a[i], i, la[i], m});
}
for(auto i : v){
occ[i.col].insert(i.pos);
add(1, 0, m, make_pair(i.pos, i.col), 0, i.st - 1);
add(1, 0, m, make_pair(i.pos, i.col), i.ed + 1, m);
}
t[0].mn = 2e9;
rt[0] = 1;
for(int i = 1; i <= k; ++ i){
occ[i].insert(0);
occ[i].insert(1e9);
int la = 0;
for(auto it : occ[i]){
chkmx(rt[0], la+1, n, it);
la = it;
}
}
dfs(1, 0, m);
for(int i = 1; i <= m; ++ i){
if(ask[i]){
printf("%d\n", ask[i]);
}
}
return 0;
}
5. P10438 [JOIST 2024] 塔楼 / Tower [紫]
https://www.luogu.com.cn/problem/P10438。
题意:一个 \([0,+\inf]\) 数轴,有 \(n\) 段不交区间 \([l_i,r_i]\) 是障碍,每次可以花费 \(A\) 的时间从 \(i\) 走路到 \(i+1\);或者 \(B\) 的时间从 \(i\) 跳跃到 \(i+D\)(前提是起点终点都不是障碍)。\(q\) 次询问,每次给定 \(x\) 问从 \(0\) 走到 \(x\) 的最短时间。
\(n,q\leq 10^5, l_i,r_i,D\leq 10^{12}\)。
发现 \(A*D\) 与 \(B\) 的大小关系是一个重点。
Part 1. \(A*D\leq B\)
此时走路一定更优。设 \(f_i\) 表示从 \(0\) 走到 \(i\) 的最优方案下的跳跃次数。\(n\) 个障碍将数轴分为了 \(n+1\) 段,考虑每一段的 \(f\) 取值,容易发现先是一段 \(f\) 不可行,再是一段相同的 \(f\)。计算这个分割点位置可以通过二分解决:设目前这一段为 \([l_i,r_i]\),二分不小于 \(l_i-D\) 的最小可行位置,设之为 \(x\),若 \(x+D\leq r_i\),从这个位置跳跃一步转移到 \(f_{x+D}\),同时 \(x+D\) 为这一段的分割点。
那么我们求得了所有可行段(\(\leq n+1\) 段,有的段可能完全不可行),以及每一段对应的 \(f\),容易二分求答案。
Part 2. \(A*D>B\)
这一部分比较复杂。依旧考虑先求所有可行段,那么此时每一段内的 \(f\) 不再是相同的,而是如下结构:先是一段 \(f=x\),长度 \(\leq D\),后面每 \(D\) 格 \(f\) 值 \(+1\):
- \(f_{[l_i,l_i+k_i]}=x\);
- \(f_{[l_i+k_i+1,l_i+k_i+D]}=x+1\);
- \(f_{[l_i+k_i+D+1,l_i+k_i+D+D]}=x+2\);
- 。。。
那么为了求解答案,我们应该计算出这个 \(k\) 的取值。
考虑二分,首先从 \(f_{l_i-D}\) 转移到 \(f_{l_i}\),那么 \(l_i+k_i\) 这个位置应该是最后一个 \(f\) 取值等于 \(f_{l_i}\) 的位置,二分即可。注意 \(l_i+k_i-D\) 不一定是个合法位置,此时应该由这个位置左侧的第一个合法位置转移过来(代表着在前面的一个位置先跳,然后再在 \(i\) 这一段内走)。
此处形如一个二分套二分,复杂度 \(O(n\log^2 n)\)。
// Problem: P10438 [JOIST 2024] 塔楼 / Tower
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P10438
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 200010;
const ll inf = 2e18;
int n, m, Q;
ll D, A, B, l[N], r[N];
struct line{
ll l, r;
} a[N], b[N];
int cnt[N];
namespace solve1{
ll qry(ll x){
int L = 1, R = m, ans = m + 1;
while(L <= R){
int mid = L + R >> 1;
if(b[mid].r >= x){
ans = mid;
R = mid - 1;
} else {
L = mid + 1;
}
}
if(ans == m + 1 || b[ans].l > x){
return -1;
}
return (x - cnt[ans] * D) * A + cnt[ans] * B;
}
int main(){
while(Q--){
ll x;
scanf("%lld", &x);
printf("%lld\n", qry(x));
}
return 0;
}
}
namespace solve2{
ll f[N], pos[N];
ll ask(ll x){
int l = 1, r = m, ans = m + 1;
while(l <= r){
int mid = l + r >> 1;
if(b[mid].r >= x){
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
if(ans == m + 1 || b[ans].l > x){
x = b[--ans].r;
}
return f[ans] +
(x - b[ans].l) / D +
((x - b[ans].l) % D >= pos[ans] ? 1 : 0);
}
ll qry(ll x){
int l = 1, r = m, ans = m + 1;
while(l <= r){
int mid = l + r >> 1;
if(b[mid].r >= x){
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
if(ans == m + 1 || b[ans].l > x){
return -1;
}
return f[ans] +
(x - b[ans].l) / D +
((x - b[ans].l) % D >= pos[ans] ? 1 : 0);
}
int main(){
f[1] = 0;
pos[1] = D;
for(int i = 2; i <= m; ++ i){
f[i] = ask(b[i].l - D) + 1;
ll l = b[i].l, r = min(b[i].r, b[i].l + D - 1);
pos[i] = D;
while(l <= r){
ll mid = l + r >> 1;
if(ask(mid - D) == f[i]){
pos[i] = mid - b[i].l;
r = mid - 1;
} else {
l = mid + 1;
}
}
}
while(Q--){
ll x;
scanf("%lld", &x);
ll v = qry(x);
printf("%lld\n", v == -1 ? -1 : x * A + (B - A * D) * v);
}
return 0;
}
}
int main(){
scanf("%d%d%lld%lld%lld", &n, &Q, &D, &A, &B);
for(int i = 1; i <= n; ++ i){
scanf("%lld%lld", &l[i], &r[i]);
}
l[n+1] = inf;
a[1] = {0, l[1] - 1};
for(int i = 1; i <= n; ++ i){
a[i+1] = {r[i] + 1, l[i+1] - 1};
}
b[1] = a[1];
m = 1;
for(int i = 1, j = 1; i <= n + 1; ++ i){
while(j <= m && b[j].r + D < a[i].l){
++ j;
}
if(j <= m && b[j].l + D <= a[i].r){
++ m;
b[m] = {
max(b[j].l + D, a[i].l),
a[i].r
};
cnt[m] = cnt[j] + 1;
}
}
if(D * A <= B){
solve1::main();
} else {
solve2::main();
}
}
6. P9676 [ICPC 2022 Jinan R] Skills [紫]
https://www.luogu.com.cn/problem/P9676。
题意:有三种技能,在第 \(i\) 天学习第 \(j\) 种技能可以使得这个技能的熟练度增加 \(a_{i,j}\),对于其他两个技能,若这是第 \(k\) 天没学这个技能,熟练度 \(-k\) 并与 \(0\) 取 \(\max\)。求 \(n\) 天后三个技能熟练度的和的最大值。
\(n\leq 1000,a_{i,j}\leq 10000\)。
一道动态规划题,需要发现两个并不是很显然的性质,然后就可以做了。
性质 1:每个技能一旦学习了就不会让他的熟练度再变为 \(0\)。
显然,如果不满足,可以将前面那些白学习的天用来学习别的技能。这个性质的用处是可以将学习分为三个阶段:学习了 \(1/2/3\) 种技能,然后分段 dp 就可以不考虑每个技能的熟练度与 \(0\) 取 \(\max\) 的部分了,因为如果一个技能的熟练度减到了负数一定不优,且一定能够转移到一个最优解。
第一段是简单的:前缀和即可。
第二段,设 \(f_{i,0/1/2,0/1/2,x}\) 表示考虑到第 \(i\) 天,第 \(i\) 天选择的是第 \(0/1/2\) 个技能,另外一个学习过的技能是 \(0/1/2\),这个技能已经连续 \(x\) 天没有学了。转移分两种:从 \(f_{i-1}\) 的转移以及从第一段转移。
第三段,设 \(f_{i,0/1/2,x,y}\) 表示考虑到第 \(i\) 天,第 \(i\) 天选择的是第 \(0/1/2\) 个技能,另外两个技能分别连续 \(x,y\) 天没有学了。转移同样分两种。
性质 2:一个技能,若学习过,不可能连续大约 \(2\sqrt a_i\) 天未学习。
这么多天的未学习不一定会使得这个技能的熟练度变为负数,但是若调整一下,在这一段时间的中间抽出一天学习一下这个技能,那么这个技能熟练度的减少量会显著减少(显然可以挽回 \(>\max\{a_i\}\) 的损失,更优)
于是第三段 dp 的 \(x,y\) 只有 \(O(\sqrt{a_i})\),总复杂度 \(O(n\max\{a_i\})\)。
//P9676
#include <bits/stdc++.h>
using namespace std;
int T, n, a[3][1010], sum[3][1010];
int f[2][3][225][225], g[2][3][3][225];
int main(){
scanf("%d", &T);
while(T--){
memset(f, 0xcf, sizeof(f));
memset(g, 0xcf, sizeof(g));
scanf("%d", &n);
for(int i = 1; i <= n; ++ i){
scanf("%d%d%d", &a[0][i], &a[1][i], &a[2][i]);
sum[0][i] = sum[0][i-1] + a[0][i];
sum[1][i] = sum[1][i-1] + a[1][i];
sum[2][i] = sum[2][i-1] + a[2][i];
}
for(int i = 1; i <= n; ++ i){
memcpy(f[0], f[1], sizeof(f[1]));
memset(f[1], 0xcf, sizeof(f[1]));
memcpy(g[0], g[1], sizeof(g[1]));
memset(g[1], 0xcf, sizeof(g[1]));
for(int p = 0; p < 3; ++ p){
for(int q = 0; q < 3; ++ q){
if(p == q){
continue;
}
g[1][p][q][1] = a[p][i] + sum[q][i-1] - 1;
for(int x = 1; x <= min(n, 220); ++ x){
g[1][p][q][1] = max(g[1][p][q][1], g[0][q][p][x] + a[p][i] - 1);
if(x > 1){
g[1][p][q][x] = g[0][p][q][x-1] + a[p][i] - x;
}
}
}
}
for(int x = 1; x <= min(n, 220); ++ x){
for(int y = 1; y <= min(n, 220); ++ y){
if(x > 1 && y > 1){
f[1][0][x][y] = f[0][0][x-1][y-1] + a[0][i] - x - y;
f[1][1][x][y] = f[0][1][x-1][y-1] + a[1][i] - x - y;
f[1][2][x][y] = f[0][2][x-1][y-1] + a[2][i] - x - y;
}
f[1][0][1][y+1] = max(f[1][0][1][y+1], f[0][1][x][y] + a[0][i] - 1 - y - 1);
f[1][2][x+1][1] = max(f[1][2][x+1][1], f[0][1][x][y] + a[2][i] - 1 - x - 1);
f[1][1][1][y+1] = max(f[1][1][1][y+1], f[0][0][x][y] + a[1][i] - 1 - y - 1);
f[1][2][1][x+1] = max(f[1][2][1][x+1], f[0][0][x][y] + a[2][i] - 1 - x - 1);
f[1][0][y+1][1] = max(f[1][0][y+1][1], f[0][2][x][y] + a[0][i] - 1 - y - 1);
f[1][1][x+1][1] = max(f[1][1][x+1][1], f[0][2][x][y] + a[1][i] - 1 - x - 1);
}
f[1][0][1][x+1] = max(f[1][0][1][x+1], g[0][1][2][x] + a[0][i] - 1 - x - 1);
f[1][0][x+1][1] = max(f[1][0][x+1][1], g[0][2][1][x] + a[0][i] - 1 - x - 1);
f[1][1][1][x+1] = max(f[1][1][1][x+1], g[0][0][2][x] + a[1][i] - 1 - x - 1);
f[1][1][x+1][1] = max(f[1][1][x+1][1], g[0][2][0][x] + a[1][i] - 1 - x - 1);
f[1][2][1][x+1] = max(f[1][2][1][x+1], g[0][0][1][x] + a[2][i] - 1 - x - 1);
f[1][2][x+1][1] = max(f[1][2][x+1][1], g[0][1][0][x] + a[2][i] - 1 - x - 1);
}
}
int ans = max({sum[0][n], sum[1][n], sum[2][n]});
for(int p = 0; p < 3; ++ p){
for(int x = 1; x <= min(n, 220); ++ x){
for(int q = 0; q < 3; ++ q){
ans = max(ans, g[1][p][q][x]);
}
for(int y = 1; y <= min(n, 220); ++ y){
ans = max(ans, f[1][p][x][y]);
}
}
}
printf("%d\n", ans);
}
return 0;
}
\(\color{red}{\texttt{hard}}\) 7. P6556 The Forest [紫]
https://www.luogu.com.cn/problem/P6556。
题意:给你两棵树,问有多少个点集在第一棵树上连通,在第二棵树上是一条链。
\(n\leq 10^5\)。
点边容斥:树上点导出子图连通块数=点数-两端都在点集中的边数。
证明显然,想到这一点也不难,但是难点在于怎么去用它。
考虑第二棵树是链的情况,相当于一个序列,求多少个子区间在树上是连通的。扫描线,扫到点 \(r\),对于所有 \(l\),维护 \(t_{[l,r]}\) 表示区间 \([l,r]\) 的点集在第一棵树上的 \(|V|-|E|\)。每次加入一个 \(r\) 相当于对 \([1,r]\) 区间 \(+1\),以及对所有第一棵树上的边 \((x,r)\),若 \(x<r\) 则将 \([1,x]\) 区间 \(-1\)。用线段树维护,答案是每次线段树上 \(1\) 的个数,而由定义 \(1\) 是线段树上最小值,所以可以通过维护线段树上最小值个数来求解。
第二棵树不是链的情况,考虑通过换根维护同样的事情:目前根为 \(r\),线段树上第 \(i\) 个叶子表示第二棵树上 \(i\to r\) 路径的 \(|V|-|E|\),考虑换根的过程,假设根从 \(u\) 换到了 \(v\),\(T_x\) 表示以目前根的 \(x\) 子树点集:
- (目前根为 \(u\))要让 \(T_v\) 里所有点到根路径去掉点 \(u\),全体 \(-1\) 表示少了一个点;
- (目前根为 \(u\))要让 \(T_v\) 里所有点到根路径去掉点 \(u\),对于所有第一棵树上的边 \((u,x),x\in T_v\),\(T_x\) 内所有点 \(+1\),表示少了一条边;
- 将根变为 \(v\),不用操作;
- (目前根为 \(v\))要让 \(T_u\) 里所有点到根路径加上点 \(v\),全体 \(+1\) 表示多了一个点;
- (目前根为 \(u\))要让 \(T_u\) 里所有点到根路径加上点 \(v\),对于所有第一棵树上的边 \((v,x),x\in T_u\),\(T_x\) 内所有点 \(-1\),表示多了一条边。(注意此处类比换根树剖,需要分类讨论 \(x\) 的位置来确定 \(T_x\) 到底是哪个集合)。
对于最初始的情况,dfs 一遍先计算就可以。
注意到这么做的复杂度是正确的:每条边只会加入删除 \(O(1)\) 次,复杂度容易假的地方在于操作 \(2\) 该如何找到那些边,对于第一棵树上的边 \((u,v)\) 把他绑定到点 \(u\) 上,然后对于 \(v\) 在第二棵树上的 dfn 序排序,这样的话每次 \(2\) 操作需要的边是一段区间,直接维护一个指针即可。
//P6556
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int T, n;
vector<int> ag[N], g[N];
int dfn[N], dfc, val[N], anc[N], siz[N];
bool cmp(int x, int y){
return dfn[x] < dfn[y];
}
long long ans;
void dfs(int x, int fa){
anc[x] = 1;
siz[x] = 1;
dfn[x] = ++ dfc;
val[dfn[x]] = val[dfn[fa]] + 1;
for(int i : ag[x]){
if(anc[i]){
-- val[dfn[x]];
}
}
for(int i : g[x]){
if(i == fa){
continue;
}
dfs(i, x);
siz[x] += siz[i];
}
anc[x] = 0;
}
int t[N*4], mnc[N*4], tag[N*4];
void build(int p, int l, int r){
tag[p] = 0;
if(l == r){
t[p] = val[l];
mnc[p] = 1;
} else {
int mid = l + r >> 1;
build(p<<1, l, mid);
build(p<<1|1, mid+1, r);
if(t[p<<1] == t[p<<1|1]){
t[p] = t[p<<1];
mnc[p] = mnc[p<<1] + mnc[p<<1|1];
} else if(t[p<<1] < t[p<<1|1]){
t[p] = t[p<<1];
mnc[p] = mnc[p<<1];
} else {
t[p] = t[p<<1|1];
mnc[p] = mnc[p<<1|1];
}
}
}
struct opt{
int l, r, v;
};
stack<opt> st;
void psd(int p){
if(tag[p]){
tag[p<<1] += tag[p];
tag[p<<1|1] += tag[p];
t[p<<1] += tag[p];
t[p<<1|1] += tag[p];
tag[p] = 0;
}
}
void add(int p, int l, int r, int ql, int qr, int v, bool is = 1){
if(p == 1 && is){
st.push({ql, qr, v});
}
if(qr < l || r < ql){
return;
} else if(ql <= l && r <= qr){
tag[p] += v;
t[p] += v;
} else {
int mid = l + r >> 1;
psd(p);
add(p<<1, l, mid, ql, qr, v);
add(p<<1|1, mid+1, r, ql, qr, v);
if(t[p<<1] == t[p<<1|1]){
t[p] = t[p<<1];
mnc[p] = mnc[p<<1] + mnc[p<<1|1];
} else if(t[p<<1] < t[p<<1|1]){
t[p] = t[p<<1];
mnc[p] = mnc[p<<1];
} else {
t[p] = t[p<<1|1];
mnc[p] = mnc[p<<1|1];
}
}
}
int son[N];
void huangen(int x, int fa){
int tp = 0;
son[fa] = x;
anc[x] = 1;
ans += mnc[1];
for(int i : g[x]){
if(i == fa){
continue;
}
int sz = st.size();
son[x] = i;
while(tp < ag[x].size()){
if(dfn[ag[x][tp]] >= dfn[i] + siz[i]){
break;
}
if(dfn[ag[x][tp]] >= dfn[i]){
add(1, 1, n, dfn[ag[x][tp]], dfn[ag[x][tp]] + siz[ag[x][tp]] - 1, 1);
}
++ tp;
}
add(1, 1, n, dfn[i], dfn[i] + siz[i] - 1, -1);
for(int j : ag[i]){
if(dfn[j] >= dfn[i] && dfn[j] < dfn[i] + siz[i]){
} else if(anc[j]){
add(1, 1, n, 1, dfn[son[j]] - 1, -1);
add(1, 1, n, dfn[son[j]] + siz[son[j]], n, -1);
} else {
add(1, 1, n, dfn[j], dfn[j] + siz[j] - 1, -1);
}
}
add(1, 1, n, 1, dfn[i] - 1, 1);
add(1, 1, n, dfn[i] + siz[i], n, 1);
huangen(i, x);
while(st.size() > sz){
add(1, 1, n, st.top().l, st.top().r, - st.top().v, 0);
st.pop();
}
}
anc[x] = 0;
son[fa] = 0;
}
int main(){
scanf("%d", &T);
while(T--){
scanf("%d", &n);
for(int i = 1; i < n; ++ i){
int u, v;
scanf("%d%d", &u, &v);
ag[u].push_back(v);
ag[v].push_back(u);
}
for(int i = 1; i < n; ++ i){
int u, v;
scanf("%d%d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
}
dfs(n, 0);
build(1, 1, n);
ans = 0;
for(int i = 1; i <= n; ++ i){
sort(ag[i].begin(), ag[i].end(), cmp);
}
huangen(n, 0);
printf("%lld\n", (ans + n) / 2);
dfc = 0;
for(int i = 1; i <= n; ++ i){
vector<int> ().swap(g[i]);
vector<int> ().swap(ag[i]);
}
}
return 0;
}
\(\color{red}\texttt{hard}\) 8. P6667 [清华集训 2016] 如何优雅地求和
https://www.luogu.com.cn/problem/P6667。
题意:给定 \(m\) 次多项式 \(f\) 在 \([0,m]\) 的取值 \(a_0,a_1,...,a_m\),求 \(Q(f,n,x)=\sum_{k=0}^{n}f(k)\binom nkx^k(1−x)^{n−k}\)。
\(n\leq 10^9,m\leq 20000\)。
trick:类似的前缀和状物式子,将 \(f\) 用下降幂表示可能优于用普通幂表示。(或者可以尝试 \(\dbinom xi\))
设 \(f(x)=\sum_{i=0}^m b_ix^{\underline i}\),则有 \(a_k=f(k)=\sum_{i=0}^m b_ik^{\underline i}=\sum_{i=0}^k b_ii!\dbinom ki\)。
二项式反演得 \(b_kk!=\sum_{i=0}^k\dbinom ki (-1)^{k-i}a_i\),即 \(b_k=\sum_{i=0}^k\dfrac{a_i(-1)^{k-i}}{i!(k-i)!}\)。
带入原式,目标是计算出每个 \(a\) 的系数:
设 \(g(j)=\sum_{i=0}^{m-j} (-x)^i\dbinom{n-j}i\),有:
可以递推。
//P6667
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 20010;
const ll P = 998244353;
int n, m;
ll x, a[N], g[N], inv[N];
ll qp(ll x, ll y){
ll ans = 1;
while(y){
if(y & 1){
ans = ans * x % P;
}
x = x * x % P;
y >>= 1;
}
return ans;
}
int main(){
scanf("%d%d%lld", &n, &m, &x);
for(int i = 0; i <= m; ++ i){
scanf("%lld", &a[i]);
}
inv[1] = 1;
for(int i = 2; i <= m + 1; ++ i){
inv[i] = P - (P / i) * inv[P%i] % P;
}
g[m] = 1;
ll val = 1, Cnj = 1;
for(int i = m-1; i >= 0; -- i){
Cnj = Cnj * (n - i - 1) % P * inv[m-i] % P;
val = val * (P - x) % P;
g[i] = (1 - x + P) % P * g[i+1] % P;
g[i] = (g[i] + val * Cnj) % P;
}
ll ans = 0;
val = Cnj = 1;
for(int i = 0; i <= m; ++ i){
ans = (ans + a[i] * val % P * Cnj % P * g[i]) % P;
val = val * x % P;
Cnj = Cnj * (n - i) % P * inv[i+1] % P;
}
printf("%lld\n", ans);
return 0;
}
更多:将多项式从下降幂改成组合数,形式会更好看,甚至不用递推。
9. \(\color{red}\texttt{hard}\) P8421 [THUPC 2022 决赛] rsraogps
https://www.luogu.com.cn/problem/P8421。
题意:给定序列 \(a,b,c\),定义一个区间 \([l,r]\) 的权值为 \(a_{[l,r]}\) 按位与,\(b_{[l,r]}\) 按位或,\(c_{[l,r]}\) 的 \(\gcd\) 三个数的乘积。多次询问 \(l,r\),求所有 \([l,r]\) 的子区间的权值和。
\(n\leq 10^6,q\leq 5\times 10^6\)。
考虑扫描线,扫到 \(r\) 时维护 \(A_i,B_i,C_i\) 表示区间 \([i,r]\) 对应运算的答案,\(s_i\) 表示左端点在 \([1,i]\) 内,右端点在 \([1,r]\) 内的区间的权值和(相当于 \(A_kB_kC_k(k\leq i)\) 的历史和,虽然这道题并不需要用到历史和),那么询问 \([l,r]\) 的答案可以拆分为扫到 \(r\) 时的 \(s_r-s_{l-1}\)。
一个并不是很显然的结论是:扫描线 \(r\to r+1\),\(A_iB_iC_i\) 的值只有一段 \([r-p,r]\) 会改变,然后这个 \(p\) 的大小是均摊 \(O(\log V)\) 的。具体证明可以考虑拆位,每一位会在什么时候改变这个乘积。
于是我们就可以维护 \(D_i=A_iB_iC_i\) 这个数组了,对于 \([1,r-p)\) 这一段的 \(D_i\) 没有发生改变,但是 \(s_i\) 改变了,直接历史和复杂度又太巨大了,可以考虑将 \(s_i\) 的定义式改为 \(s_i=val_i+D_{[1,i]}*r\),这样只要前缀 \(D\) 不改变,\(s\) 也不用修改。
总复杂度 \(O(n\log V + m)\)。
//P8421
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10, M = 5e6 + 10;
int n, m;
unsigned a[N], b[N], c[N];
basic_string<pair<int, int> > qr[N];
unsigned int ans[M];
unsigned int cs[N], xs[N];
unsigned int qry(int x){
return cs[x] + xs[x] * x;
}
int gcd(int x, int y){
return y ? gcd(y, x % y) : x;
}
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++ i){
scanf("%u", &a[i]);
}
for(int i = 1; i <= n; ++ i){
scanf("%u", &b[i]);
}
for(int i = 1; i <= n; ++ i){
scanf("%u", &c[i]);
}
for(int i = 1; i <= m; ++ i){
int l, r;
scanf("%d%d", &l, &r);
qr[r].push_back(make_pair(l, i));
}
for(int i = 1; i <= n; ++ i){
int la = i - 1;
while(la){
int A = a[la] & a[i];
int B = b[la] | b[i];
int C = gcd(c[la], c[i]);
if(A == a[la] && B == b[la] && C == c[la]){
break;
} else {
a[la] = A;
b[la] = B;
c[la] = C;
-- la;
}
}
for(int j = la + 1; j <= i; ++ j){
unsigned int val = xs[j] * (i-1) + cs[j];
xs[j] = a[j] * b[j] * c[j] + xs[j-1];
val += xs[j];
if(j == i){
val = xs[j-1] * i + cs[j-1] + a[j] * b[j] * c[j];
}
cs[j] = val - xs[j] * i;
}
for(auto [l, id] : qr[i]){
ans[id] += cs[i] + xs[i] * i;
ans[id] -= cs[l-1] + xs[l-1] * i;
}
}
for(int i = 1; i <= m; ++ i){
printf("%u\n", ans[i]);
}
return 0;
}
10. P13011 【MX-X13-T6】「KDOI-12」能做到的也只不过是静等缘分耗尽的那一天。
https://www.luogu.com.cn/problem/P13011。
题意:给定 \(n,x,y\),求所有 \(n\) 排列构成的笛卡尔树中,下标为 \(x\) 的点到下标为 \(y\) 的点是一条左链(即链上全是父节点-左儿子的边)的排列个数。多组询问。
\(T\leq 10^6,n\leq 5\times 10^6\)。
组合意义做法!代数推导含量极少!
首先特判 \(x=y\) 的情况,下文默认 \(x<y\)(\(x>y\) 交换一下即可)。
考虑 \([1,x),(x,y),(y,n]\) 三段区间形如什么样子会满足题意:
- 首先,\((y,n]\) 区间数怎么样都是没有影响的。
- 其次,\((x,y)\) 区间内的数必须 \(<p_y\),否则这个数会使得 \(x,y\) 在不同子树中。
- 最后,\([1,x)\) 的情况比较复杂,考虑那些取值在 \((p_x,p_y)\) 之间的数,这些数不能作为 \(y\) 的子树,否则 \(y\to x\) 的链会被断开,所以这些数和 \(x\) 之间一定存在一个 \(>p_y\) 的数。所以这个情况可以总结为:要么所有数 \(<p_x\),要么最右侧的 \(>p_y\) 的数更右侧的数都 \(<p_x\)。
显然,最后一段区间中所有数均 \(<p_x\) 的情况更为简单。此时这个区间内的数大小要求有:
- \(p_y\) 是 \([1,y]\) 中最大的;
- \(p_x\) 是 \([1,x]\) 中最大的。
很显然啊!这部分的方案数就形如一个树拓扑序计数,是 \(\dfrac{n!}{xy}\)!
最后考虑另一种情况,枚举那个最右侧的 \(>p_y\) 的数的下标 \(i\),则要求有:
- \(p_i\) 是 \([i,y]\) 中最大的;
- \(p_y\) 是 \((i,y]\) 中最大的;
- \(p_x\) 是 \((i,x]\) 中最大的。
方案数同上,是 \(\sum_{i=1}^{x-1}\dfrac{n!}{(y-i+1)(y-i)(x-i)}\)。
这个式子可以裂项!具体地,首先裂 \(y-i+1,y-i\) 两项,再把 \(x-i\) 裂出去:
维护倒数的前缀和就可以 \(O(1)\) 回答询问。
//P13011
#include <bits/stdc++.h>
using namespace std;
const int N = 5e6 + 10;
int T, n, x, y;
typedef long long ll;
ll P, fac[N], inv[N], iv[N], ivs[N];
ll qp(ll x, ll y){
ll ans = 1;
while(y){
if(y & 1){
ans = ans * x % P;
}
x = x * x % P;
y >>= 1;
}
return ans;
}
ll C(int x, int y){
if(x < 0 || y < 0 || x < y){
return 0;
}
return fac[x] * inv[y] % P * inv[x-y] % P;
}
ll ivsum(int x, int y){
return (ivs[y] + P - ivs[x-1]) % P;
}
int main(){
scanf("%d%lld", &T, &P);
fac[0] = 1;
for(int i = 1; i < 5000005; ++ i){
fac[i] = fac[i-1] * i % P;
}
inv[5000004] = qp(fac[5000004], P-2);
for(int i = 5000003; i >= 0; -- i){
inv[i] = inv[i+1] * (i+1) % P;
iv[i] = inv[i] * fac[i-1] % P;
}
for(int i = 1; i < 5000005; ++ i){
ivs[i] = (ivs[i-1] + iv[i]) % P;
}
while(T--){
scanf("%d%d%d", &n, &x, &y);
if(x > y){
swap(x, y);
} else if(x == y){
printf("%lld\n", fac[n]);
continue;
}
ll ans = iv[x] % P * iv[y] % P;
ans = (ans + iv[y-x] * (ivsum(1, x-1) + P - ivsum(y-x+1, y-1))) % P;
ans = (ans - iv[y-x+1] * (ivsum(1, x-1) + P - ivsum(y-x+2, y))) % P;
printf("%lld\n", (ans + P) * fac[n] % P);
}
return 0;
}
11. CF1181E2 A Story of One Country (Hard)
https://www.luogu.com.cn/problem/CF1181E2。
题意:平面上有 \(n\) 个整点坐标矩形,每次可以划一条平行于坐标轴的线段,要求线段的两端为无穷远处或者另外一条线段上,且线段不可以穿过矩形。问能否画若干条线段使得每个矩形都在不同的区域。
\(n\leq 10^5\)
容易发现这么画线段是可以贪心的:画了肯定比不画更优。那么问题变为如何维护以及快速找到应该画的位置。
对于每一块没有被直线分隔过的矩形集合,维护所有矩形的横边和竖边集合,然后从四个方向分别扫,扫到了一个可以分隔的地方,就把矩形少的那部分提取出来新建一个集合。由启发式分裂的复杂度分析可以分析到这么做是 \(O(n\log^2 n)\) 的。
//CF1181E2
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n;
struct rect{
int up, dn, le, ri;
} r[N];
set<pair<int, int> > X[N], Y[N];
int cnt = 1;
void inse(int id, int v){
X[id].insert(make_pair(r[v].up, v));
X[id].insert(make_pair(r[v].dn, -v));
Y[id].insert(make_pair(r[v].le, v));
Y[id].insert(make_pair(r[v].ri, -v));
}
bool solve(int id){
int siz = X[id].size() / 2;
// printf("%d %d\n", id, siz);
if(siz <= 1){
return 1;
}
auto il = X[id].begin();
auto ir = X[id].rbegin();
auto jl = Y[id].begin();
auto jr = Y[id].rbegin();
int a = 0, b = 0, c = 0, d = 0;
while(siz --){
a += (*il).second > 0 ? 1 : -1;
b += (*ir).second < 0 ? 1 : -1;
c += (*jl).second > 0 ? 1 : -1;
d += (*jr).second < 0 ? 1 : -1;
// printf("%d %d %d %d %d\n", siz, a, b, c, d);
++ il;
++ ir;
++ jl;
++ jr;
if(a == 0){
++ cnt;
auto tmp = X[id].begin();
while(tmp != il){
int v = (*tmp).second;
// printf("%d %d\n", (*tmp).first, (*tmp).second);
if(v > 0){
inse(cnt, v);
}
++ tmp;
}
for(auto i : X[cnt]){
X[id].erase(i);
}
for(auto i : Y[cnt]){
Y[id].erase(i);
}
return solve(id) && solve(cnt);
}
if(b == 0){
++ cnt;
auto tmp = X[id].rbegin();
while(tmp != ir){
int v = (*tmp).second;
// printf("%d %d\n", (*tmp).first, (*tmp).second);
if(v > 0){
inse(cnt, v);
}
++ tmp;
}
for(auto i : X[cnt]){
X[id].erase(i);
}
for(auto i : Y[cnt]){
Y[id].erase(i);
}
return solve(id) && solve(cnt);
}
if(c == 0){
++ cnt;
auto tmp = Y[id].begin();
while(tmp != jl){
int v = (*tmp).second;
// printf("%d %d\n", (*tmp).first, (*tmp).second);
if(v > 0){
inse(cnt, v);
}
++ tmp;
}
for(auto i : X[cnt]){
X[id].erase(i);
}
for(auto i : Y[cnt]){
Y[id].erase(i);
}
return solve(id) && solve(cnt);
}
if(d == 0){
++ cnt;
auto tmp = Y[id].rbegin();
while(tmp != jr){
int v = (*tmp).second;
// printf("%d %d\n", (*tmp).first, (*tmp).second);
if(v > 0){
inse(cnt, v);
}
++ tmp;
}
for(auto i : X[cnt]){
X[id].erase(i);
}
for(auto i : Y[cnt]){
Y[id].erase(i);
}
return solve(id) && solve(cnt);
}
}
return 0;
}
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; ++ i){
int a, b, c, d;
scanf("%d%d%d%d", &a, &b, &c, &d);
r[i] = {a, c, b, d};
X[1].insert(make_pair(a, i));
X[1].insert(make_pair(c, -i));
Y[1].insert(make_pair(b, i));
Y[1].insert(make_pair(d, -i));
}
puts(solve(1) ? "YES" : "NO");
return 0;
}
12. CF1446D2 Frequency Problem (Hard Version)
https://www.luogu.com.cn/problem/CF1446D2。
题意:找到序列中最长的一个众数不唯一的子串,输出长度。
\(n\leq 2\times 10^5\)。
性质 1:一定存在一个最优子串使得其中一个众数为全局众数。否则这个子串扩张的过程中一定能够找到一个更长的合法子串。
这个性质又带来一个结论:枚举作为众数另一个数,若一个子串记入答案只需满足这个枚举的数和全局众数个数相同即可。如果存在一个出现次数更多的数,那么这个子串肯定不是最优解。
枚举作为众数的另一个数,设有 \(c\) 个,根号分治,若 \(c\geq B\),将两个众数分别设为 \(+1,-1\),可以一遍扫描完成。否则,对于每个这个数,找到它两侧 \(c+1\) 个出现的全局众数,将这个序列提取出来,跑一样的东西(注意中间可能有断点、两边边界问题等)。
复杂度 \(O(n\sqrt n)\)。
//CF1446D2
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, a[N], cnt[N], mx, mxc;
int ans = 0;
int fi[N+N], le[N], hav[N], nx[N], cc[N];
vector<int> occ[N];
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; ++ i){
scanf("%d", &a[i]);
++ cnt[a[i]];
cc[i] = cnt[a[i]];
mx = max(mx, cnt[a[i]]);
occ[a[i]].push_back(i);
}
for(int i = 1; i <= n; ++ i){
if(cnt[i] == mx){
if(mxc){
printf("%d\n", n);
return 0;
}
mxc = i;
}
}
for(int i = 1; i <= n; ++ i){
le[i] = le[i-1];
if(a[i-1] == mxc){
le[i] = i-1;
}
}
for(int i = n; i >= 1; -- i){
nx[i] = nx[i+1];
if(a[i+1] == mxc){
nx[i] = i+1;
}
}
memset(fi, -1, sizeof(fi));
for(int i = 1; i <= n; ++ i){
if(i == mxc){
continue;
} else if(cnt[i] >= 200){
int nw = 0;
for(int j = 1; j <= n; ++ j){
if(a[j] == mxc){
++ nw;
} else if(a[j] == i){
-- nw;
}
if(nw == 0){
ans = max(ans, j);
} else if(fi[N+nw] != -1){
ans = max(ans, j - fi[N+nw]);
} else {
fi[N+nw] = j;
}
}
nw = 0;
for(int j = 1; j <= n; ++ j){
if(a[j] == mxc){
++ nw;
} else if(a[j] == i){
-- nw;
}
fi[N+nw] = -1;
}
} else {
// memset(fi, -1, sizeof(fi));
vector<int> tmp;
int bg = 0;
for(int j : occ[i]){
int st = 0;
if(le[j] == 0){
st = occ[mxc][0];
} else {
st = le[j];
for(int k = 1; k <= cnt[i]; ++ k){
if(le[st] == 0){
break;
}
st = le[st];
}
}
for(int k = 1; k <= cnt[i] * 2 + 2; ++ k){
// printf("[%d %d]", k, st);
if(st == 0){
break;
}
if(!hav[st]){
while(bg != occ[i].size() && occ[i][bg] < st){
tmp.push_back(occ[i][bg]);
++ bg;
}
tmp.push_back(st);
hav[st] = 1;
}
st = nx[st];
}
}
while(bg != occ[i].size()){
tmp.push_back(occ[i][bg]);
++ bg;
}
int nw = 0;
if(hav[occ[mxc][0]]){
fi[N] = 0;
}
int la = 0;
for(int j : tmp){
if(fi[N+nw] != -1 && (a[j]!=mxc || cc[j] - la == 1)){
// printf("%d %d %d %d \n", nw, j, fi[N+nw], j-1-fi[N+nw]);
ans = max(ans, j - 1 - fi[N+nw]);
}
if(a[j] == mxc){
if(la){
// printf("[%d]", cc[a[j]] - la);
nw += cc[j] - la;
} else {
++ nw;
}
la = cc[j];
} else {
-- nw;
}
// printf("[%d %d]\n", j, nw);
if(fi[N+nw] == -1){
fi[N+nw] = j;
}
// else {
// ans = max(ans, j - fi[N+nw]);
// }
}
if(hav[occ[mxc][occ[mxc].size()-1]]){
ans = max(ans, n - fi[N+nw]);
}
nw = 0;
la = 0;
fi[N] = -1;
for(int j : tmp){
if(a[j] == mxc){
if(la){
nw += cc[j] - la;
} else {
++ nw;
}
la = cc[j];
} else {
-- nw;
}
fi[N+nw] = -1;
}
// printf("col%d ", i);
for(int j : tmp){
hav[j] = 0;
// printf("%d ", j);
}
// puts("");
// printf("%d\n", ans);
}
}
printf("%d\n", ans);
return 0;
}
13. \(\color{red}\texttt{hard}\) CF1019C Sergey's problem
https://www.luogu.com.cn/problem/CF1019C
题意:给你一张有向图,让你选择一个点集使得点集内任意两点无直接边,且图上任意一点 \(u\) 满足存在一个点集内的点 \(v\),\(v\) 走 \(\leq 2\) 步能走到 \(u\)。
\(n,m\leq 10^6\)
诡谲题目。
首先如果图是个 DAG,按照拓扑序执行如下算法:
- 若目前点 \(vis=0\),将目前点 \(vis,ok\) 均设为 \(1\),否则跳过该点。
- 将目前点能到的所有点 \(vis\) 设为 \(1\)。
就可以得到答案,且每个点都能由点集内点一步到达。
原图不是 DAG 怎么办?考虑以任意顺序执行上述算法,那么 \(ok=1\) 的点构成一个 DAG,然后再对这个 DAG 跑一遍上述算法就好了!
//CF1019C
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int n, m;
vector<int> g[N];
int a[N], b[N], c[N], d[N];
int cnt = 0;
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; ++ i){
int x, y;
scanf("%d%d", &x, &y);
g[x].push_back(y);
}
for(int i = 1; i <= n; ++ i){
if(!a[i]){
a[i] = b[i] = 1;
for(auto j : g[i]){
a[j] = 1;
}
}
}
for(int i = n; i >= 1; -- i){
if(b[i] && !c[i]){
c[i] = d[i] = 1;
++ cnt;
for(auto j : g[i]){
if(b[j]){
c[j] = 1;
}
}
}
}
printf("%d\n", cnt);
for(int i = 1; i <= n; ++ i){
if(d[i]){
printf("%d ", i);
}
}
return 0;
}
14. P13780 「o.OI R2」愿天堂没有分块
https://www.luogu.com.cn/problem/P13780
题意:给一个序列 \(a\),每次询问 \([l,r]\) 求 \(\operatorname{MEX}_{[l',r']\in[l,r]}\{\operatorname{MEX}_{i\in[l',r']}a_i\}\)。
\(a_i\leq n\leq 10^6\)。
trick:区间极长 \(\operatorname{MEX}\) 区间只有 \(O(n)\) 组。证明可以考虑颜色段均摊:
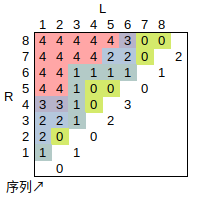
如图,每个区域的右下角都对应着一个区间极长 \(\operatorname{MEX}\) 区间。
求法:
- 我们对于每个 \(k\),维护 \(\operatorname{MEX}=k\) 的极长区间集合。
- 首先把所有长度为 \(1\) 的区间提取出来,然后对应放入集合 \(0,1\) 中。
- 枚举 \(k\in 1\to n+1\),首先删去若干集合 \(k\) 中的区间,使得内部没有包含关系。
- 再考虑每个集合 \(k\) 中的区间,找到最靠近这个区间两端点的两个 \(k\),形成两个新的区间。
- 计算这两个新区间的 \(\operatorname{MEX}\),并插入到对应集合中。
计算区间 \(\operatorname{MEX}\) 的方法是主席树,扫到右端点 \(r\) 时主席树位置 \(i\) 表示 \(r\) 左边第一个 \(i\) 的出现位置,然后线段树二分。
现在我们有了若干个区间,问题转化为了询问包含于某个区间的所有区间的权值的 \(\operatorname{MEX}\),扫描线后同上区间 \(\operatorname{MEX}\) 的方法即可。注意答案可能取到 \(n+2\)。
//P13780
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int n, q, a[N];
vector<pair<int, int> > qr[N];
vector<int> occ[N];
int mx[N];
struct node{
int ls, rs, mn;
} t[N*24];
int tot, rt[N], rr;
void mdf(int &p, int l, int r, int x, int v){
t[++tot] = t[p];
p = tot;
if(l == r){
t[p].mn = max(t[p].mn, v);
} else {
int mid = l + r >> 1;
if(x <= mid){
mdf(t[p].ls, l, mid, x, v);
} else {
mdf(t[p].rs, mid+1, r, x, v);
}
t[p].mn = min(t[t[p].ls].mn, t[t[p].rs].mn);
}
}
int ef(int p, int l, int r, int val){
if(t[p].mn >= val){
return n + 1;
} else if(l == r){
return l;
} else {
int mid = l + r >> 1;
if(t[t[p].ls].mn < val){
return ef(t[p].ls, l, mid, val);
} else {
return ef(t[p].rs, mid+1, r, val);
}
}
}
int qmex(int l, int r){
return ef(rt[r], 1, n, l);
}
struct trr{
int mn[N*4];
void mdf(int p, int l, int r, int x, int v){
if(l == r){
mn[p] = max(mn[p], v);
} else {
int mid = l + r >> 1;
if(x <= mid){
mdf(p<<1, l, mid, x, v);
} else {
mdf(p<<1|1, mid+1, r, x, v);
}
mn[p] = min(mn[p<<1], mn[p<<1|1]);
}
}
int ef(int p, int l, int r, int val){
if(mn[p] >= val){
return n + 1;
} else if(l == r){
return l;
} else {
int mid = l + r >> 1;
if(mn[p<<1] < val){
return ef(p<<1, l, mid, val);
} else {
return ef(p<<1|1, mid+1, r, val);
}
}
}
} tr;
bool cmp(pair<int, int> x, pair<int, int> y){
if(x.second != y.second){
return x.second < y.second;
} else {
return x.first > y.first;
}
}
vector<pair<int, int> > jc[N], nw[N];
int main(){
scanf("%d%d", &n, &q);
for(int i = 1; i <= n; ++ i){
scanf("%d", &a[i]);
occ[a[i]].push_back(i);
rt[i] = rt[i-1];
mdf(rt[i], 1, n, a[i], i);
if(a[i] == 1){
nw[2].push_back(make_pair(i, i));
jc[i].push_back(make_pair(i, 2));
} else {
nw[1].push_back(make_pair(i, i));
jc[i].push_back(make_pair(i, 1));
}
}
for(int i = 2; i <= n + 1; ++ i){
for(auto j : nw[i]){
int l = j.first, r = j.second;
int k = lower_bound(occ[i].begin(), occ[i].end(), l) - occ[i].begin() - 1;
if(k >= 0){
nw[qmex(occ[i][k], r)].push_back(make_pair(occ[i][k], r));
}
k = lower_bound(occ[i].begin(), occ[i].end(), r) - occ[i].begin();
if(k < occ[i].size()){
nw[qmex(l, occ[i][k])].push_back(make_pair(l, occ[i][k]));
}
}
sort(nw[i+1].begin(), nw[i+1].end(), cmp);
int la = 0;
vector<pair<int, int> > tmp;
for(auto j : nw[i+1]){
if(j.first > la){
la = j.first;
jc[j.second].push_back(make_pair(j.first, i+1));
tmp.push_back(j);
}
}
nw[i+1].swap(tmp);
}
for(int i = 1; i <= q; ++ i){
int l, r;
scanf("%d%d", &l, &r);
qr[r].push_back(make_pair(l, i));
}
static int ans[N];
for(int i = 1; i <= n; ++ i){
for(auto j : jc[i]){
tr.mdf(1, 1, n+2, j.second, j.first);
}
for(auto j : qr[i]){
ans[j.second] = tr.ef(1, 1, n+2, j.first);
}
}
for(int i = 1; i <= q; ++ i){
printf("%d\n", ans[i]);
}
return 0;
}
\(\color{red}\texttt{hard}\) 15. P9194 [USACO23OPEN] Triples of Cows P
https://www.luogu.com.cn/problem/P9194。
题意:给你一棵树,\(i\) 轮,每次先求出满足存在边 \((a,b),(b,c)\) 的有序三元组 \((a,b,c)\) 组数,然后删除点 \(i\),并连边所有 \(i\) 的相邻点。
\(n\leq 5\times 10^5\)。
到底是谁在会做这种题?
发现过程中连的边会越来越多,有一个 trick:将边 \((u,v)\) 拆分成两条边 \((u,\underline w),(\underline w,v)\) 其中 \(\underline w\) 是新点。然后删除点 \(p\),就相当于断掉 \(p\) 与周围所有点(均为新点)的边后,将它周围的那些新点合并为一个点。合并完的新点度数会逐渐 \(>2\),且图与按照原题意模拟得到的图等价。ps:容易发现,这个图是黑白点交替出现的。
将 \(n\) 号点设为根(因为不会被删)。考虑计数,对于新点 \(\underline x\) 设 \(s_{1,\underline x}\) 为这个点的儿子个数。\((a,b,c)\) 有三种情况:
- 三个点均是同一新点 \(\underline x\) 的邻点: \(\sum_{\underline x} (s_{1,\underline x}+1)s_{1,\underline x}(s_{1,\underline x}-1)\)。
- 一个点是另外两个点的父亲的父亲,枚举这个点 \(a\):\(\sum_a\left(\sum_{\underline x\in son_a}s_{\underline x}^2\right)-\sum_{\underline x\in son_a}s_{\underline x}\)。
- 三个点构成祖先后代链,枚举最浅的两个点中间的那个新点 \(\underline x\):\(2\sum_{\underline x}s_{\underline x}\sum_{a\in son_{\underline x}}\sum_{\underline y\in son_a} s_{\underline y}\)。
看上去很复杂,实际上,对于新点维护 \(s_{1,\underline x},s_{3,\underline x}\) 表示它的 \(1\) 级,\(3\) 级儿子,对于原点维护 \(s_{2,a}\) 表示它的 \(2\) 级儿子,那么这三个式子的和可以写作:
那么接下来的问题是如何修改 \(s\) 数组。使用并查集维护每个新点合并到了哪个点,并维护每个集合中唯一一个没有往上合并的点的 \(s\)。删除点 \(a\) 的时候,需要修改的只有它的儿子,它的父亲、父亲的父亲、父亲的父亲的父亲,可以直接修改。
//P9194
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int n;
vector<int> tg[N], g[N];
typedef long long ll;
ll s[4][N], ans;
int anc[N], fa[N];
ll F(ll v){
return v * v * v - v * v - v;
}
void upd(int x, int op){
if(x <= n){
ans += op * s[2][x] * s[2][x];
} else {
ans += op * F(s[1][x]) + op * 2 * s[1][x] * s[3][x];
}
}
void dfs(int x, int fa){
for(int i : tg[x]){
if(i == fa){
continue;
}
g[x].push_back(i+n);
anc[i+n] = x;
g[i+n].push_back(i);
anc[i] = i + n;
dfs(i, x);
s[1][i+n] = 1;
++ s[2][x];
s[3][i+n] += s[2][i];
}
}
int gf(int x){
return x == fa[x] ? x : fa[x] = gf(fa[x]);
}
int main(){
scanf("%d", &n);
for(int i = 1; i < n; ++ i){
int u, v;
scanf("%d%d", &u, &v);
tg[u].push_back(v);
tg[v].push_back(u);
}
dfs(n, 0);
for(int i = 1; i < n + n; ++ i){
upd(i, 1);
fa[i] = i;
}
printf("%lld\n", ans);
for(int i = 1; i < n; ++ i){
upd(i, -1);
int fw = gf(anc[i]);
upd(fw, -1);
s[1][fw] --;
s[3][fw] -= s[2][i];
s[2][i] = 0;
upd(anc[fw], -1);
s[2][anc[fw]] --;
if(anc[fw] != n){
int fffw = gf(anc[anc[fw]]);
upd(fffw, -1);
s[3][fffw] --;
}
for(auto x : g[i]){
upd(x, -1);
fa[x] = fw;
s[1][fw] += s[1][x];
s[3][fw] += s[3][x];
s[2][anc[fw]] += s[1][x];
if(anc[fw] != n){
s[3][gf(anc[anc[fw]])] += s[1][x];
}
s[1][x] = s[3][x] = 0;
}
upd(fw, 1);
upd(anc[fw], 1);
if(anc[fw] != n){
upd(gf(anc[anc[fw]]), 1);
}
printf("%lld\n", ans);
}
return 0;
}
16. qoj12998. Finite Walking
https://qoj.ac/contest/2289/problem/12998。
题意:给定一张 \(n\) 个点 \(m\) 条边的无向图(可能存在重边自环),第 \(i\) 条边有一个权值 \(a_i\) 和一个初始为 \(0\) 的计数器 \(b_i\)。你可以任选一个起点,沿着图上的边走任意多步,每次经过第 \(i\) 条边时,会将 \(b_i\) 改为 \((b_i+1)\pmod a_i\)。求这个过程可以生成多少种不同的 \((b_1,b_2,...,b_m)\)。
\(n\leq 2\times 10^5,m\leq 4\times 10^5\)。
考虑连通图的情况。
性质 1:对于 \(a_i\) 为奇数的边,可以通过来回走动,使得这条边的 \(b_i\) 变为任意取值。这样的话,就可以删除所有 \(a_i\) 为奇数的边,将两边端点合并为一个,答案 \(*a_i\)。
性质 2:对于 \(a_i\) 为偶数的边,可以通过来回走动改变 \(b_i/2\) 的值。这样的话,就可以将这些边的权值全部变为 \(2\),答案 \(*(a_i/2)\)。
现在变为一张边权均为 \(2\) 的图,提出一棵生成树,显然对于非树边和任意起终点,树边都有唯一合法方案。方案数 \((\dbinom n2 + 1)2^{m-n+1}\)。
不连通图,对于每个连通块答案为 \(c_1,...,c_k\),则总答案为 \(1+(c_1-1)+(c_2-1)+...\)(去掉 \(b\) 全 \(0\) 的那一组,然后统一加上)。不连通要分开处理的原因是,不连通就不能保证能够走到 \(i\) 边从而使得 \(b_i\) 能取到任意值/同奇偶性任意值,这样性质就不满足了。
//qoj12998
#include <bits/stdc++.h>
using namespace std;
const int N = 4e5 + 10;
int n, m;
typedef long long ll;
const ll P = 1e9 + 7;
ll ans[N], sum = 1;
int fa[2][N], cnt[N], siz[N];
ll pw[N];
int gf(int x, int op){
return x == fa[op][x] ? x : fa[op][x] = gf(fa[op][x], op);
}
void mg(int x, int y, int op){
fa[op][gf(x, op)] = gf(y, op);
}
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++ i){
fa[0][i] = fa[1][i] = i;
ans[i] = 1;
}
pw[0] = 1;
for(int i = 1; i <= m; ++ i){
pw[i] = pw[i-1] * 2 % P;
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
if(w & 1){
ans[u] = ans[u] * w % P;
mg(u, v, 0);
mg(u, v, 1);
} else {
ans[u] = ans[u] * (w / 2) % P;
mg(u, v, 1);
++ cnt[u];
}
}
for(int i = 1; i <= n; ++ i){
if(i != gf(i, 1)){
cnt[gf(i, 1)] += cnt[i];
ans[gf(i, 1)] = ans[gf(i, 1)] * ans[i] % P;
}
if(i == gf(i, 0)){
++ siz[gf(i, 1)];
}
}
for(int i = 1; i <= n; ++ i){
if(i == gf(i, 1)){
sum = (sum + (1ll*siz[i]*(siz[i]-1)/2%P + 1) * pw[cnt[i]-siz[i]+1] % P * ans[i] - 1) % P;
}
}
printf("%lld\n", sum);
return 0;
}
17. P13496 【MX-X14-T6】大音乐家
https://www.luogu.com.cn/problem/P13496。
题意:给定序列 \(a\) 和 \(X,Y\),\(m\) 次操作,每次从 \(n(n-1)/2\) 个无序二元组中随机一个 \((i,j)\),并交换 \(a_i,a_j\)。求对于所有 \((n(n-1)/2)^m\) 种操作序列的可能性,满足 \(|i-j|\leq X,|a_i-a_j|\geq Y\) 的二元组 \((i,j)(i<j)\) 组数之和。
\(n\leq 2\times 10^5,m\leq 5\times 10^5\)。
考虑计算 \(a_x,a_y(|a_x-a_y|\geq Y)\) 两个值在多少种操作序列中会对答案有贡献。在操作的过程中,\(x,y\) 这两个下标上的值有如下 \(7\) 种情况:
且两两之间转移的方案数是容易计算的。使用矩阵快速幂可以算出最初的 \(\texttt{xy}\) 到 \(m\) 次操作后为哪一种情况的方案数。
最后要统计答案。设 \(F[0\sim 6]\) 为一对 \(a\) 在 \(m\) 次操作后变为这 \(7\) 种情况的方案数,枚举下标 \(i,j(|a_i-a_j|\geq Y)\),那么 \(F\) 前面的系数和 \(i,j\) 以及二者之差是否 \(>X\) 有关。问题变为对于 \(i\) 统计有多少满足条件的 \(j\),以及这些满足条件的 \(j\) 中有多少 \(>i+X\)。正反两次扫描线即可。
具体的转移矩阵、贡献系数可以看代码。
// Problem: P13496 【MX-X14-T6】大音乐家
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P13496
// Memory Limit: 512 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10, M = 5e5 + 10;
int n, m, X, Y, a[N];
typedef long long ll;
const ll P = 998244353;
ll qp(ll x, ll y){
ll ans = 1;
while(y){
if(y & 1){
ans = ans * x % P;
}
x = x * x % P;
y >>= 1;
}
return ans;
}
ll ans;
ll F[7];
/*
0 xy
1 yx
2 x?
3 ?x
4 y?
5 ?y
6 ??
*/
struct mat{
ll a[7][7];
mat operator * (const mat &b) const {
mat c;
memset(c.a, 0, sizeof(c.a));
for(int i = 0; i < 7; ++ i){
for(int j = 0; j < 7; ++ j){
for(int k = 0; k < 7; ++ k){
c.a[j][k] = (c.a[j][k] + a[j][i] * b.a[i][k]) % P;
}
}
}
return c;
}
} tr;
mat qp(mat x, int y){
mat ans;
for(int i = 0; i < 7; ++ i){
for(int j = 0; j < 7; ++ j){
ans.a[i][j] = (i == j);
}
}
while(y){
if(y & 1){
ans = ans * x;
}
x = x * x;
y >>= 1;
}
return ans;
}
ll t[M*4];
void add(int p, int l, int r, int x, int v){
if(l == r){
t[p] += v;
} else {
int mid = l + r >> 1;
if(x <= mid){
add(p<<1, l, mid, x, v);
} else {
add(p<<1|1, mid+1, r, x, v);
}
t[p] = t[p<<1] + t[p<<1|1];
}
}
int ask(int p, int l, int r, int ql, int qr){
if(qr < l || r < ql){
return 0;
} else if(ql <= l && r <= qr){
return t[p];
} else {
int mid = l + r >> 1;
return ask(p<<1, l, mid, ql, qr) + ask(p<<1|1, mid+1, r, ql, qr);
}
}
int main(){
scanf("%d%d%d%d", &n, &m, &X, &Y);
for(int i = 1; i <= n; ++ i){
scanf("%d", &a[i]);
}
ll tval = 1ll * (n - 2) * (n - 3) / 2 % P;
tr.a[0][0] = tr.a[1][1] = tval;
tr.a[2][0] = tr.a[2][3] = tr.a[2][4] = 1;
tr.a[3][1] = tr.a[3][2] = tr.a[3][5] = 1;
tr.a[4][1] = tr.a[4][2] = tr.a[4][5] = 1;
tr.a[5][0] = tr.a[5][3] = tr.a[5][4] = 1;
tr.a[6][6] = (1ll * n * (n - 1) / 2 - 4) % P;
tr.a[2][6] = tr.a[3][6] = tr.a[4][6] = tr.a[5][6] = n - 3;
tr.a[0][2] = tr.a[0][5] = tr.a[1][3] = tr.a[1][4] = n - 2;
tr.a[2][2] = tr.a[3][3] = tr.a[4][4] = tr.a[5][5] = tval + n - 3;
tr.a[0][1] = tr.a[1][0] = tr.a[6][2] = tr.a[6][3] = tr.a[6][4] = tr.a[6][5] = 1;
tr = qp(tr, m);
for(int i = 0; i < 7; ++ i){
F[i] = tr.a[0][i];
}
ll ac = 0;
for(int i = 1; i <= X; ++ i){
ac += n - i;
}
ac %= P;
ll iv = qp(n - 2, P - 2);
ll ivv = qp(tval, P - 2);
for(int i = 1; i <= n; ++ i){
int cnt = ask(1, 1, 500000, 1, a[i] - Y) + ask(1, 1, 500000, a[i] + Y, 500000);
int len = min(X, n - i) + min(X, i - 1);
ans = (ans + (F[3] + F[5]) * cnt % P * len % P * iv) % P;
ans = (ans + (P - F[6]) * cnt % P * len % P * ivv) % P;
ans = (ans + (F[6] * (ac + 1) % P * ivv % P) % P * cnt) % P;
ans = (ans + (F[0] + F[1] - (F[2] + F[3] + F[4] + F[5]) % P * iv % P + P) * cnt) % P;
add(1, 1, 500000, a[i], 1);
if(i + X < n){
cnt = ask(1, 1, 500000, 1, a[i+X+1] - Y) + ask(1, 1, 500000, a[i+X+1] + Y, 500000);
ll tmp = - F[0] - F[1] + (F[2] + F[3] + F[4] + F[5]) * iv - F[6] * ivv;
ans = (ans + (tmp % P + P) % P * cnt) % P;
}
}
memset(t, 0, sizeof(t));
for(int i = n; i >= 1; -- i){
int cnt = ask(1, 1, 500000, 1, a[i] - Y) + ask(1, 1, 500000, a[i] + Y, 500000);
int len = min(X, n - i) + min(X, i - 1);
ans = (ans + (F[2] + F[4]) * cnt % P * len % P * iv) % P;
ans = (ans + (P - F[6]) * cnt % P * len % P * ivv) % P;
add(1, 1, 500000, a[i], 1);
}
printf("%lld\n", (ans + P) % P);
return 0;
}
/*
15 355 9 8
1 2 13 5 6 7 8 9 3 4 10 11 12 14 15
*/
18. P13688 【MX-X16-T6】「DLESS-3」XOR and Powerless Suffix Mode
https://www.luogu.com.cn/problem/P13688。
题意:给定序列 \(b\),定义 \(x\) 为 \(b\) 的一个子序列的一个好数当且仅当 \(x\) 满足:1. \(x\) 是这个子序列的众数;2. 不存在下标 \(i,j\) 使得 \(a_i=a_j=x\),\(i\) 在子序列中,\(j\) 不在;3. \(x\) 在子序列中的出现次数不多于在原序列中的出现次数的 \(p\%\)。现在给定一个序列 \(a\),多次询问,每次指定 \(a_{[l,r]}\) 作为序列 \(b\) 并给定 \(p\%\),求 \(a_{[l,r]}\) 的所有子序列的所有好数的异或和。注意一个子序列可能有多个好数,也可能没有好数。
\(n,q\leq 2.5\times 10^5\)。
看着非常吓人的一道题,实际上不难。
分析一下好数的性质。性质 \(2\) 意味着 \(x\) 的出现次数能够唯一对应一种选择哪些 \(x\) 进入子序列的方案。而且题目中并没有任何一处要求了子序列内的数顺序。所以注重点是原序列内每个数的出现次数 \(cnt_x\),与序列具体形态无关。
然后考虑计算以 \(x\) 为好数的子序列个数的奇偶性。首先是 \(x\) 的出现次数 \(t\) 要在 \([1,cnt_x\times p\%]\) 之间,其次是其他数要出现 \(\leq t\) 次,且要乘以组合数。列式:
看着非常复杂,而且组合数前缀和这种恐怖的东西,但是我们知道组合数 \(\bmod 2\) 是有很好的性质的。具体的,本题需要运::
性质 1:\(\sum_{i=0}^b\dbinom ai\equiv \dbinom{a-1}b\bmod 2\)。证明考虑将左侧使用组合数递推式拆下去,发现只有 \(\dbinom{a-1}b\) 一项出现了一次。
性质 2:非常经典。\(\dbinom ab\equiv [a\&b=a]\bmod 2\)。
继续化简式子:
这个式子其实已经可以计算了!发现对于 \(cnt_x\) 相同的 \(x\),中括号内内容也是相同的,可以一起计算,而且不同的 \(cnt_x\) 只有 \(O(\sqrt n)\) 项。那么可以使用莫队维护 \(cnt_x\) 以及 \(cnt_x\) 相同的数个数、异或和,然后暴力 \(O(\sqrt n)\) 计算答案。
如何快速找到所有存在 \(cnt_x=y\) 的 \(y\)?考虑每次修改 \(cnt_x\) 就将新的 \(cnt_x\) 值插入到一个 vector 中,然后每次询问的时候遍历 vector 去重即可。
// Problem: P13688 【MX-X16-T6】「DLESS-3」XOR and Powerless Suffix Mode
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P13688
// Memory Limit: 512 MB
// Time Limit: 1500 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
const int N = 250010, B = 400;
int n, q, a[N], b[N];
struct node{
int l, r, p, id;
} qr[N];
int ans[N];
bool cmp(node x, node y){
if(x.l / B != y.l / B){
return x.l / B < y.l / B;
} else {
return ((x.l / B) & 1) ? x.r < y.r : x.r > y.r;
}
}
int cnt[N], ccnt[N], xval[N], tem[N];
vector<int> upd;
void add(int x, int op){
-- ccnt[cnt[a[x]]];
xval[cnt[a[x]]] ^= b[a[x]];
cnt[a[x]] += op;
++ ccnt[cnt[a[x]]];
xval[cnt[a[x]]] ^= b[a[x]];
upd.push_back(cnt[a[x]]);
}
int main(){
scanf("%d%d", &n, &q);
for(int i = 1; i <= n; ++ i){
scanf("%d", &a[i]);
b[i] = a[i];
}
sort(b + 1, b + n + 1);
int m = unique(b + 1, b + n + 1) - b - 1;
for(int i = 1; i <= n; ++ i){
a[i] = lower_bound(b + 1, b + m + 1, a[i]) - b;
}
for(int i = 1; i <= q; ++ i){
int l, r, p;
scanf("%d%d%d", &l, &r, &p);
qr[i] = {l, r, p, i};
}
sort(qr + 1, qr + q + 1, cmp);
for(int i = 1, l = 1, r = 0; i <= q; ++ i){
while(r < qr[i].r){
add(++ r, 1);
}
while(l > qr[i].l){
add(-- l, 1);
}
while(r > qr[i].r){
add(r --, -1);
}
while(l < qr[i].l){
add(l ++, -1);
}
vector<int> nw;
for(int j : upd){
if(j && ccnt[j] && tem[j] != i){
nw.push_back(j);
tem[j] = i;
}
}
upd.swap(nw);
static int le[N], ri[N];
le[0] = ri[upd.size()+1] = 2147483647;
for(int j = 0; j < upd.size(); ++ j){
le[j+1] = (upd[j] - 1) & le[j];
}
for(int j = upd.size()-1; j >= 0; -- j){
ri[j+1] = (upd[j] - 1) & ri[j+2];
}
for(int j = 0; j < upd.size(); ++ j){
int val = le[j] & ri[j+2];
if(ccnt[upd[j]] != 1){
val &= (upd[j] - 1);
}
int X = upd[j] * qr[i].p / 100;
if((X & (val - 1)) != X){
ans[qr[i].id] ^= xval[upd[j]];
}
}
}
for(int i = 1; i <= q; ++ i){
printf("%d\n", ans[i]);
}
return 0;
}
\(\color{red}\texttt{hard}\) 19. P13756 【MX-X17-T5】Matrix
https://www.luogu.com.cn/problem/P13756。
题意:给你 \(q\) 个 \(n*n\) 的矩阵,让你构造 \(\leq M\) 个置换矩阵(每行每列只有一个 \(1\)),使得这些置换矩阵可以线性相加(即每个矩阵乘以一个整数后加起来)得到尽可能多的给定矩阵。
\(q\leq 100, n\leq 200, M=n^2-2n+2\)。
观察到,一个矩阵可以写成若干个置换矩阵相加的必要条件是这个矩阵每行每列的和相等。考虑构造证明这个是充分的。
满足这个条件的 \(n*n\) 矩阵可以通过给定如下 \(n^2-2n+2\) 个数唯一确定:左上角 \((n-1)*(n-1)\) 的矩阵,以及右上角那一个位置。与构造上限相同。
那么就有了一个思路:将这些位置全部变为 \(0\),那么剩下的那些位置自然就变为了 \(0\)。
首先操作一次反对角线,让右上角那个位置变为 \(0\)。接下来的操作就可以利用到最后一列除掉右上角、最后一行的所有位置,只要别的位置都为 \(0\) 了那么这些位置自动就是 \(0\)。
考虑每一 \(i-j\pmod {n-1}\) 相同的作为一组(例如 \(i=j\) 的主对角线就是一组),然后使用 \(n-1\) 次操作全变为 \(0\),是可以做到的:
- \(i\) 从 \(2\) 到 \(n-1\),构造 \(n-2\) 个置换矩阵,每个包含这一组除掉第 \(i\) 行那个格子,新增 \(n\) 行/\(n\) 列的两个格子,这些矩阵的目标是消除这一集合内其他位置与第一行的那个位置的差。
- 最后一次操作,将所有位置与 \((n,n)\) 选中,可以将整组变为 \(0\)。
那么就解决了。
//P13756
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n, q, M;
ll a[110][210][210];
int main(){
scanf("%d%d%d", &n, &q, &M);
for(int i = 1; i <= q; ++ i){
for(int j = 1; j <= n; ++ j){
for(int k = 1; k <= n; ++ k){
scanf("%lld", &a[i][j][k]);
}
}
}
int m = (n - 1) * (n - 1) + 1;
printf("%d\n", (n - 1) * (n - 1) + 1);
static int p[210];
for(int i = 1; i < n; ++ i){
p[i] = i;
}
for(int i = 1; i < n; ++ i){
for(int j = 2; j < n; ++ j){
for(int k = 1; k < n; ++ k){
printf("%d ", k == j ? n : p[k]);
}
printf("%d\n", p[j]);
}
for(int j = 1; j < n; ++ j){
printf("%d ", p[j]);
}
printf("%d\n", n);
for(int j = 1; j <= n; ++ j){
++ p[j];
if(p[j] == n){
p[j] = 1;
}
}
}
for(int i = n; i >= 1; -- i){
printf("%d ", i);
}
puts("");
for(int i = 1; i <= q; ++ i){
ll sum = 0;
for(int j = 1; j <= n; ++ j){
sum += a[i][1][j];
}
bool flg = 1;
for(int j = 1; j <= n; ++ j){
ll tmp = 0, tmpp = 0;
for(int k = 1; k <= n; ++ k){
tmp += a[i][j][k];
tmpp += a[i][k][j];
}
if(tmp != sum || tmpp != sum){
flg = 0;
break;
}
}
if(flg){
ll tmp = a[i][1][n];
for(int j = 2; j <= n; ++ j){
a[i][j][n-j+1] -= tmp;
}
printf("1 ");
for(int j = 1; j < n; ++ j){
p[j] = j;
}
for(int j = 1; j < n; ++ j){
ll sum = 0;
for(int k = 2; k < n; ++ k){
ll val = a[i][k][p[k]] - a[i][1][p[1]];
printf("%lld ", -val);
sum += val;
}
printf("%lld ", a[i][1][p[1]] + sum);
for(int k = 1; k < n; ++ k){
++ p[k];
if(p[k] == n){
p[k] = 1;
}
}
}
printf("%lld\n", tmp);
} else {
puts("0");
}
}
return 0;
}
\(\color{red}\texttt{hard}\) 20. P13757 【MX-X17-T6】Selection
https://www.luogu.com.cn/problem/P13757。
对于所有 \(v^{nm}\) 个值域为 \([1,v]\) 的 \(n*m\) 矩阵,计数满足如下条件的矩阵个数:能够找到其中 \(k\) 行,这 \(k\) 行的每一行都非严格偏序剩下的 \(n-k\) 行的任意一行,且不相等。
\(n\leq 4000,m,v\leq 10^9\)。
太难了!
不妨前 \(k\) 行为选定的 \(k\) 行。如果没有不相等的限制,那么是简单的:对于每一列,前 \(k\) 行的最小值 \(\geq\) 后 \(n-k\) 行的最大值。枚举这个最小值 \(i\),每一列的方案数都是 \([(v-i+1)^k-(v-i)^k]i^{n-k}\),列与列之间独立,那么总方案数:
算多的部分就是前 \(k\) 行,后 \(n-k\) 行均有全部等于前 \(k\) 行最小值的行,枚举这样的行数,容斥:
观察到,如果能够 \(O(1)\) 求 \(F(i,j)=\sum_{p=1}^v(v-p+1)^{i}p^{j}\),就能快速计算答案。
考虑递推:\((v-p+1)^ip^j=(v+1)(v-p+1)^{i-1}p^j-(v-p+1)^{i-1}p^{j+1}\),所以有 \(F(i,j)=(v+1)F(i-1,j)-F(i-1,j+1)\)。
边界是 \(F(0,j)\),可以发现这是一个自然数幂和,拉格朗日插值即可。
//P13757
#include <bits/stdc++.h>
using namespace std;
const int N = 4010;
typedef long long ll;
const ll P = 1e9 + 7;
int T, n, m, k, v;
int F[N][N+N], pw[N][N], C[N][N];
ll ipr[N];
ll qp(ll x, ll y){
ll ans = 1;
while(y){
if(y & 1){
ans = ans * x % P;
}
x = x * x % P;
y >>= 1;
}
return ans;
}
ll pww(int x, int y){
if(y < 4010){
return pw[x][y];
} else {
return pw[x][4009] * pww(x, y-4009);
}
}
ll Y[N*3], pr[N*3], sf[N*3];
ll mihe(int bs, int mi){
for(int i = 1; i <= mi + 2; ++ i){
Y[i] = (Y[i-1] + pww(i, mi)) % P;
}
if(bs <= mi + 2){
return Y[bs];
}
ll ans = 0;
ll ml = 1;
for(int i = 1; i <= mi + 2; ++ i){
pr[i] = sf[i] = bs - i;
}
pr[0] = sf[mi+3] = 1;
for(int i = 1; i <= mi + 2; ++ i){
pr[i] = pr[i] * pr[i-1] % P;
}
for(int i = mi + 2; i >= 1; -- i){
sf[i] = sf[i] * sf[i+1] % P;
}
for(int i = 1; i <= mi + 2; ++ i){
ll mul = Y[i] * ipr[mi+2-i] % P * ipr[i-1] % P * (((mi-i)&1) ? P - 1 : 1) % P;
mul = mul * pr[i-1] % P * sf[i+1] % P;
ans = (ans + mul) % P;
}
return ans;
}
int main(){
ipr[0] = 1;
for(int i = 1; i < 4010; ++ i){
ipr[i] = qp(i, P - 2) * ipr[i-1] % P;
pw[i][0] = 1;
for(int j = 1; j < 4010; ++ j){
pw[i][j] = 1ll * pw[i][j-1] * i % P;
}
}
for(int i = 0; i < 4010; ++ i){
C[i][0] = 1;
for(int j = 1; j <= i; ++ j){
C[i][j] = (C[i-1][j] + C[i-1][j-1]) % P;
}
}
scanf("%d", &T);
while(T--){
scanf("%d%d%d%d", &n, &m, &k, &v);
for(int i = 0; i <= n; ++ i){
for(int j = 0; j <= n + n; ++ j){
if(i == 0){
F[i][j] = mihe(v, i + j);
} else {
F[i][j] = (1ll * (v + 1) * F[i-1][j] - F[i-1][j+1] + P) % P;
}
}
}
ll sub = 0;
for(int i = 1; i <= k; ++ i){
for(int j = 1; j <= n - k; ++ j){
if((i + j) & 1){
sub = (sub - 1ll * C[k][i] * C[n-k][j] % P * qp(F[k-i][n-k-j], m) % P + P) % P;
} else {
sub = (sub + 1ll * C[k][i] * C[n-k][j] % P * qp(F[k-i][n-k-j], m)) % P;
}
}
}
ll ans = F[k][n-k];
for(int i = 0; i <= k; ++ i){
for(int j = 0; j <= n; ++ j){
if(i == 0){
F[i][j] = mihe(v - 1, i + j);
} else {
F[i][j] = (1ll * v * F[i-1][j] - F[i-1][j+1] + P) % P;
}
}
}
ans = (ans - F[k][n-k] + P + P) % P;
ans = qp(ans, m);
printf("%lld\n", (ans - sub + P) % P * C[n][k] % P);
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号