2024.04 别急记录
1. 餐巾计划问题
建图跑费用流即可:
- \((S,1,\inf,p)\);
- \(\forall i\in[1,N],(i,i+N,r_i,0)\);
- \(\forall i\in[1,N],(S,i+N,r_i,0)\);
- \(\forall i\in[1,N],(i,T,r_i,0)\);
- \(\forall i\in[1,N),(i,i+1,\inf,0)\);
- \(\forall i\in[1,N-n],(i+N,i+n,\inf,f)\);
- \(\forall i\in[1,N-m],(i+N,i+m,\inf,s)\);
解释一下 234:
考虑把餐巾作为流,费用作为费用。则我们需要保证最大流为 \(\sum r\)。所以每个点要拆成两部分,表示干净毛巾和脏毛巾,再用脏毛巾的点流向洗过后的干净毛巾点。
点击查看代码
//P1251
#include <bits/stdc++.h>
using namespace std; typedef long long ll;
void solve();int main(){ solve(); return 0; }
const int N = 4e3 + 10, M = 4e4 + 10;
const ll inf = 1e10;
int n, r[N], p, u, f, v, s;
ll mc, ln[M], cs[M], ds[N];
int hd[N], eg[M], nx[M], tot = 1, nw[N], vs[N];
void adg(int u, int v, ll w, ll c){
eg[++tot] = v;
ln[tot] = w;
cs[tot] = c;
nx[tot] = hd[u];
hd[u] = tot;
}
void add(int u, int v, ll w, ll c){
// printf("%d %d %lld %lld\n", u, v, w, c);
adg(u, v, w, c);
adg(v, u, 0, -c);
}
bool spfa(int s, int t){
queue<int> q;
memset(ds, 0x3f, sizeof(ds));
memcpy(nw, hd, sizeof(hd));
q.push(s);
ds[s] = 0;
vs[s] = 1;
while(!q.empty()){
int x = q.front();
q.pop();
vs[x] = 0;
for(int i = hd[x]; i; i = nx[i]){
int y = eg[i];
ll z = ln[i], c = cs[i];
if(z && ds[y] > ds[x] + c){
ds[y] = ds[x] + c;
if(!vs[y]){
vs[y] = 1;
q.push(y);
}
}
}
}
return ds[t] != 0x3f3f3f3f3f3f3f3f;
}
ll dfs(int x, int t, ll fl){
if(x == t){
return fl;
}
ll rs = fl;
vs[x] = 1;
for(int i = nw[x]; i && rs; i = nx[i]){
int y = eg[i];
ll z = ln[i], c = cs[i];
nw[x] = i;
if(!vs[y] && z && ds[y] == ds[x] + c){
ll k = dfs(y, t, min(rs, z));
if(!k){
ds[y] = 0;
}
ln[i] -= k;
ln[i^1] += k;
rs -= k;
mc += k * c;
}
}
vs[x] = 0;
return fl - rs;
}
void solve(){
scanf("%d", &n);
for(int i = 1; i <= n; ++ i){
scanf("%d", &r[i]);
}
scanf("%d%d%d%d%d", &p, &u, &f, &v, &s);
int st = n + n + 1, ed = n + n + 2;
for(int i = 1; i <= n; ++ i){
add(i, i+n, r[i], 0);
add(st, i+n, r[i], 0);
add(i, ed, r[i], 0);
if(i < n){
add(i, i+1, inf, 0);
}
if(i + v <= n){
add(i+n, i+v, inf, s);
}
if(i + u <= n){
add(i+n, i+u, inf, f);
}
}
add(st, 1, inf, p);
while(spfa(st, ed)){
while(dfs(st, ed, inf*2));
}
printf("%lld\n", mc);
}
2. 国家集训队 - happiness
考虑答案=总和-最小割。
对于点 \(i\),连接 \((S,i),(i,T)\) 表示文和理,割掉表示不选。
对于额外贡献 \((i,j,p)\),若为文则新建点 \(x\) 连 \((S,x,p),(x,i,\inf),(x,j,\inf)\),否则连 \((i,x,\inf),(j,x,\inf),(x,T,p)\)。
点击查看代码
//P1646
#include <bits/stdc++.h>
using namespace std;
const int N = 5e4 + 10, inf = 100000, M = 3e5 + 10;
int n, m, hd[N], eg[M], ln[M], nx[M], tot = 1, now[N], dep[N];
void adg(int u, int v, int w){
eg[++tot] = v;
ln[tot] = w;
nx[tot] = hd[u];
hd[u] = tot;
}
void add(int u, int v, int w){
adg(u, v, w);
adg(v, u, 0);
}
bool bfs(int s, int t){
queue<int> q;
q.push(s);
memcpy(now, hd, sizeof(hd));
memset(dep, 0, sizeof(dep));
dep[s] = 1;
while(!q.empty()){
int x = q.front();
q.pop();
for(int i = hd[x]; i; i = nx[i]){
int y = eg[i], z = ln[i];
if(z && !dep[y]){
dep[y] = dep[x] + 1;
q.push(y);
if(y == t){
return 1;
}
}
}
}
return 0;
}
int dfs(int x, int t, int fl){
if(x == t){
return fl;
} else {
int rs = fl;
for(int i = now[x]; i && rs; i = nx[i]){
int y = eg[i], z = ln[i];
now[x] = i;
if(z && dep[y] == dep[x] + 1){
int k = dfs(y, t, min(rs, z));
if(!k){
dep[y] = 0;
}
ln[i] -= k;
ln[i^1] += k;
rs -= k;
}
}
return fl - rs;
}
}
int main(){
#define cg(x, y) ((x - 1) * m + y)
scanf("%d%d", &n, &m);
int sm = 0;
int st = cg(n, m) + 1, ed = cg(n, m) + 2, a, cnt = cg(n, m) + 2;
for(int i = 1; i <= n; ++ i){
for(int j = 1; j <= m; ++ j){
scanf("%d", &a);
sm += a;
add(st, cg(i, j), a);
}
}
for(int i = 1; i <= n; ++ i){
for(int j = 1; j <= m; ++ j){
scanf("%d", &a);
sm += a;
add(cg(i, j), ed, a);
}
}
for(int i = 1; i < n; ++ i){
for(int j = 1; j <= m; ++ j){
scanf("%d", &a);
sm += a;
++ cnt;
add(st, cnt, a);
add(cnt, cg(i, j), inf);
add(cnt, cg(i+1, j), inf);
}
}
for(int i = 1; i < n; ++ i){
for(int j = 1; j <= m; ++ j){
scanf("%d", &a);
sm += a;
++ cnt;
add(cnt, ed, a);
add(cg(i, j), cnt, inf);
add(cg(i+1, j), cnt, inf);
}
}
for(int i = 1; i <= n; ++ i){
for(int j = 1; j < m; ++ j){
scanf("%d", &a);
sm += a;
++ cnt;
add(st, cnt, a);
add(cnt, cg(i, j), inf);
add(cnt, cg(i, j+1), inf);
}
}
for(int i = 1; i <= n; ++ i){
for(int j = 1; j < m; ++ j){
scanf("%d", &a);
sm += a;
++ cnt;
add(cnt, ed, a);
add(cg(i, j), cnt, inf);
add(cg(i, j+1), cnt, inf);
}
}
int mf = 0, tmp;
while(bfs(st, ed)){
while(tmp = dfs(st, ed, inf)) mf += tmp;
}
printf("%d\n", sm - mf);
return 0;
}
3. qoj1427 - Flip
考虑 \(\sum k=2*10^5\) 的话不同 \(k\) 只有根号个,而相同 \(k\) 之间可以直接算。
然后 \(k\geq450\) 的也只有根号个,可以根号分治。
两个部分分别都可以根号做。
点击查看代码
//qoj1427
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll P = 998244353;
const int N = 2e5 + 10;
int n, m, c, a[N];
ll fac[N], inv[N], pw[N], ivy, ans[N];
vector<pair<int, int> > g[N], h[N];
ll qp(ll x, ll y){
ll ans = 1;
while(y){
if(y & 1){
ans = ans * x % P;
}
x = x * x % P;
y >>= 1;
}
return ans;
}
ll C(int x, int y){
if(x < y) return 0;
return fac[x] * inv[y] % P * inv[x-y] % P;
}
int main(){
fac[0] = pw[0] = 1;
for(int i = 1; i < N; ++ i){
fac[i] = fac[i-1] * i % P;
pw[i] = pw[i-1] * 2 % P;
}
inv[N-1] = qp(fac[N-1], P-2);
for(int i = N - 2; i >= 0; -- i){
inv[i] = inv[i+1] * (i+1) % P;
}
scanf("%d%d", &n, &m);
ivy = qp(pw[n+n], P-2);
for(int cs = 1; cs <= m; ++ cs){
scanf("%d", &c);
for(int i = 1; i <= c; ++ i){
scanf("%d", &a[i]);
}
if(a[c] < n + n){
ans[cs] = (ans[cs] + C(a[c]-c, n-c) * pw[n+n-a[c]]) % P;
}
g[c].push_back(make_pair(max(n, a[c]+1), cs));
int ls = n - 1;
if(c > 450){
for(int i = 1; i <= c; ++ i){
if(a[i] > ls){
for(int k = ls+1; k < a[i]; ++ k){
ans[cs] = (ans[cs] + C(k-i, n-1) * pw[n+n-k]) % P;
}
ls = a[i];
}
}
h[c+1].push_back(make_pair(ls+1, cs));
h[c+1].push_back(make_pair(n+n, -cs));
} else {
for(int i = 1; i <= c; ++ i){
if(a[i] > ls){
h[i].push_back(make_pair(ls+1, cs));
h[i].push_back(make_pair(a[i], -cs));
ls = a[i];
}
}
h[c+1].push_back(make_pair(ls+1, cs));
h[c+1].push_back(make_pair(n+n, -cs));
}
}
for(int i = 1; i <= n; ++ i){
if(g[i].size()){
sort(g[i].begin(), g[i].end());
reverse(g[i].begin(), g[i].end());
int nw = n + n;
ll rs = 0;
for(auto j : g[i]){
while(nw > j.first){
-- nw;
rs = (rs + C(nw-1-i, n-1-i) * pw[n+n-nw]) % P;
}
ans[j.second] = (ans[j.second] + rs) % P;
}
}
}
for(int i = 1; i <= n + 1; ++ i){
if(h[i].size()){
sort(h[i].begin(), h[i].end());
reverse(h[i].begin(), h[i].end());
int nw = n + n;
ll rs = 0;
for(auto j : h[i]){
while(nw > j.first){
-- nw;
rs = (rs + C(nw-i, n-1) * pw[n+n-nw]) % P;
}
if(j.second > 0){
ans[j.second] = (ans[j.second] + rs) % P;
} else {
ans[-j.second] = (ans[-j.second] - rs + P) % P;
}
}
}
}
for(int i = 1; i <= m; ++ i){
printf("%lld\n", 2 * ans[i] * ivy % P);
}
return 0;
}
4. USACO 2024 OPEN - Cowreography G
考虑第一个串中 '1' 的位置为 \(x_1,x_2,...,x_k\),第二个串中为 \(y_1,y_2,...,y_k\),则我们可以对这 \(k\) 对进行匹配,一对 \(x,y\) 的代价为 \(\lceil\dfrac{|y-x|}k\rceil\) 考虑后面的去匹配前面的。则从左往右遍历,维护两个集合表示 '1' 在上面的串还是下面的,那么对于位置 \(i\),优先找的位置为与 \(i\) 模 \(k\) 同余的,其次找模 \(k\) 余数比 \(i\) 模 \(k\) 大 \(1\) 的,以此类推。
点击查看代码
//P10280
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int n, k;
char s[N], t[N];
long long ans;
set<pair<int, int> > st[2];
int main(){
scanf("%d%d", &n, &k);
scanf("%s%s", s+1, t+1);
for(int i = 1; i <= n; ++ i){
if(s[i] != t[i]){
int x = s[i] - '0';
if(st[!x].empty()){
st[x].insert(make_pair(i%k, i));
} else {
auto it = st[!x].lower_bound(make_pair(i % k, 0));
if(it == st[!x].end()){
it = st[!x].begin();
}
ans += (i - (*it).second - 1) / k + 1;
st[!x].erase(it);
}
}
}
printf("%lld\n", ans);
return 0;
}
5. CCO2019 - Sirtet
首先 dfs 出所有连通块。对于一个连通块 \(X\),可以定义一个变量 \(d_{X}\) 表示下落后连通块 \(X\) 最低点在哪一行。预处理出连通块中每个点 \((i,j)\) 比它所在连通块最低点高了 \(t_{(i,j)}\) 行,则每个点下落后的位置为 \(x-t_{(i,j)}+1\)。
对于两个连通块 \(A,B\),若 \((p,y)\in A,(q,y)\in B,p<q\),则我们可以得出 \(d_A-t_{(p,y)}+1<d_B-t_{(q,y)}+1\),是一个差分约束的形式。所以可以列出所有这样的限制后建图跑一遍差分约束即可。
由于建 \(0\) 边跑最短路差分约束所求的解是 \(\leq 0\) 的最大值,所以对于每个数 \(+n\) 即为最终的位置。
不卡 spfa 啊。
点击查看代码
//P5532
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5e6 + 10;
const int dx[4] = {0, -1, 1, 0}, dy[4] = {-1, 0, 0, 1};
int plv[N], pcl[N], vs[N], ds[N], n, m, cs;
vector<pair<int, int> > g[N];
char pl[N], ans[N];
void dfs(int x, int y, int l, int c){
char (&s)[n+3][m+3] = decltype(s)(pl);
int (&cl)[n+3][m+3] = decltype(cl)(pcl);
int (&lv)[n+3][m+3] = decltype(lv)(plv);
lv[x][y] = l;
cl[x][y] = c;
for(int i = 0; i < 4; ++ i){
int xx = x + dx[i], yy = y + dy[i];
if(s[xx][yy] == '#' && !lv[xx][yy]){
dfs(xx, yy, l-dx[i], c);
}
}
}
void spfa(int st){
queue<int> q;
memset(vs, 0, sizeof(vs));
memset(ds, 0x3f, sizeof(ds));
vs[st] = 1, ds[st] = 0, q.push(st);
while(!q.empty()){
int x = q.front();
q.pop();
vs[x] = 0;
for(auto i : g[x]){
if(ds[i.first] > ds[x] + i.second){
ds[i.first] = ds[x] + i.second;
if(!vs[i.first]){
q.push(i.first);
vs[i.first] = 1;
}
}
}
}
}
int main(){
scanf("%d%d", &n, &m);
char (&s)[n+3][m+3] = decltype(s)(pl);
char (&t)[n+3][m+3] = decltype(t)(ans);
int (&cl)[n+3][m+3] = decltype(cl)(pcl);
int (&lv)[n+3][m+3] = decltype(lv)(plv);
for(int i = 1; i <= n; ++ i){
scanf("%s", s[i] + 1);
}
for(int i = n; i >= 1; -- i){
for(int j = 1; j <= m; ++ j){
t[i][j] = '.';
if(!lv[i][j] && s[i][j] == '#'){
dfs(i, j, 1, ++ cs);
}
}
}
for(int j = 1; j <= m; ++ j){
int ls = 0;
for(int i = n; i >= 1; -- i){
if(s[i][j] != '#'){
continue;
}
if(ls && cl[i][j] != cl[ls][j]){
g[cl[ls][j]].emplace_back(cl[i][j], lv[i][j]-lv[ls][j]-1);
}
ls = i;
}
}
for(int i = 1; i <= cs; ++ i){
g[cs+1].emplace_back(i, 0);
}
spfa(cs + 1);
for(int i = 1; i <= n; ++ i){
for(int j = 1; j <= m; ++ j){
if(s[i][j] == '#'){
t[ds[cl[i][j]]+n-lv[i][j]+1][j] = '#';
}
}
}
for(int i = 1; i <= n; ++ i){
printf("%s\n", t[i] + 1);
}
return 0;
}
6. LuoguP3600 - 随机数生成器
水黑逆天 \(O(nx\log n)\) 做法!
考虑设 \(f_i\) 表示 \(\max\min\leq T\) 的方案数,则此时每个数可以分为 \(>T,\leq T\) 两部分,合法当且仅当每个区间内存在数 \(\leq T\)。可以 \(O(n^2)\) 做。然后使用线段树优化 dp 即可做到 \(O(nx\log n)\)。
点击查看代码
//P3600
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2010;
const ll P = 666623333;
int n, x, q, mr[N];
ll f[N][N], g[N];
ll qp(ll x, ll y){
ll ans = 1;
while(y){
if(y & 1){
ans = ans * x % P;
}
x = x * x % P;
y >>= 1;
}
return ans;
}
ll t[N*4], tag[N*4];
void psd(int p){
t[p<<1] = t[p<<1] * tag[p] % P;
t[p<<1|1] = t[p<<1|1] * tag[p] % P;
tag[p<<1] = tag[p<<1] * tag[p] % P;
tag[p<<1|1] = tag[p<<1|1] * tag[p] % P;
tag[p] = 1;
}
void mul(int p, int l, int r, int ql, int qr, ll v){
if(ql <= l && r <= qr){
t[p] = t[p] * v % P;
tag[p] = tag[p] * v % P;
} else if(r < ql || qr < l){
return;
} else {
int mid = l + r >> 1;
psd(p);
mul(p<<1, l, mid, ql, qr, v);
mul(p<<1|1, mid+1, r, ql, qr, v);
t[p] = (t[p<<1] + t[p<<1|1]) % P;
}
}
void add(int p, int l, int r, int x, ll v){
if(l == r){
t[p] = (t[p] + v) % P;
} else {
int mid = l + r >> 1;
psd(p);
if(x <= mid){
add(p<<1, l, mid, x, v);
} else {
add(p<<1|1, mid+1, r, x, v);
}
t[p] = (t[p<<1] + t[p<<1|1]) % P;
}
}
ll qry(int p, int l, int r, int ql, int qr){
if(ql <= l && r <= qr){
return t[p];
} else if(r < ql || qr < l){
return 0;
} else {
int mid = l + r >> 1;
psd(p);
return (qry(p<<1, l, mid, ql, qr) +
qry(p<<1|1, mid+1, r, ql, qr)) % P;
}
}
int main(){
scanf("%d%d%d", &n, &x, &q);
for(int i = 1; i <= q; ++ i){
int l, r;
scanf("%d%d", &l, &r);
mr[r] = max(mr[r], l);
}
for(int T = 1; T <= x; ++ T){
mul(1, 0, n, 0, n, 0);
add(1, 0, n, 0, 1);
for(int i = 1; i <= n; ++ i){
ll val = t[1] * T % P;
t[1] = t[1] * (x-T) % P;
tag[1] = tag[1] * (x-T) % P;
mul(1, 0, n, 0, mr[i]-1, 0);
add(1, 0, n, i, val);
}
g[T] = t[1];
}
ll ans = 0;
for(int i = n; i >= 1; -- i){
g[i] = (g[i] - g[i-1] + P) % P;
ans += g[i] * i % P;
ans %= P;
}
printf("%lld\n", ans * qp(qp(x, n), P-2) % P);
return 0;
}
7. AGC066A - Adjacent Difference
设 \(f(x)\) 表示与 \(x\) 最接近的为 \(d\) 奇数倍倍数的数;\(g(x)\) 表示与 \(x\) 最接近的为 \(d\) 偶数倍倍数的数,则容易发现有 \(|f(x)-g(x)|=d\) 且二者一个 \(\leq x\) 一个 \(\geq x\)。
考虑对矩阵黑白染色,相邻位置不同色,有两种末方案:
- 黑色位置取 \(f(x)\),白色位置取 \(g(x)\);
- 黑色位置取 \(g(x)\),白色位置取 \(f(x)\);
容易发现二者的代价和为 \(dn^2\),故存在一个代价 \(\leq \dfrac 12 dn^2\)。
点击查看代码
//AT_agc066_a
#include <bits/stdc++.h>
using namespace std; typedef long long ll;
void solve();int main(){ solve(); return 0; }
const int N = 510;
int n, d, a[N][N], b[N][N], c[N][N], sb, sc;
void solve(){
scanf("%d%d", &n, &d);
for(int i = 1; i <= n; ++ i){
for(int j = 1; j <= n; ++ j){
scanf("%d", &a[i][j]);
a[i][j] += 1000;
if(((i + j) & 1) ^ ((a[i][j] / d) & 1)){
b[i][j] = a[i][j] - a[i][j] % d;
c[i][j] = b[i][j] + d;
sb += a[i][j] - b[i][j];
sc += c[i][j] - a[i][j];
} else {
c[i][j] = a[i][j] - a[i][j] % d;
b[i][j] = c[i][j] + d;
sc += a[i][j] - c[i][j];
sb += b[i][j] - a[i][j];
}
}
}
for(int i = 1; i <= n; ++ i){
for(int j = 1; j <= n; ++ j){
printf("%d ", (sb < sc ? b[i][j] : c[i][j]) - 1000);
}
puts("");
}
}
8. AGC066B - Decreasing Digit Sums
考虑对于形如 \(5^k\) 的数,比如 \(125\to250\to500\to1000\),看似直接满足条件了,但是 \(5^k\) 的数位和并不是递增的,于是我们可以把 \(5^k,5^{k-1},...,5\) 拼起来,如 \(...3125625125255\),可以发现这个数多次 \(\times 2\) 会变成:
- \(...3,125,625,125,255\);
- \(...6,251,250,250,510\);
- \(...12,502,500,501,020\);
- \(...25,005,001,002,040\);
- \(...50,010,002,004,080\)。
假设最高位是 \(5^k\),那么每次操作后数位和相当于减少 \(f(5^{k-x})\),增加 \(f(2^x)\)(\(x\in[0,n]\))。当 \(k\) 尽可能大的时候更有可能成功。打表可得 \(k=160\) 时可行且总长度 \(<10000\)。
点击查看代码
//AT_agc066_b
#include <bits/stdc++.h>
using namespace std; typedef long long ll;
void solve();int main(){ solve(); return 0; }
const int N = 10010;
int s[N], t[N];
int n, len = 1, tot = 1;
void solve(){
cin >> n;
t[1] = s[1] = 5;
for(int i = 2; i <= 160; ++ i){
for(int j = 1; j <= len; ++ j){
t[j] = t[j] * 5;
t[j] = t[j] + t[j-1] / 10;
t[j-1] %= 10;
}
while(t[len] >= 10){
t[len+1] = t[len] / 10;
t[len] %= 10;
++ len;
}
for(int j = 1; j <= len; ++ j){
s[++tot] = t[j];
}
}
for(int i = tot; i >= 1; -- i){
printf("%d", s[i]);
}
puts("");
}
9. AGC066C - Delete AAB or BAA
一个结论:
若一个串能够被删空,当且仅当它满足以下两个条件,或它能拆分成若干个满足以下两个条件的子串:
A的数量为B的两倍。- 首尾中有一个是
B。
对于本身满足两个条件的串 \(S,|S|=3k\),考虑归纳证明:
- 若 \(k=1\),
AAB,BAA满足条件; - 找到一段长度 \(\geq 2\) 的极长
A段,它的两侧各为空或者一个B,容易发现至少有一个B不在两侧,删掉这个B以及相邻的两个A变成了 \(3(k-1)\) 的子问题且依旧满足条件 2。
而对于任意一个能够被删空的串,考虑从空串往中间插入,容易发现肯定也满足条件。
所以可以进行 dp。设 \(f_i\) 表示 \([1,i]\) 至少要保留几个字符,转移为 \(f_i=f_{i-1}+1\) 以及当 \((j,i]\) 满足条件时 \(f_i=f_j\)。
设 \(sum_i=\sum_{j\leq i}[S_j='A']1-[S_j='B']2,\),则第一个条件可以写成 \(sum_i=sum_j\)。
点击查看代码
//AT_agc066_c
#include <bits/stdc++.h>
using namespace std; typedef long long ll;
void solve();int main(){ solve(); return 0; }
const int N = 5e6 + 10;
int T, n, f[N], g[N], h[N];
char s[N];
void solve(){
scanf("%d", &T);
while(T--){
scanf("%s", s + 1);
n = strlen(s + 1);
int sum = N / 2;
for(int i = sum - n*2; i <= sum + n*2; ++ i){
g[i] = h[i] = 0x3f3f3f3f;
}
for(int i = 0; i <= n; ++ i){
if(i){
f[i] = f[i-1] + 1;
if(s[i] == 'A'){
++ sum;
f[i] = min(f[i], g[sum]);
} else {
-- sum;
-- sum;
f[i] = min(f[i], g[sum]);
f[i] = min(f[i], h[sum]);
}
}
if(s[i+1] == 'B'){
g[sum] = min(g[sum], f[i]);
} else {
h[sum] = min(h[sum], f[i]);
}
}
printf("%d\n", (n - f[n]) / 3);
for(int i = 0; i <= n; ++ i){
f[i] = 0;
}
}
}
10. CF526F - Pudding Monsters
考虑从左往右枚举右端点 \(r\),动态维护一棵线段树,位置 \(l\) 的值为 \(t_l=\max[l,r]-\min[l,r]+l\),那么若一个 \([l,r]\) 可行当且仅当 \(t_l=r\)。观察到 \(t_l\geq r\),所以只用求线段树上 \([1,r]\) 区间内最小值个数即可。
新增右端点 \(r\) 时,可以维护两个单调栈,在维护的同时更新 \(\max,\min\)。一棵支持区间加+区间最值个数查询的线段树即可维护。
点击查看代码
//CF526F
#include <bits/stdc++.h>
using namespace std; typedef long long ll;
void solve();int main(){ solve(); return 0; }
const int N = 3e5 + 10;
int n, a[N], mx[N], mn[N], tx, tn;
ll ans = 0;
struct node{
int tag, mn, cnt;
} t[N*4];
void psd(int p){
t[p<<1].tag += t[p].tag;
t[p<<1].mn += t[p].tag;
t[p<<1|1].tag += t[p].tag;
t[p<<1|1].mn += t[p].tag;
t[p].tag = 0;
}
void build(int p, int l, int r){
t[p].cnt = r - l + 1;
if(l == r){
return;
}
int mid = l + r >> 1;
build(p<<1, l, mid);
build(p<<1|1, mid+1, r);
}
void add(int p, int l, int r, int ql, int qr, int x){
if(qr < l || r < ql){
return;
} else if(ql <= l && r <= qr){
t[p].mn += x;
t[p].tag += x;
} else {
int mid = l + r >> 1;
psd(p);
add(p<<1, l, mid, ql, qr, x);
add(p<<1|1, mid+1, r, ql, qr, x);
t[p].mn = min(t[p<<1].mn, t[p<<1|1].mn);
if(t[p<<1].mn < t[p<<1|1].mn){
t[p].cnt = t[p<<1].cnt;
} else if(t[p<<1].mn > t[p<<1|1].mn){
t[p].cnt = t[p<<1|1].cnt;
} else {
t[p].cnt = t[p<<1].cnt + t[p<<1|1].cnt;
}
}
}
pair<int, int> qry(int p, int l, int r, int ql, int qr){
if(qr < l || r < ql){
return make_pair(1e9, 0);
} else if(ql <= l && r <= qr){
return make_pair(t[p].mn, t[p].cnt);
} else {
int mid = l + r >> 1;
psd(p);
pair<int, int> x = qry(p<<1, l, mid, ql, qr);
pair<int, int> y = qry(p<<1|1, mid+1, r, ql, qr);
if(x.first < y.first){
return x;
} else if(x.first > y.first){
return y;
} else {
return make_pair(x.first, x.second + y.second);
}
}
}
void solve(){
scanf("%d", &n);
for(int i = 1; i <= n; ++ i){
int x, y;
scanf("%d%d", &x, &y);
a[x] = y;
}
build(1, 1, n);
for(int i = 1; i <= n; ++ i){
add(1, 1, n, i, i, i);
while(tx && a[mx[tx]] < a[i]){
add(1, 1, n, mx[tx-1]+1, mx[tx], -a[mx[tx]]);
-- tx;
}
add(1, 1, n, mx[tx]+1, i, a[i]);
mx[++tx] = i;
while(tn && a[mn[tn]] > a[i]){
add(1, 1, n, mn[tn-1]+1, mn[tn], a[mn[tn]]);
-- tn;
}
add(1, 1, n, mn[tn]+1, i, -a[i]);
mn[++tn] = i;
ans += qry(1, 1, n, 1, i).second;
}
printf("%lld\n", ans);
}
11. NOI2023 - 贸易
一条路径 \((x,y)\) 可以拆分成 \((x,lca),(lca,y)\) 两部分。第一部分直接是树边权值和;第二部分可能是 \(lca\) 先向上若干格,走一条非树边到达子数中。可以首先处理这些非树边目标点 \(dis\) 然后跑一遍 dij 解决。
点击查看代码
//P9481
//You can get an NOI2023 Ag by solving this problem!
//You can get an NOI2023 Au by 509pts.
//You can get 5pts by O(3^n) 后面忘了
//509+5=514
//then 进入集训队!!!
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 262150;
const ll P = 998244353;
int n, m, a[N], dep[N], vis[N];
vector<pair<int, int> > g[N];
vector<int> eg[N], son[N];
ll sum[N], dis[N], ans, fa[N][20];
struct edge{
int u, v, w;
} e[N];
int main(){
scanf("%d%d", &n, &m);
n = (1 << n) - 1;
dep[1] = 1;
son[1].push_back(1);
for(int i = 2; i <= n; ++ i){
son[i].push_back(i);
scanf("%d", &a[i]);
dep[i] = dep[i>>1] + 1;
for(int j = 1; j <= dep[i]; ++ j){
fa[i][j] = fa[i][j-1] + a[i>>(j-1)];
sum[i>>j] = (sum[i>>j] + fa[i][j]) % P;
son[i>>j].push_back(i);
}
}
for(int i = 1; i <= m; ++ i){
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
e[i] = { u, v, w };
g[u].emplace_back(v, w);
int x = v;
while(x != u){
eg[x].push_back(i);
x >>= 1;
}
}
for(int rt = 1; rt <= n / 2; ++ rt){
priority_queue<pair<ll, int> > q;
for(int j : son[rt]){
dis[j] = 1e18;
vis[j] = 0;
}
dis[rt] = 0;
q.push(make_pair(-dis[rt], rt));
while(!q.empty()){
int x = q.top().second;
q.pop();
if(vis[x] == 1){
continue;
}
vis[x] = 1;
if(x == rt){
for(int i : eg[x]){
int y = e[i].v;
ll z = e[i].w;
z += fa[x][dep[x] - dep[e[i].u]];
if(dis[y] > dis[x] + z){
dis[y] = dis[x] + z;
q.push(make_pair(-dis[y], y));
}
}
}
for(auto i : g[x]){
int y = i.first;
ll z = i.second;
if(dis[y] > dis[x] + z){
dis[y] = dis[x] + z;
q.push(make_pair(-dis[y], y));
}
}
if((x>>1) >= rt && dis[x>>1] > dis[x] + a[x]){
dis[x>>1] = dis[x] + a[x];
q.push(make_pair(-dis[x>>1], x>>1));
}
}
ll le = 0, cle = 1;
for(int j : son[rt<<1]){
if(dis[j] > 1e16){
continue;
}
++ cle;
le = (le + dis[j]) % P;
}
ans = (ans + cle * (sum[rt<<1|1] + a[rt<<1|1] * son[rt<<1|1].size() % P)) % P;
ans = (ans + le * (son[rt<<1|1].size() + 1)) % P;
cle = 1, le = 0;
for(int j : son[rt<<1|1]){
if(dis[j] > 1e16){
continue;
}
++ cle;
le = (le + dis[j]) % P;
}
ans = (ans + cle * (sum[rt<<1] + a[rt<<1] * son[rt<<1].size() % P)) % P;
ans = (ans + le * (son[rt<<1].size() + 1)) % P;
}
printf("%lld\n", ans);
return 0;
}
12. THUPC 2024 初赛 - 多折较差验证
首先预处理 \(ok_{l,r}\) 表示 \([l,r]\) 可以被折空。显然有 \(O(n^3)\) 的转移。考虑 \(f_{l,r}\) 的最优折叠点一定是中点两侧离中点最近的两个合法折叠位置。于是预处理出这两个位置暴力转移即可 \(O(n^2)\)。
点击查看代码
//P9964
#include <bits/stdc++.h>
using namespace std;
const int N = 5010;
int n, f[N][N][2], ok[N][N], g[N][N][2];
char s[N];
int main(){
scanf("%d%s", &n, s+1);
for(int len = 1; len <= n; len += 2){
for(int l = 1; l + len - 1 <= n; ++ l){
int r = l + len - 1;
if(l == r){
ok[l][r] = 1;
} else {
ok[l][r] = (s[l] != s[r]) & ok[l+1][r-1];
}
if(ok[l][r]){
g[l][r][0] = g[l][r][1] = (l+r) >> 1;
}
}
}
memset(f, 0x3f, sizeof(f));
for(int i = 1; i <= n; ++ i){
for(int j = i; j <= n; ++ j){
if(g[i][j][0] == 0){
g[i][j][0] = g[i][j-1][0];
}
}
}
for(int i = n; i >= 1; -- i){
for(int j = i; j >= 1; -- j){
if(g[j][i][1] == 0){
g[j][i][1] = g[j+1][i][1];
}
}
}
for(int len = 1; len <= n; ++ len){
for(int l = 1; l + len - 1 <= n; ++ l){
int r = l + len - 1;
if(l == r){
f[l][r][0] = 1;
f[l][r][1] = 0;
} else {
int x = g[l][r][0], y = g[l][r][1];
if(f[x+1][r][0] + 1 < f[l][r][0]){
f[l][r][0] = f[x+1][r][0] + 1;
f[l][r][1] = f[x+1][r][1] + r + l - x - x;
} else if(f[x+1][r][0] + 1 == f[l][r][0]){
f[l][r][1] = min(f[l][r][1], f[x+1][r][1] + r + l - x - x);
}
if(f[l][y-1][0] + 1 < f[l][r][0]){
f[l][r][0] = f[l][y-1][0] + 1;
f[l][r][1] = f[l][y-1][1] + y + y - r - l;
} else if(f[l][y-1][0] + 1 == f[l][r][0]){
f[l][r][1] = min(f[l][r][1], f[l][y-1][1] + y + y - r - l);
}
}
}
}
printf("%d %d\n", f[1][n][0], f[1][n][1]);
return 0;
}
13. AGC035C - Skolem XOR Tree
显然 \(n=2^k\) 时无解。
其他情况如图构造:
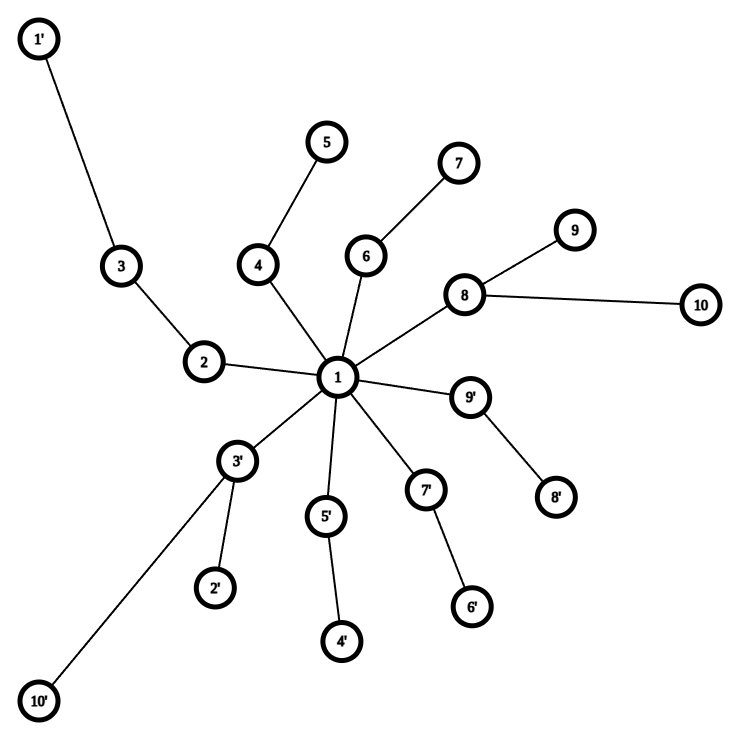
点击查看代码
//AT_agc035_c
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n;
int main(){
scanf("%d", &n);
int p = 1;
while(p < n){
p *= 2;
}
if(p == n){
puts("No");
} else {
puts("Yes");
printf("%d %d\n", 1+n, 3);
for(int i = 2; i <= n - 1; i += 2){
printf("%d %d\n", i, 1);
printf("%d %d\n", i, i+1);
printf("%d %d\n", i+n+1, 1);
printf("%d %d\n", i+n+1, i+n);
}
if(n % 2 == 0){
printf("%d %d\n", n, n-2);
printf("%d %d\n", n+n, n+(n^(n-2)^1));
}
}
return 0;
}
14. CF1874E - Jellyfish and Hack
首先可以设 \(f_{p,q}\) 表示长度为 \(p\),\(\operatorname{fun()}\) 值为 \(q\) 的排列个数,容易写出转移方程:
\(f_{p,q}=\sum\limits_{i=1}^p\dbinom{p-1}{i-1}\sum\limits_{j=0}^{q-p}f_{i-1,j}f_{p-i,q-p-j}\)。
设 \(F_p(x)=\sum\limits_{i=0}^{\infin}f_{p,q}x^q\),则有 \(F_p(x)=x^p\sum\limits_{i=1}^p\dbinom{p-1}{i-1}F_{i-1}(x)F_{p-i}(x)\)。
设 \(m=\dfrac{n(n+1)}2+1\)。
观察到若 \(2q>p(p+1)\),则 \(f_{p,q}=0\)。所以 \(F_n\) 至多 \(m-1\) 次。可以使用上述转移式计算出 \(F_n(1),F_n(2),...,F_n(m)\) 的值。
接下来可以倒着用拉格朗日插值,已知点值求出表达式。设 \(x_i=i,y_i=F_n(i)\)。
\(y=\sum\limits_{i=1}^my_i\prod\limits_{j\neq i}\dfrac 1{x_i-x_j}[\prod\limits_j(x-x_j)\dfrac1{x-x_i}]\)
枚举 \(i\),中括号以外的直接预处理;以内的可以先预处理出 \(\prod\limits_j(x-x_j)\) 再使用竖式除法除掉 \(x-x_i\)。
总复杂度 \(O(m^2)=O(n^4)\)。
点击查看代码
//CF1874E
#include <bits/stdc++.h>
using namespace std; typedef long long ll;
void solve();int main(){ solve(); return 0; }
const int N = 210;
const ll P = 1e9 + 7;
ll y[N*N], C[N][N], F[N];
ll fac[N*N], f[N*N], p[N*N], q[N*N];
int n, lim, m;
ll qp(ll x, ll y){
ll ans = 1;
while(y){
if(y & 1){
ans = ans * x % P;
}
x = x * x % P;
y >>= 1;
}
return ans;
}
void solve(){
cin >> n >> lim;
m = n * (n + 1) / 2 + 1;
for(int i = 0; i <= n; ++ i){
C[i][0] = C[i][i] = 1;
for(int j = 1; j < i; ++ j){
C[i][j] = (C[i-1][j] + C[i-1][j-1]) % P;
}
}
fac[0] = 1;
for(int i = 1; i <= m; ++ i){
fac[i] = fac[i-1] * i % P;
F[0] = 1;
ll pw = 1;
for(int k = 1; k <= n; ++ k){
pw = pw * i % P;
F[k] = 0;
for(int j = 1; j <= k; ++ j){
F[k] = (F[k] + C[k-1][j-1] * F[j-1] % P * F[k-j]) % P;
}
F[k] = F[k] * pw % P;
}
y[i] = F[n];
}
p[0] = 1;
for(int i = 1; i <= m; ++ i){
for(int j = 1; j <= i; ++ j){
q[j] = p[j-1];
p[j-1] = p[j-1] * (P - i) % P;
}
for(int j = 0; j <= i; ++ j){
p[j] = (p[j] + q[j]) % P;
}
}
for(int i = 1; i <= m; ++ i){
ll val = y[i] * qp(fac[i-1], P-2) % P * qp(fac[m-i], P-2) % P;
if((m - i) & 1){
val = P - val;
}
for(int j = 0; j <= m; ++ j){
q[j] = p[j];
}
for(int j = m - 1; j >= 0; -- j){
ll r = q[j+1];
f[j] = (f[j] + r * val) % P;
q[j] = (q[j] + r * i) % P;
}
}
ll ans = 0;
for(int i = lim; i < m; ++ i){
ans = (ans + f[i]) % P;
}
cout << ans << '\n';
}
15. AGC030C - Coloring Torus
这你都不会?
首先 \(k\leq 500\) 是平凡的。令 \(a_{x,i}=x\) 即可。
对于 \(k > 500\) 的情况,可以对于前 \(500\) 个数,把一个数 \(i\) 填到 \(a_{1,i},a_{2,i+1},...,a_{500,i-1}\) 中;若 \(i+500\leq k\),则把奇数行的 \(i\) 换成 \(500+i\)。
点击查看代码
//AT_agc030_c
#include <bits/stdc++.h>
using namespace std; typedef long long ll;
void solve();int main(){ solve(); return 0; }
const int N = 510;
int k, a[N][N];
void solve(){
// freopen(".out", "w", stdout);
scanf("%d", &k);
if(k <= 500){
printf("%d\n", k);
for(int i = 1; i <= k; ++ i){
for(int j = 1; j <= k; ++ j){
printf("%d ", j);
}
puts("");
}
} else {
puts("500");
for(int i = 1; i <= 500; ++ i){
for(int j = 1, p = i; j <= 500; ++ j){
a[j][p] = i;
if(i + 500 <= k && j % 2 == 0){
a[j][p] = i + 500;
}
++ p;
if(p > 500){
p -= 500;
}
}
}
for(int i = 1; i <= 500; ++ i){
for(int j = 1; j <= 500; ++ j){
printf("%d ", a[i][j]);
}
puts("");
}
}
}
16. NOI2020 - 超现实树

离正解就差一点/ll。
结论:若一棵树中存在一个节点的两个子结点均有子结点,则这棵树无效。
结论成立,因为这些数不会对任何其中一个儿子为空/其中一个儿子为叶子的树产生贡献。
有了这个结论然后使用四叉 trie 维护其中一个儿子为空/其中一个儿子为叶子共四种情况。然后从叶子往根 dp 一下即可。
点击查看代码
//P6776
#include <bits/stdc++.h>
using namespace std;
const int N = 2e6 + 10;
int T, m, n;
vector<pair<int, int> > g[N];
int ch[N][4], tot = 1, ok[N];
int sc(pair<int, int> x){
return (x.first ? 1 : 0) + (x.second ? 1 : 0);
}
void dfs(int i, int p, int q){
if(g[i][q].first && g[i][q].second){
if(!sc(g[i][g[i][q].first])){
if(!ch[p][2]) ch[p][2] = ++ tot;
dfs(i, ch[p][2], g[i][q].second);
}
if(!sc(g[i][g[i][q].second])){
if(!ch[p][3]) ch[p][3] = ++ tot;
dfs(i, ch[p][3], g[i][q].first);
}
} else if(g[i][q].first){
if(!ch[p][0]) ch[p][0] = ++ tot;
dfs(i, ch[p][0], g[i][q].first);
} else if(g[i][q].second){
if(!ch[p][1]) ch[p][1] = ++ tot;
dfs(i, ch[p][1], g[i][q].second);
} else {
ok[p] = 1;
}
}
int main(){
scanf("%d", &T);
while(T--){
scanf("%d", &m);
for(int i = 1; i <= m; ++ i){
scanf("%d", &n);
g[i].resize(n + 1);
for(int j = 1; j <= n; ++ j){
scanf("%d%d", &g[i][j].first, &g[i][j].second);
}
bool flg = 1;
for(int j = 1; j <= n; ++ j){
if(sc(g[i][g[i][j].first]) && sc(g[i][g[i][j].second])){
flg = 0;
break;
}
}
if(flg){
dfs(i, 1, 1);
}
}
for(int i = tot; i >= 1; -- i){
if(ok[ch[i][0]] && ok[ch[i][1]] && ok[ch[i][2]] && ok[ch[i][3]]){
ok[i] = 1;
}
}
puts(ok[1] ? "Almost Complete" : "No");
for(int i = 0; i <= tot; ++ i){
ch[i][0] = ch[i][1] = ch[i][2] = ch[i][3] = ok[i] = 0;
}
tot = 1;
}
return 0;
}
17. NOI2020 - 制作菜品
显然当 \(m\geq n-1\) 时可以直接贪心:取最小的和最大的中的一部分,转化为 $(n-1,m-1) $ 的问题。
当 \(m=n-2\) 时,考虑对于每个物品的两部分连一条边建图,则图不连通,即可以拆分成两个小问题,小问题中分别 \(m=n-1\)。使用背包求一下划分方案即可。
点击查看代码
//P6775
#include <bits/stdc++.h>
using namespace std;
const int N = 510;
int T, n, m, k, ok[N];
pair<int, int> d[N], p[N];
bitset<N*N*20> b[N];
void solve(int cnt, int l, int r){
int tp = l;
for(int i = 1; i <= cnt; ++ i){
sort(d + tp, d + r + 1);
if(d[tp].first > k){
printf("%d %d", d[tp].second, k);
d[tp].first -= k;
} else if(d[tp].first == k){
printf("%d %d", d[tp].second, k);
d[tp].first = 0;
++ tp;
} else {
printf("%d %d ", d[tp].second, d[tp].first);
printf("%d %d", d[r].second, k - d[tp].first);
d[r].first -= (k - d[tp].first);
d[tp].first = 0;
++ tp;
}
puts("");
}
}
int main(){
scanf("%d", &T);
while(T--){
scanf("%d%d%d", &n, &m, &k);
for(int i = 1; i <= n; ++ i){
scanf("%d", &d[i].first);
d[i].second = i;
}
if(m >= n - 1){
solve(m, 1, n);
} else {
int tmp = n * k + 3;
b[0].reset();
b[0].set(tmp);
for(int i = 1; i <= n; ++ i){
if(d[i].first >= k){
b[i] = b[i-1] | (b[i-1] << d[i].first - k);
} else {
b[i] = b[i-1] | (b[i-1] >> k - d[i].first);
}
}
if(b[n].test(tmp - k)){
int flg = tmp - k;
int l = 0, r = 0;
for(int i = n; i >= 1; -- i){
if(b[i-1].test(flg)){
continue;
}
for(int j = 1; j <= n; ++ j){
if(!ok[i] && b[i-1].test(flg-d[i].first+k)){
ok[i] = 1;
flg -= d[i].first-k;
++ r;
}
}
}
for(int i = 1; i <= n; ++ i){
if(ok[i] == 1){
p[++l] = d[i];
} else {
p[++r] = d[i];
}
ok[i] = 0;
}
memcpy(d, p, sizeof(p));
solve(l-1, 1, l);
solve(r-l-1, l+1, r);
} else {
puts("-1");
}
}
}
return 0;
}
18. LuoguP2633 - Count on a tree
使用主席树维护每个节点到根的值域线段树,接着使用类似树上差分的方法查询即可。
点击查看代码
//P2633
#include <bits/stdc++.h>
using namespace std; typedef long long ll;
void solve();int main(){ solve(); return 0; }
const int N = 1e5 + 10;
int n, m, rg, a[N], b[N], anc[N][20], dep[N];
int t[N*20], ls[N*20], rs[N*20], rt[N], cnt = 1;
vector<int> g[N];
int add(int p, int l, int r, int x){
int nw = ++ cnt;
tie(t[nw], ls[nw], rs[nw]) = tie(t[p], ls[p], rs[p]);
if(l == r){
++ t[nw];
} else {
int mid = l + r >> 1;
if(x <= mid){
ls[nw] = add(ls[nw], l, mid, x);
} else {
rs[nw] = add(rs[nw], mid+1, r, x);
}
t[nw] = t[ls[nw]] + t[rs[nw]];
}
return nw;
}
int qry(int p, int q, int x, int y, int l, int r, int k){
if(l == r){
return l;
} else {
int mid = l + r >> 1;
int val = t[ls[p]] + t[ls[q]] - t[ls[x]] - t[ls[y]];
if(val >= k){
return qry(ls[p], ls[q], ls[x], ls[y], l, mid, k);
} else {
return qry(rs[p], rs[q], rs[x], rs[y], mid+1, r, k-val);
}
}
}
void dfs(int x, int fa){
anc[x][0] = fa;
dep[x] = dep[fa] + 1;
rt[x] = add(rt[fa], 1, rg, a[x]);
for(int i = 1; i < 20; ++ i){
anc[x][i] = anc[anc[x][i-1]][i-1];
}
for(int i : g[x]){
if(i != fa){
dfs(i, x);
}
}
}
int lca(int x, int y){
if(dep[x] < dep[y]){
swap(x, y);
}
for(int i = 19; i >= 0; -- i){
if(dep[anc[x][i]] >= dep[y]){
x = anc[x][i];
}
}
if(x == y){
return x;
}
for(int i = 19; i >= 0; -- i){
if(anc[x][i] != anc[y][i]){
x = anc[x][i];
y = anc[y][i];
}
}
return anc[x][0];
}
void solve(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++ i){
scanf("%d", &a[i]);
b[i] = a[i];
}
sort(b + 1, b + n + 1);
rg = unique(b + 1, b + n + 1) - b - 1;
for(int i = 1; i <= n; ++ i){
a[i] = lower_bound(b + 1, b + rg + 1, a[i]) - b;
}
for(int i = 1; i < n; ++ i){
int x, y;
scanf("%d%d", &x, &y);
g[x].push_back(y);
g[y].push_back(x);
}
rt[0] = ++ cnt;
dfs(1, 0);
int ls = 0;
while(m--){
int u, v, k;
scanf("%d%d%d", &u, &v, &k);
u ^= ls;
int p = lca(u, v);
ls = b[qry(rt[u], rt[v], rt[p], rt[anc[p][0]], 1, rg, k)];
printf("%d\n", ls);
}
}
19. 国家集训队 - middle
考虑二分答案。让序列中的 \(a_i\) 变为 \((-1)[a_i<mid]+(1)[a_i\geq mid]\),则一个区间中位数 \(\geq mid\) 当且仅当 \(sum\geq 0\)。
于是我们可以使用两棵主席树,分别维护当 \(mid=k\) 时序列前缀和/后缀和。使用\(rt_{k-1}\) 推 \(rt_k\) 只需区间加操作即可。
查询时则对于二分到的每个 \(mid\),查询左端点在 \([a,b]\) 之间最大后缀、右端点在 \([c,d]\) 之间最大前缀即可。
点击查看代码
//P2839
#include <bits/stdc++.h>
using namespace std; typedef long long ll;
void solve();int main(){ solve(); return 0; }
const int N = 20010, M = 400;
int lrt[N], rrt[N], t[N*M], tag[N*M], ls[N*M], rs[N*M], cnt;
int n, a[N], q, la, pos[N];
pair<int, int> b[N];
int build(int l, int r, int op){
int p = ++ cnt;
if(l == r){
t[p] = op ? l : n - l + 1;
} else {
int mid = l + r >> 1;
ls[p] = build(l, mid, op);
rs[p] = build(mid+1, r, op);
t[p] = max(t[ls[p]], t[rs[p]]);
}
return p;
}
int nnd(int p){
++ cnt;
tie(t[cnt], tag[cnt], ls[cnt], rs[cnt]) = tie(t[p], tag[p], ls[p], rs[p]);
return cnt;
}
void psd(int p){
if(!tag[p]){
return;
}
ls[p] = nnd(ls[p]);
rs[p] = nnd(rs[p]);
tag[ls[p]] += tag[p];
tag[rs[p]] += tag[p];
t[ls[p]] += tag[p];
t[rs[p]] += tag[p];
tag[p] = 0;
}
int add(int p, int l, int r, int ql, int qr){
p = nnd(p);
if(ql <= l && r <= qr){
tag[p] -= 2;
t[p] -= 2;
} else {
int mid = l + r >> 1;
psd(p);
if(ql <= mid){
ls[p] = add(ls[p], l, mid, ql, qr);
}
if(mid < qr){
rs[p] = add(rs[p], mid+1, r, ql, qr);
}
t[p] = max(t[ls[p]], t[rs[p]]);
}
return p;
}
int ask(int p, int l, int r, int ql, int qr){
if(ql <= l && r <= qr){
return t[p];
} else {
int mid = l + r >> 1;
psd(p);
int ans = -2e9;
if(ql <= mid){
ans = max(ans, ask(ls[p], l, mid, ql, qr));
}
if(mid < qr){
ans = max(ans, ask(rs[p], mid+1, r, ql, qr));
}
return ans;
}
}
bool chk(int a, int b, int c, int d, int k){
-- k;
int val = 0;
val += ask(lrt[k], 1, n, c, d) - ask(lrt[k], 1, n, b, b);
val += ask(rrt[k], 1, n, a, b) - ask(rrt[k], 1, n, b+1, b+1);
return val >= 0;
}
void solve(){
scanf("%d", &n);
for(int i = 1; i <= n; ++ i){
scanf("%d", &a[i]);
b[i] = make_pair(a[i], i);
}
sort(b + 1, b + n + 1);
for(int i = 1; i <= n; ++ i){
a[i] = lower_bound(b + 1, b + n + 1, make_pair(a[i], i)) - b;
pos[a[i]] = i;
}
lrt[0] = build(1, n, 1);
rrt[0] = build(1, n, 0);
for(int i = 1; i <= n; ++ i){
lrt[i] = add(lrt[i-1], 1, n, pos[i], n);
rrt[i] = add(rrt[i-1], 1, n, 1, pos[i]);
}
scanf("%d", &q);
while(q--){
int p[4];
scanf("%d%d%d%d", &p[0], &p[1], &p[2], &p[3]);
p[0] = (p[0] + la) % n;
p[1] = (p[1] + la) % n;
p[2] = (p[2] + la) % n;
p[3] = (p[3] + la) % n;
sort(p, p + 4);
int l = 1, r = n;
while(l < r){
int mid = l + r + 1 >> 1;
if(chk(p[0] + 1, p[1] + 1, p[2] + 1, p[3] + 1, mid)){
l = mid;
} else {
r = mid - 1;
}
}
la = b[l].first;
printf("%d\n", la);
}
}
20. HEOI/TJOI2016 - 字符串
我都会,这不降紫?
问题相当于求最长的 \([c,d]\) 中前缀使得这个前缀是 \([a,b]\) 中的子串。求出 \(rk,height\) 数组。
考虑二分答案。设目前二分到 \(mid\),则与后缀 \([c,n]\) 的 \(lcp \geq mid\) 的串的 \(rk\) 为一个区间 \([x,y]\),可以使用二分+rmq 求出。
问题转化为 \(rk_{[a,b]}\) 中是否有 \(\in[x,y]\) 的数,是 IOI2018 狼人的套路,可以使用主席树做。
点击查看代码
//P4094
#include <bits/stdc++.h>
using namespace std; typedef long long ll;
void solve();int main(){ solve(); return 0; }
const int N = 1e5 + 10, M = 30;
int n, q;
int sa[N], rk[N], cnt[N], pre[N], h[N];
char s[N];
void suf(){
int m = 26;
for(int i = 1; i <= n; ++ i){
rk[i] = s[i] - 'a' + 1;
++ cnt[rk[i]];
}
for(int i = 2; i <= m; ++ i){
cnt[i] += cnt[i-1];
}
for(int i = n; i >= 1; -- i){
sa[cnt[rk[i]]--] = i;
}
for(int k = 1; k <= n; k <<= 1){
int tot = 0;
for(int i = n - k + 1; i <= n; ++ i){
pre[++tot] = i;
}
for(int i = 1; i <= n; ++ i){
if(sa[i] > k){
pre[++tot] = sa[i] - k;
}
}
for(int i = 1; i <= m; ++ i){
cnt[i] = 0;
}
for(int i = 1; i <= n; ++ i){
++ cnt[rk[i]];
}
for(int i = 2; i <= m; ++ i){
cnt[i] += cnt[i-1];
}
for(int i = n; i >= 1; -- i){
sa[cnt[rk[pre[i]]]--] = pre[i];
pre[i] = 0;
}
swap(rk, pre);
tot = 1, rk[sa[1]] = 1;
for(int i = 2; i <= n; ++ i){
if(pre[sa[i]] == pre[sa[i-1]] && pre[sa[i]+k] == pre[sa[i-1]+k]){
rk[sa[i]] = tot;
} else {
rk[sa[i]] = ++ tot;
}
}
if(tot == n){
break;
}
m = tot;
}
int k = 0;
for(int i = 1; i <= n; ++ i){
if(rk[i] == 1){
h[1] = 0;
}
if(k){
-- k;
}
int j = sa[rk[i]-1];
while(j+k <= n && i+k <= n && s[i+k] == s[j+k]){
++ k;
}
h[rk[i]] = k;
}
}
int st[N][20];
void table(){
for(int i = 1; i <= n; ++ i){
st[i][0] = h[i];
}
for(int i = 1; i < 20; ++ i){
for(int j = 1; j + (1 << i) - 1 <= n; ++ j){
st[j][i] = min(st[j][i-1], st[j+(1<<i-1)][i-1]);
}
}
}
int qry(int l, int r){
if(l == r){
return 1e9;
}
if(l > r){
swap(l, r);
}
++ l;
int k = 31 ^ __builtin_clz(r - l + 1);
return min(st[l][k], st[r-(1<<k)+1][k]);
}
int t[N*M], ls[N*M], rs[N*M], rt[N], tot;
int add(int p, int l, int r, int x){
++ tot;
tie(t[tot], ls[tot], rs[tot]) = tie(t[p], ls[p], rs[p]);
p = tot;
if(l == r){
++ t[p];
} else {
int mid = l + r >> 1;
if(x <= mid){
ls[p] = add(ls[p], l, mid, x);
} else {
rs[p] = add(rs[p], mid+1, r, x);
}
t[p] = t[ls[p]] + t[rs[p]];
}
return p;
}
int sum(int p, int q, int l, int r, int ql, int qr){
if(qr < l || r < ql){
return 0;
} else if(ql <= l && r <= qr){
return t[p] - t[q];
} else {
int mid = l + r >> 1;
return sum(ls[p], ls[q], l, mid, ql, qr) + sum(rs[p], rs[q], mid+1, r, ql, qr);
}
}
void seg(){
for(int i = 1; i <= n; ++ i){
rt[i] = add(rt[i-1], 1, n, rk[i]);
}
}
bool chk(int a, int b, int c, int d, int k){
int l = a, r = b - k + 1;
int x, y;
int L = 1, R = rk[c];
while(L < R){
int mid = L + R >> 1;
if(qry(mid, rk[c]) >= k){
R = mid;
} else {
L = mid + 1;
}
}
x = L;
L = rk[c], R = n;
while(L < R){
int mid = L + R + 1 >> 1;
if(qry(rk[c], mid) >= k){
L = mid;
} else {
R = mid - 1;
}
}
y = L;
return sum(rt[r], rt[l-1], 1, n, x, y);
}
void solve(){
scanf("%d%d", &n, &q);
scanf("%s", s + 1);
suf();
seg();
table();
while(q--){
int a, b, c, d;
scanf("%d%d%d%d", &a, &b, &c, &d);
int l = 0, r = min(d - c + 1, b - a + 1);
while(l < r){
int mid = l + r + 1 >> 1;
if(chk(a, b, c, d, mid)){
l = mid;
} else {
r = mid - 1;
}
}
printf("%d\n", l);
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号