BZOJ1018[SHOI2008]堵塞的交通——线段树
题目描述
有一天,由于某种穿越现象作用,你来到了传说中的小人国。小人国的布局非常奇特,整个国家的交通系统可
以被看成是一个2行C列的矩形网格,网格上的每个点代表一个城市,相邻的城市之间有一条道路,所以总共有2C个
城市和3C-2条道路。 小人国的交通状况非常槽糕。有的时候由于交通堵塞,两座城市之间的道路会变得不连通,
直到拥堵解决,道路才会恢复畅通。初来咋到的你决心毛遂自荐到交通部某份差事,部长听说你来自一个科技高度
发达的世界,喜出望外地要求你编写一个查询应答系统,以挽救已经病入膏肓的小人国交通系统。 小人国的交通
部将提供一些交通信息给你,你的任务是根据当前的交通情况回答查询的问题。交通信息可以分为以下几种格式:
Close r1 c1 r2 c2:相邻的两座城市(r1,c1)和(r2,c2)之间的道路被堵塞了;Open r1 c1 r2 c2:相邻的两座城
市(r1,c1)和(r2,c2)之间的道路被疏通了;Ask r1 c1 r2 c2:询问城市(r1,c1)和(r2,c2)是否连通。如果存在一
条路径使得这两条城市连通,则返回Y,否则返回N;
输入
第一行只有一个整数C,表示网格的列数。接下来若干行,每行为一条交通信息,以单独的一行“Exit”作为
结束。我们假设在一开始所有的道路都是堵塞的。我们保证 C小于等于100000,信息条数小于等于100000。
输出
对于每个查询,输出一个“Y”或“N”。
样例输入
2
Open 1 1 1 2
Open 1 2 2 2
Ask 1 1 2 2
Ask 2 1 2 2
Exit
Open 1 1 1 2
Open 1 2 2 2
Ask 1 1 2 2
Ask 2 1 2 2
Exit
样例输出
Y
N
N
线段树维护连通性经典题。
怎么用线段树维护连通性?
因为只有两行,那么我们对列来建线段树,每一列分为上端点和下端点。
对于线段树的一个点维护这个点所代表区间的左上端点(lu)、右上端点(ru)、左下端点(ld)、右下端点(rd)这四个点之间的连通性。
回溯时直接合并左右子树代表的区间的信息。
同时还要记录对于一列x与x+1列之间的连通性,这个在回溯合并时会用到。
修改分为两种:修改横边和修改竖边。
修改竖边直接递归找修改边对应的那一列,然后回溯更新沿途信息。
修改横边递归找到当前区间的mid等于横边左端点所在列x,修改x与x+1列之间的连通性再回溯更新沿途信息。
查询时将查询到的log个区间合并,然后判断查询点的连通性?
考虑这样一种特殊情况:
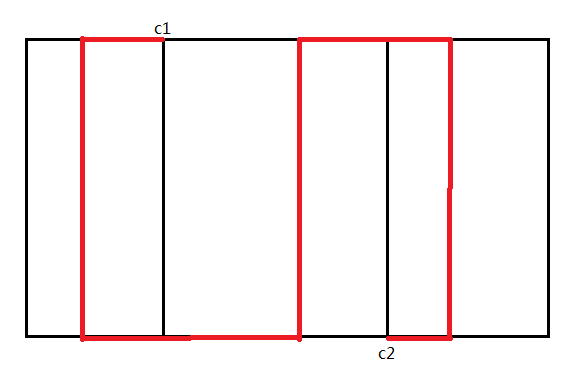
显然只查中间区间之后判断是不连通的,因此还要查[1,c1]和[c2,c]这两端的区间然后分情况讨论。
具体实现见代码,其中lu,ld,ru,rd为上述的区间四个端点。
#include<set>
#include<map>
#include<stack>
#include<queue>
#include<cmath>
#include<cstdio>
#include<vector>
#include<bitset>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
int t[100010][8];
int n;
char ch[10];
int a,b,c,d;
struct miku
{
int luld;
int rurd;
int lurd;
int ruld;
int luru;
int ldrd;
}s[800010];
void merge(miku &z,miku x,miku y,int mid)
{
z.luld=(x.luld)||(x.luru&&t[mid][1]&&y.luld&&t[mid][2]&&x.ldrd);
z.rurd=(y.rurd)||(y.luru&&t[mid][1]&&x.rurd&&t[mid][2]&&y.ldrd);
z.lurd=(x.lurd&&t[mid][2]&&y.ldrd)||(x.luru&&t[mid][1]&&y.lurd);
z.ruld=(x.ruld&&t[mid][1]&&y.luru)||(x.ldrd&&t[mid][2]&&y.ruld);
z.luru=(x.lurd&&t[mid][2]&&y.ruld)||(x.luru&&t[mid][1]&&y.luru);
z.ldrd=(x.ruld&&t[mid][1]&&y.lurd)||(x.ldrd&&t[mid][2]&&y.ldrd);
}
void build(int rt,int l,int r)
{
if(l==r)
{
s[rt].luru=1;
s[rt].ldrd=1;
return ;
}
int mid=(l+r)>>1;
build(rt<<1,l,mid);
build(rt<<1|1,mid+1,r);
merge(s[rt],s[rt<<1],s[rt<<1|1],mid);
}
void change1(int rt,int l,int r,int x,int k)
{
if(l==r)
{
s[rt].lurd=s[rt].ruld=s[rt].luld=s[rt].rurd=k;
return ;
}
int mid=(l+r)>>1;
if(x<=mid)
{
change1(rt<<1,l,mid,x,k);
}
else if(x>mid)
{
change1(rt<<1|1,mid+1,r,x,k);
}
merge(s[rt],s[rt<<1],s[rt<<1|1],mid);
}
void change2(int rt,int l,int r,int x,int y,int k)
{
int mid=(l+r)>>1;
if(x==mid)
{
t[x][y]=k;
merge(s[rt],s[rt<<1],s[rt<<1|1],mid);
return ;
}
if(x<=mid)
{
change2(rt<<1,l,mid,x,y,k);
}
else if(x>mid)
{
change2(rt<<1|1,mid+1,r,x,y,k);
}
merge(s[rt],s[rt<<1],s[rt<<1|1],mid);
}
miku query(int rt,int l,int r,int L,int R)
{
if(L<=l&&r<=R)
{
return s[rt];
}
int mid=(l+r)>>1;
if(R<=mid)
{
return query(rt<<1,l,mid,L,R);
}
if(L>mid)
{
return query(rt<<1|1,mid+1,r,L,R);
}
miku ans;
merge(ans,query(rt<<1,l,mid,L,R),query(rt<<1|1,mid+1,r,L,R),mid);
return ans;
}
int ask(int a,int b,int c,int d)
{
miku ls=query(1,1,n,1,b);
miku ms=query(1,1,n,b,d);
miku rs=query(1,1,n,d,n);
int t1,t2,t3,t4;
if(a==1&&c==1)
{
t1=ms.luru;
t2=(ls.rurd&&ms.ruld);
t3=(ms.lurd&&rs.luld);
t4=(ls.rurd&&ms.ldrd&&rs.luld);
if(t1||t2||t3||t4)
{
return 1;
}
else
{
return 0;
}
}
else if(a==1&&c==2)
{
t1=ms.lurd;
t2=(ls.rurd&&ms.ldrd);
t3=(ms.luru&&rs.luld);
t4=(ls.rurd&&ms.ruld&&rs.luld);
if(t1||t2||t3||t4)
{
return 1;
}
else
{
return 0;
}
}
else if(a==2&&c==1)
{
t1=ms.ruld;
t2=(ls.rurd&&ms.luru);
t3=(ms.ldrd&&rs.luld);
t4=(ls.rurd&&ms.lurd&&rs.luld);
if(t1||t2||t3||t4)
{
return 1;
}
else
{
return 0;
}
}
else if(a==2&&c==2)
{
t1=ms.ldrd;
t2=(ls.rurd&&ms.lurd);
t3=(ms.ruld&&rs.luld);
t4=(ls.rurd&&ms.luru&&rs.luld);
if(t1||t2||t3||t4)
{
return 1;
}
else
{
return 0;
}
}
}
int main()
{
scanf("%d",&n);
build(1,1,n);
while(1)
{
scanf("%s",ch);
if(ch[0]=='E')
{
break;
}
scanf("%d%d%d%d",&a,&b,&c,&d);
if(b>d)
{
swap(b,d);
swap(a,c);
}
if(ch[0]=='O')
{
if(a==c)
{
change2(1,1,n,b,a,1);
}
else
{
change1(1,1,n,b,1);
}
}
else if(ch[0]=='C')
{
if(a==c)
{
change2(1,1,n,b,a,0);
}
else
{
change1(1,1,n,b,0);
}
}
else
{
ask(a,b,c,d)==1?printf("Y\n"):printf("N\n");
}
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号