模拟赛SXJ202507300900题目

包包的自动售票机

问题描述

包包最近在\(C\) 市火车站发现了一台新式自动售票机，这台机器非常智能！当乘客输入目的地时，键盘会动态显示可选的字母，其他不可选的字母会被隐藏起来。包包对这种智能设计非常感兴趣，他想知道在输入部分字符后，键盘会变成什么样子。

在自动售票机屏幕上，有一个 \(4 \times 8\)的键盘，如下图所示。

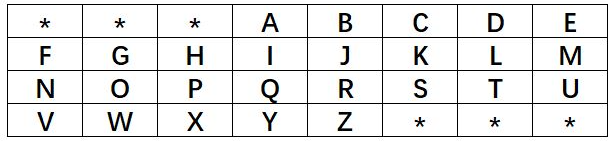
在乘客每输入一个字母后，键盘上只有有效字符是可选的（取决于还有哪些候选终点站），其余的字母会被字符 * 取代。

告诉你 \(N\) 处目的地的名称，以及乘客已经输入的若干字符，请你输出键盘目前的状态。

输入格式

• 第一行为一个整数 \(N\)。
• 接下来 \(N\)行，每行一个由大写英文字母组成的长度不超过 \(100\) 的字符串，表示一处目的地。
• 最后一行，一个长度不超过 \(100\) 的字符串，表示按顺序输入的若干字符。

输出格式

• 输出 \(4\) 行，每行一个长度为 \(8\) 的字符串，表示键盘状态。

样例数据

样例输入&1

4
ZAGREB
SISAK
ZADAR
ZABOK
ZA

样例输出&1

****B*D*
*G******
********
********

样例解释&1

输入 ZA 以后，下一个字符可能是 G（终点站有可能是 ZAGREB），或 D（终点站有可能是 ZADAR），或 B（终点站有可能是 ZABOK）。

数据范围与约束

• \(N(1≤N≤50)\)

包包的精品店

问题描述

包包在商业街新开了一家精品店，专门出售手工制作的限量版包包。开业第一天，就有 \(n\) 位时尚达人慕名而来。每位顾客都对包包的独特设计赞不绝口，但他们愿意支付的最高价格却不尽相同。

作为精明的店主，包包需要为这款限量包包定一个最合适的价格，既要让尽可能多的顾客能够购买，又要让店铺的总收入最大化。这真是个令人头疼的问题！

每位顾客 \(i\) 都有一个心理价位 \(a_i\) ——这是他们愿意为这个包包支付的最高价格。如果包包最终的定价不超过 \(a_i\)，这位顾客就会开心地买下包包；否则，他们只能遗憾地离开。

包包需要从所有顾客的心理价位中选择一个定价 \(p\) ,你的任务是帮助包包找出能获得最大总收入，总收入是指购买商品的人数乘以商品的价格。

输入格式

• 第一行：单个整数 \(n\)
• 第二行：\(n\) 个整数 \(a_1,a_2,…,a_n\)

输出格式

• 输出一个整数表示最大总收入

样例数据

样例输入&1

5
50 100 110 120 60

样例输出&1

300

样例解释&1

设定商品价格为\(100\)元是最好的选择

数据范围与约束

• 对于\(30\%\)的数据，\(1≤n≤10^3\)
• 对于\(60\%\)的数据，\(1≤n≤5 \times 10^3\)
• 对于\(100\%\) 的数据，\(1≤n≤2\times 10^5\)，\(1≤a_i≤10^6\)

包包的数字游戏

问题描述

包包有一个神奇的数字 \(s\)，它只能是 \(0\) 或 $1 $。包包决定对这个数字进行 \(n\) 轮扩张游戏，最终形成一个 \(2^n \times 2^n\) 的魔法矩阵。每轮扩张的规则如下：

• 当遇到数字 \(0\) 时，会将其变成矩阵：
  \( \begin{pmatrix} 0 & 0 \\ 0 & 1 \\ \end{pmatrix} \)

• 当遇到数字 \(1\) 时，会将其变成矩阵：
  \( \begin{pmatrix} 1 & 1 \\ 1 & 0 \\ \end{pmatrix} \)

包包需要你的帮助来完成这个魔法矩阵的构建！

输入格式

• 第一行：两个整数 \(n\) 与 \(s\)，分别表示扩张轮数和初始数字

输出格式

• 输出\(2^n \times 2^n\)的矩阵，矩阵元素之间不含空格

样例数据

样例输入&1

2 0

样例输出&1

0000
0101
0011
0110

样例解释&1

包包从数字 \(0\) 开始，经过 \(2\)轮扩张：

1. 第一轮扩张：

   • \(0\) 变成：
     \( \begin{pmatrix} 0 & 0 \\ 0 & 1 \\ \end{pmatrix} \)

   • 得到矩阵：

     00
     01
     

2. 第二轮扩张：

   • 每个元素分别扩张：

     • \(0\) 变成：
       \( \begin{pmatrix} 0 & 0 \\ 0 & 1 \\ \end{pmatrix} \)
     • \(1\) 变成：
       \( \begin{pmatrix} 1 & 1 \\ 1 & 0 \\ \end{pmatrix} \)

   • 组合后得到最终矩阵：

     0000
     0101
     0011
     0110
     

数据范围与约束

• \(s=0\) 或 \(1\)
• \(0≤n≤11\)

包包的包子技巧

问题描述

包包是一位包子大师，他可以学习 \(N\) 种包子制作技巧，这些技巧分别标号为 \(1, 2, ……, N\)。要学习每个技巧 \(i\)，他需要花费 \(T_i\) 时间进行练习，并且在开始时必须已掌握技巧 \(A_{i,1}, A_{i,2}, ……, A_{i,K_i}\)。这里保证了，每个前置技巧的编号小于当前技巧编号，即 \(A_{i,j}<i\)。

在时刻 \(0\)，包包还没有掌握任何技巧。他一次只能进行一个技巧的练习，并且一旦开始练习，便不能中途停下。你的任务是计算出包包学习到技巧 \(N\) 所需的最短时间。

输入格式

• 第一行输入一个正整数 \(N\) 表示有 \(N\)个技巧
• 接下来一共有 \(N\) 行，每行先有两个数 \(T\)、\(K\)，表示该技巧需要花费 \(T\)时间学习，而且需要有 \(K\) 个前置技巧。接着有 \(K\)个数，分别表示当前技巧所需的前置技巧。

输出格式

• 输出包包掌握技巧 \(N\) 所需的最短时间。

样例数据

样例输入&1

3
3 0
5 1 1
7 1 1

样例输出&1

10

样例解释&1

包包可以采取这样的学习顺序：

• 他在时刻 \(0\) 开始学习技巧 \(1\)，到时刻 \(3\) 时掌握此技巧。
• 然后，从时刻 \(3\) 开始练习技巧 \(3\)，到时刻 \(10\) 时学会此技巧。 这样一来，包包学习到技巧 \(3\) 的最短时间为 \(3+7=10\)。在这过程中，他不需要掌握技巧 \(2\)。

样例输入&2

5
1000000000 0
1000000000 0
1000000000 0
1000000000 0
1000000000 4 1 2 3 4

样例输出&2

5000000000

数据范围与约束

• $1 \leq N \leq 2 \times 10^5 $
• \(1 \leq T_i \leq 10^9\)
• \(0≤K_i<i\)
• \(1≤A_{i,j}<i\)
• \(\sum\limits_{i=1}^N K_i \leq 2 \times 10^5\)
• \(A_{i,1}, A_{i,2}, ……, A_{i,K_i}\) 全部互不相同。
• 所有输入均为整数。

包包的包子展览

问题描述

包包正在准备一场重要的包子展览。展览需要摆放 \(N\) 个包子，这些包子有不同的馅料编号。为了让展览更美观，包包希望这些包子能摆成回文形状——即从前往后和从后往前看馅料顺序都一样。

包包可以进行以下操作：

• 选择两种馅料编号 \((x,y)\)，把展览中所有 \(x\) 号馅料的包子都换成\(y\) 号馅料

请问包包最少需要进行多少次操作，才能让包子摆成完美的回文形状？

输入格式

• 第一行输入一个数 \(N\) ，表示一共有 \(N\) 种馅料
• 接下来有 \(N\) 个数，表示每种馅料的种类

输出格式

• 输出包包需要的最少操作次数。

样例数据

样例输入&1

8
1 5 3 2 5 2 3 1

样例输出&1

2

样例解释&1

初始包子馅料：1(豆沙)5(奶黄) 3(莲蓉) 2(芝麻) 5(奶黄) 2(芝麻) 3(莲蓉) 1(豆沙)

1. 把3(莲蓉)包子都换成2(芝麻)馅
2. 把2(芝麻)包子都换成5(奶黄)馅 最终变成：1 5 5 5 5 5 5 1，完美对称！

样例输入&2

7
1 2 3 4 1 2 3

样例输出&2

1

样例输入&3

1
200000

样例输出&3

0

数据范围与约束

• \(1≤N≤2×10^5\)
• 包子馅料编号\(1≤A_i≤2×10^5\)