模拟赛SXJ202507270900题目

亮度调节

问题描述

某智能家居系统中有一个节能灯泡，当前亮度为 $n\%$。每分钟，用户可以选择以下两种操作之一：

调亮模式：亮度增加 $2\%$；
调暗模式：亮度减少 $3\%$。

用户希望找到最少需要多少分钟，才能将灯泡亮度调整为恰好 $50\%$。

注意：亮度必须始终保持在 $0\%$ 到 $100% $之间（包含 $0\%$ 和 $100\%$）。具体规则如下：

当亮度 低于 $3\%$时，系统强制开启调亮模式（避免完全熄灭）；
当亮度 高于 $98\%$ 时，系统禁止调亮模式（避免过亮损坏灯泡）。

输入格式

第一行一个整数 $T$，表示测试数据组数；
接下来每组数据一行，包含一个整数 $n$，表示灯泡的初始亮度。

输出格式

每组数据输出一行，表示达到 $50\%$ 亮度的最少分钟数。

样例数据

样例输入&1

样例输出&1

样例解释&1

对于第一组数据，先调亮 $1$ 下，再调暗 $1$ 下。

对于第三组数据，先调亮 $15$ 下，再调暗 $1$ 下。

数据范围与约束

对于 $30\%$ 的数据，$T=1$，$49≤n≤51$。
对于 $60\%$ 的数据，$T≤10$，$40≤n≤60$。
对于 $100\%$的数据，$1≤T≤1000$，$0≤n≤100$。

音乐播放

问题描述

你有一个音乐播放器，里面有 $N$ 首歌曲（编号从 $1$ 到$ N$）。每首歌曲有一个初始的"权重值" $R_i$。播放器按照以下规则选择播放的歌曲：
1. 选择歌曲：每次播放当前权重值最大的歌曲。如果有多首歌曲权重相同，选择编号最小的那首。
2. 权重分配
  
  ：播放完一首歌曲后：
  - 该歌曲的权重值会被平均分配给其他所有歌曲（N-1首）
  - 如果不能整除，余数部分会按顺序一个一个分配给前面的歌曲（跳过刚播放的那首）
  - 播放完的歌曲权重值归零
3. 重复这个过程，直到播放了 T 首歌曲。
你需要输出前 T 首被播放的歌曲编号。

输入格式

第一行：两个整数 $N$ 和 $T$
接下来 $N$ 行：每行一个整数，表示每首歌曲的初始权重值

输出格式

$T$ 行：每行一个整数，表示第 $i$ 首播放的歌曲编号

样例数据

样例输入&1

样例输出&1

样例解释&1

样例1：初始权重：$[10, 8, 11]$

第一首：播放 $3$（权重$11$最大）
- 分配：$11 ÷ 2 = 5 余1$
- 余数$1$给$1$（跳过$3$）
- 新权重：$[10+5+1=16, 8+5=13, 0]$
第二首：播放 $1$（权重$16$最大）
- 分配：$16 ÷ 2 = 8 余0$
- 新权重：$[0, 13+8=21, 0+8=8]$
第三首：播放 $2$（权重$21$最大）
- 分配：$21 ÷ 2 = 10 余1$
- 余数$1$给$1$（跳过$2$）
- 新权重：$[0+10+1=11, 0, 8+10=18]$
第四首：播放 $3$（权重$18$最大）
- 结束

样例输入&2

样例输出&2

1
5

样例解释&2

样例2： 初始权重：$[18,3,8,11,13]$

第一首：播放 $1$（权重$18$最大）

分配：$18 ÷ 4 = 4 余 2$
余数$2$分别给$2$ $3$（跳过$1$）
新权重：$[0,3+4+1=8,8+4+1=13,11+4=15,13+4=17]$

第二首：播放 $5$（权重$17$最大）

数据范围与约束

$1≤N≤1,000$
$1≤R_i≤10,000$
$1≤T≤1000$

任务调度

问题描述

某工厂有 $N$ 个生产任务，编号为 $1$ 到$ N$。这些任务需要按照特定顺序在流水线上完成。任务调度受到两种约束条件限制：
1. 依赖链约束：$M$ 个任务存在依赖关系，必须按照给定顺序完成。例如，若输入链为 $[4,5,6]$，则任务 44 必须在任务 $5$ 前完成，任务 $5$ 必须在任务 $6$ 前完成。
2. 固定位置约束：$K$ 个任务必须在流水线的特定位置完成。例如，输入"5 3"表示任务 $5$ 必须在第 $3$个位置完成。
任务 $1$ 是紧急任务，工厂主管希望尽早完成它。请确定在满足所有约束条件下，任务 $1$ 可以完成的最早位置。

输入格式

第一行：$N$（任务总数），$M$（依赖链中的任务数），$K$（有固定位置的任务数）
第二行：$M$ 个不同的任务 $ID$，表示依赖链中的任务顺序
随后 $K$ 行：每行一个任务 $ID$ ，$c_i$和位置 $p_i$，表示任务 $c_i$ 必须在第 $p_i$ 位完成

输出格式

输出任务 $1$ 可以完成的最早位置

样例数据

样例输入&1

样例输出&1

样例解释&1

工厂有 $6 $个任务：

依赖链：$任务 4 → 任务 5 → 任务 6$
固定位置：$任务 3 $必须在第 $1$ 位，$任务 5$ 必须在第 $3$ 位

可行的调度顺序：

$任务 3$（固定位置 $1$）
$任务 4$（必须在任务$ 5 $之前）
$任务 5$（固定位置 $3$）
$任务 1$（最早可能位置）
$任务 6$（必须在任务 $5$ 之后）
剩余任务

因此任务 $1$ 的最早完成位置是第$ 4$ 位。

数据范围与约束

$2≤N≤100$
$1≤M,K<N$
$1≤c_i,p_i<N$

包包的魔法世界

问题描述

包包在玩一个有趣的游戏世界，这里有$N$个魔法节点，编号从 $1$ 到 $N$。这些节点通过魔法能量连接成一棵以节点 $1$ 为源头的魔法树。第 $i$ 条魔法连接$（1≤i≤N−1）$将节点 $a_i$ 和 $b_i$ 相连。

每个魔法节点都有一个能量计数器，初始时所有计数器的值都为 $0$。

现在包包要进行 $Q$ 次魔法充能：

第 $j$ 次充能$（1≤j≤Q）$：选择以节点 $p_j$为源头的魔法子树，将该子树中所有节点的能量计数器增加 $x_j$ 点魔法值。

包包想知道，在所有充能操作完成后，每个魔法节点的能量计数器最终数值是多少？

输入格式

第一行输入两个数 $N$ 、 $Q$ 表示魔法节点数和操作次数。
接下来有 $N−1$ 行，每行两个数 $u$ 、 $v$，表示该两个节点相连接；
接下来有 $Q$ 行，每行两个数， $p$、 $x$ ，表示给以 $p$为根节点的子树上每一个节点都加上 $x$ 。

输出格式

请输出节点 $1$ 到$N$ 的最终能量值，用空格分隔。

样例数据

样例输入&1

样例输出&1

100 110 111 110

样例解释&1

魔法树结构如下：

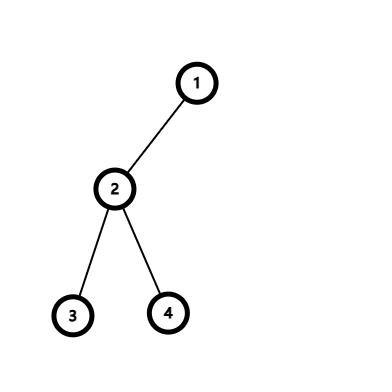
充能过程：

对以$②$为源的子树$②③④$充能$+10$
- 计数器：$0,10,10,10$
对以$①$为源的整棵树$①②③④$ 充能$+100$
- 计数器：$100,110,110,110$
对以$③$ 为源的子树（仅$③$）充能$+1$
- 最终计数器：$100,110,111,110$

样例输入&2

样例输出&2

20 20 20 20 20 20

数据范围与约束

魔法节点数：$2≤N≤2×10^5$
充能次数：$1≤Q≤2×10^5$
魔法连接：$1≤a_i<b_i≤N$
充能目标：$1≤p_j≤N$
充能数值：$1≤x_j≤10^4$
保证构成一棵有效的魔法树
所有输入均为整数

奇怪的银行

问题描述

某银行为了增加取款难度，规定客户每次操作只能取出以下金额之一：

$1$ 元
$6$ 的幂次金额：$6 元$（$6^1$）、$36$ 元（$6^2$）、$216$ 元（$6^3$）...
$9$ 的幂次金额：$9$ 元（$9^1$）、$81$ 元（$9^2$）、$729$ 元（$9^3$）...

问：要恰好取出总共 $N$ 元，至少需要进行多少次取款操作？不允许将已取出的钱重新存入。

输入格式

输入一个整数$ N$。

输出格式

输出一个整数表示最少需要的操作次数。

样例数据

样例输入&1

样例输出&1

样例解释&1

最优方案：

取出 $1$ 元（操作 $1$）
取出 $9$ 元（$9^1$，操作 $2$）
取出 $36$ 元（$6^2$，操作 $3$）
取出 $81$ 元（$9^2$，操作 $4$）总和：$1 + 9 + 36 + 81 = 127 元$

样例输入&2

样例输出&2

样例输入&3

样例输出&3

数据范围与约束

$1≤N≤10^5$
$N$为整数

posted @ 2025-07-27 15:13 Kevinrzy103874 阅读(15) 评论(0) 收藏举报

刷新页面返回顶部

KevinSystemOlineJudge

Kevinrzy103874

模拟赛SXJ202507270900题目

亮度调节

问题描述

输入格式

输出格式

样例数据

样例输入&1

样例输出&1

样例解释&1

数据范围与约束

音乐播放

问题描述

输入格式

输出格式

样例数据

样例输入&1

样例输出&1

样例解释&1

样例输入&2

样例输出&2

样例解释&2

数据范围与约束

任务调度

问题描述

输入格式

输出格式

样例数据

样例输入&1

样例输出&1

样例解释&1

数据范围与约束

包包的魔法世界

问题描述

输入格式

输出格式

样例数据

样例输入&1

样例输出&1

样例解释&1

样例输入&2

样例输出&2

数据范围与约束

奇怪的银行

问题描述

输入格式

输出格式

样例数据

样例输入&1

样例输出&1

样例解释&1

样例输入&2

样例输出&2

样例输入&3

样例输出&3

数据范围与约束

公告