模拟赛SXJ202507250900题目

速冻饺子

题目描述

包包在 $n$天时间里，每天都要吃一盘水饺。

水饺每天的价格都不一样。在第 $i$ 天，水饺的价格为每份$a_i$ 元。

可以未雨绸缪，提前多买几份水饺放在冰箱里冷冻。但每份水饺每保存一天需要支付存储费$c$ 元。

假设每天可以买无限多的水饺，冰箱的容量也是无限的，请问应该如何购买水饺才能使支付的总费用达到最小？

输入格式

第一行：两个整数：表示$n$与 $c$
第二行：$n$ 个整数：表示 $a_1$ 到$a_n$

输出格式

单个整数：表示答案。

输入输出样例

样例输入&1

5 3
10 20 20 20 20

样例输出&1

样例解释&1

$10+13+16+19+20=78$

数据规模与约定

$30\%$ 的数据，$1≤n≤20$
$60\%$的数据，$1≤n≤1,000$
$100\%$的数据，$1≤n≤100,000$
$1≤c,a_i≤20,0001≤c,a_i≤20,000$

披萨

题目描述

我们有一个圆形的比萨饼。

包包将使用长度为$n$的序列$a$切割这个披萨，按照以下步骤。

首先，从中心沿$12:00$方向切一刀。
下一步，执行$n$操作。第$i$ 次操作如下:
- 顺时针旋转披萨$a_i$ 度。
- 然后，从中心沿 $12:00$方向切割。

例如，如果 $a=(90,180,45,195)$ ，该过程将按如下方式切割披萨。

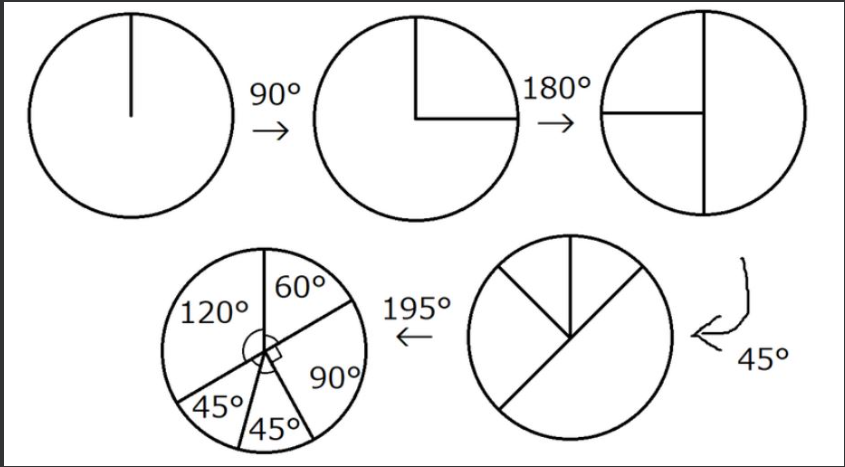
算出最大的披萨的圆心角。

输入格式

第一行：单个整数$n$ ；
第二行：输入$n$个整数$a_i$

输出格式

输出最大的披萨的圆心角。

输入输出样例

样例输入&1

4
90 180 45 195

样例输出&1

样例输入&2

10
215 137 320 339 341 41 44 18 241 149

样例输出&2

数据规模与约定

$1≤n≤359$
$1≤a_i≤359$
$不会在同一位置有多次切割$

包包的美术课

题目描述

今天包包的美术老师带来了一张画布，画布上已经有了当下的风景。

我们设画布的长度是$n$，每一单位长度上的颜色可以用一个在$[1,k]$范围内的正整数表示。

包包需要在上面重新作画。每一次作画，他可以选定画布上的任意一个位置，然后将这个位置上的颜色涂改成$[1,k]$范围内的任意正整数。

我们定义为画上的相同颜色连续块个数为记忆碎片。现在包包想知道，如果给定他作画的次数上限，那么画上的记忆碎片个数最多有多少。

输入格式

本题有多组测试数据
第一行输入一个正整数$t$表示数据组数。
对于每组测试数据，第一行输入三个正整数 $n$,$m$,$k$,表示画布的长度，包包作画的次数上限和颜色的取值范围。
第二行输入一个长度为$n$的整数序列 $c$，表示画布上每个位置的初始颜色。

输出格式

对于每组测试数据，输出一行一个正整数，表示记忆碎片最多有多少个。

输入输出样例

样例输入&1

样例输出&1

样例解释&1

对于第一组测试数据，包包可以将从左到右的第二个位置涂成颜色$1$，得到 $\{c_n\} = \{2, 1, 2\}$，块数为 $3$。

对于第二组测试数据，包包可以将从左到右的第二个位置涂成颜色 $1$，将从左到右的第三个位置涂成颜色$3$，得到 $\{c_n\} = \{2, 1, 3, 2, 3\}$数为 $5$。

数据规模与约定

$40\%$ 的数据，$ 1≤t≤10，1≤∑n≤1000，1≤m≤n，3≤k≤100，1≤c_i≤k$
$100\%$的数据，$ 1≤t≤5 \times 10^3，1≤∑n≤5 \times 10^5，1≤m≤n，3≤k≤5 \times 10^5，1≤c_i≤k$

包包的探店之旅

题目描述

包包为了更新包子店的菜单，会时常去别的餐厅探店进行学习。

这次包包探店的是一家以危险著称的餐厅，通过尝试食用危险食品后及时服用解药做成的菜品而出名。

包包在这家餐厅享用由$n$道菜组成的有线全套餐。第 $i$ 道菜是：

如果 $X_i=0$，这是一道解毒菜，美味度为 $Y_i$；
如果 $X_i=1$，这是一道有毒菜，美味度为 $Y_i$。

当包包吃一道菜时，他的状态会按以下方式变化：

初始时，包包有一个健康的胃。
当他的胃健康时：
- 如果他吃解毒菜，胃保持健康；
- 如果他吃有毒菜，他会胃部不适。
当他胃部不适时：
- 如果他吃解毒菜，胃恢复健康；
- 如果他吃有毒菜，他会死亡。

用餐过程如下：

对于 $i=1,…,N$，按顺序重复以下过程：

首先，第 $i$ 道菜被端给包包。
接着，他选择“吃”或“跳过”这道菜。
- 如果他选择“吃”，他会吃第$i$道菜，并根据所吃的菜改变状态。
- 如果他选择“跳过”，他不会吃这道菜，且这道菜之后不能再吃或保存。
最后（如果状态改变，则在改变后），如果他未死亡：
- 如果 $i \neq N$，他继续下一道菜；
- 如果 $i=N$，他成功活着离开餐厅。

包包只是过来学习的，因此他必须活着离开餐厅。但是他又希望尽可能吃到更大的美味值以学习更多东西。

所以在满足该条件的情况下，找出他所吃菜肴的最大可能美味度总和（如果他什么也没吃，则为 0 ）。

输入格式

第一行输入一个数$n$ ，表示套餐内有$n$道菜。
接下来$n$行，每行两个数$X_i$ 和 $Y_i$ ，分别表示这道菜的类型为且其$X_i$美味值为 $Y_i$。

输出格式

输出一个整数，表示包包或者离开餐厅时所能得到的最大美味值。

输入输出样例

样例输入&1

样例输出&1

样例解释&1

以下选择方式使得他所吃菜肴的总美味度达到最大值 $600$：

他跳过第 $1$ 道菜，胃保持健康。
他吃第 $2$ 道菜，胃部不适，总美味度为 $300$。
他吃第 $3$ 道菜，胃恢复健康，总美味度为 $100$。
他吃第 $4$ 道菜，胃部不适，总美味度为 $600$。
他跳过第 $5$ 道菜，胃部不适。最终，他未死亡，成功活着离开餐厅。

样例输入&2

样例输出&2

样例解释&2

最优选择是什么也不吃，此时答案为$0$。

样例输入&3

15
1 900000000
0 600000000
1 -300000000
0 -700000000
1 200000000
1 300000000
0 -600000000
1 -900000000
1 600000000
1 -100000000
1 -400000000
0 900000000
0 200000000
1 -500000000
1 900000000

样例输出&3

4100000000

数据规模与约定

所有输入值均为整数。
$1≤N≤3×10^5$
$X_i \in \{0, 1\}$（即 $X_i$ 为 $0$ 或 $1$）。
$−10^9≤Y_i≤10^9$

包包的炼金厨房

题目描述

包包的厨房里有$n$种食材，编号从 $1$ 到$n$ 。包包再之前的学习中学会了 $m$ 道加工工序，编号从 $1$ 到 $m$。通过工序 $i$，可以在 $1$ 小时内将食材 $A_i$和食材 $B_i$ 互相转化（比如把鸡肉变成鸡汤，或者把鸡汤还原成鸡肉）。

虽然小强老是吐槽包包学回来的是炼金术（毕竟是相互转化，谁做出来的鸡汤能变回鸡肉的）。但是现在小强想要得到食材 $n$，所以只好拜托包包帮忙处理。

包包想知道：从初始食材 $1$ 到目标食材$n$的最快转化方案有多少种？由于答案可能很大，请对 $10^9+7$取模。

如果无法从食材$1$ 得到食材$n$ ，则输出 0 。

输入格式

第一行输入两个数$n$ 、$m$，分别表示有$n$个食材和包包学会的$m$道加工工序。
接下来$m$行，每行输入两个数，表示可以相互转化的两种食材。

输出格式

输出从食材 $1$ 到食材$n$的最快转化的方案总数，对 $10^9+7$取模。
若不可转化，则输出 0 。

输入输出样例

样例输入&1

样例输出&1

样例解释&1

最快需要 $2$ 小时，有两条转化路径：

$食材1 → 食材2 → 食材4$
$食材1 → 食材3 → 食材4$

样例输入&2

样例输出&2

样例解释&2

最快需要$3$ 小时，唯一路径：

$食材1 → 食材3 → 食材2 → 食材4$

样例输入&3

2 0

样例输出&3

样例解释&3

食材$1$无法转化为食材$2$

样例输入&4

样例输出&4

数据规模与约定

$2≤n≤2×10^5$
$0≤m≤2×10^5$
$1≤A_i<B_i≤n$
所有工序的 ($A_i$,$B_i$)组合都是唯一的

posted @ 2025-07-25 15:00 Kevinrzy103874 阅读(20) 评论(0) 收藏举报

刷新页面返回顶部

KevinSystemOlineJudge

Kevinrzy103874

模拟赛SXJ202507250900题目

速冻饺子

题目描述

输入格式

输出格式

输入输出样例

样例输入&1

样例输出&1

样例解释&1

数据规模与约定

披萨

题目描述

输入格式

输出格式

输入输出样例

样例输入&1

样例输出&1

样例输入&2

样例输出&2

数据规模与约定

包包的美术课

题目描述

输入格式

输出格式

输入输出样例

样例输入&1

样例输出&1

样例解释&1

数据规模与约定

包包的探店之旅

题目描述

输入格式

输出格式

输入输出样例

样例输入&1

样例输出&1

样例解释&1

样例输入&2

样例输出&2

样例解释&2

样例输入&3

样例输出&3

数据规模与约定

包包的炼金厨房

题目描述

输入格式

输出格式

输入输出样例

样例输入&1

样例输出&1

样例解释&1

样例输入&2

样例输出&2

样例解释&2

样例输入&3

样例输出&3

样例解释&3

样例输入&4

样例输出&4

数据规模与约定

公告