7.24模拟

Editorial

A. 光

12/44pts

暴力分。

性质 1 12pts

性质：原图是一棵树，换根 $dp$ 即可。

80pts

结论 $1$：若结点 $i$ 不在原图的一个最大匹配 $S$ 中，则从 $i$ 开始时先手必败。

证明：考虑与 $i$ 相邻的点 $j$，$j$ 必然在 $S$ 中，否则 $(i,j)$ 不在最大匹配 $S$ 中，与 $S$ 的极大性矛盾。则若先手选择 $j$，后手必然可以选择 $S$ 中与 $j$ 匹配的结点，这样迭代下去，后手总有可以移动的方案。

所以容易得出：若原图去掉 $i$ 后最大匹配的大小不变，后手必胜，否则先手必胜。

算法 $1$：每次删点之后用最大流求最大匹配。复杂度：$O(n^\frac{3}{2}m)$。通过极致的卡常可以拿到 $80$ 分。

算法 $2$：

先用匈牙利算法求出原图的最大匹配，对于每个结点 $i$，若其不在匹配中，后手必胜，否则考虑与 $i$ 匹配的 $j$，在删去 $i$ 之后能不能通过其他结点增广。

判断能否增广：先考虑二分图左侧（染成黑色的点），对于边 $(i,j)$，若没有在匹配中，从左侧连到右侧，否则从右侧连到左侧。若从一个未在匹配中的左侧点可以走到点 $i$ 则点 $i$ 可以被增广掉（也就是说 $i$ 不是必须的），右侧点同理。

复杂度 $O(nm)$。

100pts

考虑优化 $80$ 分的做法，使用 Dinic 跑最大匹配，之后找最大流的增广路即可。

复杂度 $O(m\sqrt n)$。

匹配

匹配是啥？匹配就是一些边的集合，使得它们的端点互不相同，也就是说，没有一个点被包含在至少两条边中。

最大匹配就是边数最多的匹配。

如何求二分图的一个最大匹配？可以使用匈牙利算法。

例如图：

$l_1$ $r_1$

$l_2$ $r_2$

$l_3$ $r_3$​

$l_4$ $r_4$

$l_1 - r_1,r_2,r_3$

$l_2 - r_1,r_2$

$l_3-r_1$

$l_4 - r_1$

首先给 $l_1$ 找一个匹配，不妨就设 $l_1-r_1$。

下面给 $l_2$ 找一个匹配，因为 $r_1$ 匹配过了，就让 $l_2-r_2$。

然后给 $l_3$ 找匹配，发现 $r_1$ 已经跟 $l_1$ 匹配过了，$l_3$ 没法匹配了，但是发现 $l_1$ 可以改成跟 $r_3$ 匹配，于是 $l_1-r_3,l_3-r_1$。

最后 $l_4$ 也想跟 $r_1$ 匹配，但是跟 $r_1$ 匹配的 $l_3$ 没有办法修改了，于是 $l_4$ 无法匹配。

模拟这个过程即可，复杂度 $O(nm)$。

也可以使用最大流算法，它的复杂度是 $O(m\sqrt n)$。

最大流

最大流又是啥？

网络是一个有向的带权图，每条边的权值（正数）称作容量，网络还需要有源点 $s$ 和汇点 $t$。

我们想最大化网络的流量，但是又不能超过每条边的流量。形式化地：

1. 每条边的流量 $f_e$ 满足 $0\leq f_e\leq c_e$，其中 $c_e$ 是容量。
2. 对于除源点汇点外的一个节点 $u$，流入 $u$ 的流量和应等于流出 $u$ 的流量和。

一个流的流量是流出 $s$ 的所有边的流量和，我们想通过给每条边安排一个流量来最大化它。

Edmonds-Karp

怎样求最大流？

我们可以从 $f_e=0$ 的空网络开始，每次在流网络中找到一条从 $s$ 到 $t$ 的路径，并且路径上的每条边都没有满流（$f_e<c_e$），并每次给这个路径上的所有边流量 $+1$。我们发现同一条路径其实可以 $+1$（或称为增广）多次，所以我们一次增广就直接 $+1$ 至至少有一条边满流为止（即 $+\min\{c_e-f_e\}$）。

但是这种做法实际上是错误的。

例如：

 

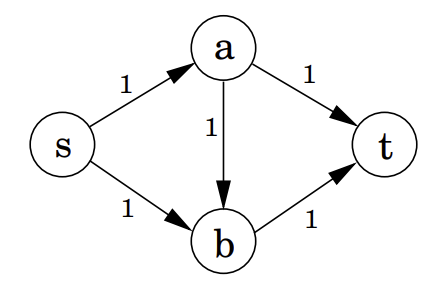
这个网络的最大流显然是 $2$，但是如果第一次增广了 $s\rightarrow a\rightarrow b\rightarrow t$ 后就无法再增广，得到的结果是 $1$。

所以我们需要把走错的流推回去，增广路径上不仅要包括原图没有满流的边，还要包括原图中有流的边的反边。

形式化的，每次增广要在图上找到一条 $s$ 到 $t$ 的路径。图由两种边组成：

1. 原图中的边 $(u,v)$ 且它没有满流。
2. $(v,u)$ 使得原图中有边 $(u,v)$ 且 $(u,v)$ 的流不为 $0$。

我们只需要在这个图上找到增广路径即可，可以使用 bfs+dfs 模拟这个过程。

复杂度：$O(nm^2)$。

二分图最大匹配

对于二分图左侧的点 $u$，从 $s$ 向 $u$ 连边权为 $1$ 的边。

对于二分图右侧的点 $v$，从 $v$ 向 $t$ 连边权为 $1$ 的边。

对于图上的边 $(u,v)$，设 $u$ 在左侧，$v$ 在右侧，从 $u$ 向 $v$ 连边权为 $1$ 的边。

最大流的流量就是这个图的最大匹配数。

证明可由最大流的性质（若容量均为整数则最大流上每个边的流量均为整数）来证明，留做习题。

B. 对立

10pts

全排列。

性质 2 30pts

把每个字符串 $s=s_0s_1$ 看做一条边 $(s_0\rightarrow s_1)$，要求的就是一条欧拉回路，dfs 后倒序输出即可。

性质 3 20pts

随机且 $m\geq 200$ 使对于子串 $s$，满足能放在它之后的子串个数（即 $s$ 的后 $m-1$ 个字符和这个串的前 $m-1$ 个字符相等）很少，暴搜即可。

100pts

将每个子串 $s=s_1\dots s_m$ 看做从 $s[1,m-1]$ 到 $s[2,m]$ 的一条边，先对字符串离散化再跑欧拉回路输出即可。

复杂度 $O(nm \log m)$。

Euler Trail

如何求一个欧拉路？用 Fleury 算法即可。伪代码：

DFS(u):
　　While(find an edge (u,v))
　　　　delete edge e(u,v)
　　　　DFS(v)
　　End
　　PathSize←PathSize+1
　　Path[PathSize]←u

最后 Path 需要倒序输出。而算法的初始结点（欧拉路的第一个结点）就是唯一一个入度小于出度的点，若没有这样的点则任选一个即可。

C. 红

40pts

暴力。

100pts

观察到 hollow 和 colorful 是等价的，desolate 和 scarlet 是等价的。

于是简化为种类的奇偶性不同才可以匹配。

贪心的想，子树内能匹配的一定尽量匹配，如果能匹配的不在子树内匹配，则连向父亲的边会不必要的算在代价内。

对于每个结点 $f(x)$ 记录一下剩余几个核心，正代表奇数，负代表偶数，则 $f(i)=x_i+\sum\limits_{j\in son(i)} f(j)$，而每个结点向父亲的连边的贡献（即经过该边的配对数）就是子树内剩余的核心数量，即 $|f(x)|$。

一遍 dfs 求出答案。

复杂度 $O(n)$。

D. 咲弥

25pts

暴力分。

50pts

观察到一定是前一段人使用机器后一段人使用记忆训练，枚举分段点，对于分段点 $p$ 的答案为 $\max\{t[p]+y,\max\limits_{i=1}^{p-1}(t[i]+xi)\}$，二分满足它最优的 $y$ 的区间即可。

复杂度 $O(n \log m+m)$。

性质 1 20pts

观察到若 $y\leq x$，不需要使用机器，答案就是 $d_1+y$。只需对 $y>x$ 的情况处理即可。

复杂度 $O(m+(m-x)n)$。

100pts

考虑优化 $50$ 分的算法，观察到对于 $y$ 越来越大，分段点的位置是单调不降的，two pointers 维护即可。注意到空间只有 $12\text{MB}$，甚至开不下一个 $10^7$ 长度的数组，但是注意对于分段点 $p$ 的代价，无需存储所有的 $t[i]$，而是在不断读入的过程中记录 $\max\limits_{i=1}^{p-1}(t[i]+xi)$ 即可。

时间复杂度 $O(n+m)$，空间复杂度 $O(1)$。