2025 ICPC 西安区域赛 BFGIJLM
没留代码说明是现场时写的。
B. Beautiful Dangos
二分,贪心。
先找出左右两边第一次遇到的相邻颜色相同的区间 \([l,r]\),那么 \([1,l]\) 和 \([r,n]\) 就是可选的部分,此时可以枚举 \([1,l]\),二分 \([r,n]\),因为 \([l,r]\) 是必须重排的区间,在此基础上加入更多可选颜色时,显然重排不相邻的可能性越大。
检验区间时,先看颜色的数量是否足以满足要求,并要对 \(l-1,r+1\) 的细节讨论一下,放置方案的时候可以先正着动态放一遍最多的,不行再动态放一遍最少的即可。
点击查看代码
#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#include <bits/stdc++.h>
#define int long long
#define PII pair<int,int>
#define PIII pair<PII,int>
using namespace std;
//#define endl '\n'
const int N = 2e6 + 10, mod = 1e9 + 7;
int top;
int n, m, k;
string s;
string str="CWP";
int a[3][N];
void solve() {
cin >> n;
cin>>s;
s='0'+s+'0';
int f=1;
int LL=-1,RR=-1;
for(int i=1;i<=n;i++){
a[0][i]=a[0][i-1];
a[1][i]=a[1][i-1];
a[2][i]=a[2][i-1];
a[0][i]+=s[i]=='C';
a[1][i]+=s[i]=='W';
a[2][i]+=s[i]=='P';
if(i>1){
if(s[i]==s[i-1]){
f=0;
if(LL==-1){
LL=i;
}
RR=i-1;
}
}
}
if(f){
cout<<"Beautiful\n";
return;
}
int mn=n+1,L=-1;
for(int i=1;i<=LL;i++){
int l=max(RR,i+1),r=n;
int ans=-1;
while(l<=r){
int mid=l+r>>1;
int s0=a[0][mid]-a[0][i-1];
int s1=a[1][mid]-a[1][i-1];
int s2=a[2][mid]-a[2][i-1];
int f=1;
if(s0<=s1+s2+1&&s1<=s0+s2+1&&s2<=s0+s1+1){
}else{
f=0;
}
if(s[i-1]=='C'){
s0++;
}else if(s[i-1]=='W'){
s1++;
}else if(s[i-1]=='P'){
s2++;
}
if(s0<=s1+s2+1&&s1<=s0+s2+1&&s2<=s0+s1+1){
}else{
f=0;
}
if(s[mid+1]=='C'){
s0++;
}else if(s[mid+1]=='W'){
s1++;
}else if(s[mid+1]=='P'){
s2++;
}
if(s0<=s1+s2+1&&s1<=s0+s2+1&&s2<=s0+s1+1){
}else{
f=0;
}
if(s[i-1]=='C'){
s0--;
}else if(s[i-1]=='W'){
s1--;
}else if(s[i-1]=='P'){
s2--;
}
if(s0<=s1+s2+1&&s1<=s0+s2+1&&s2<=s0+s1+1){
}else{
f=0;
}
if(f){
ans=mid;
r=mid-1;
}else{
l=mid+1;
}
}
if(ans!=-1){
if(ans-i+1<mn){
mn=ans-i+1;
L=i;
}
}
}
int R=L+mn-1;
if(mn==n+1){
cout<<"Impossible\n";
}else{
cout<<"Possible\n";
cout<<L<<' '<<R<<endl;
char ls='0';
for(int i=1;i<L;i++){
cout<<s[i];
ls=s[i];
}
int s0=a[0][R]-a[0][L-1];
int s1=a[1][R]-a[1][L-1];
int s2=a[2][R]-a[2][L-1];
priority_queue<PII>q;
if(s0)q.push({s0,0});
if(s1)q.push({s1,1});
if(s2)q.push({s2,2});
string ans;
for(int i=L;i<=R;i++){
auto [ss,x]=q.top();
if(str[x]!=ls){
ans+=str[x];
ls=str[x];
q.pop();
if(ss-1){
q.push({ss-1,x});
}
}else{
q.pop();
if(q.size()){
auto [sy,y]=q.top();
ans+=str[y];
ls=str[y];
q.pop();
if(sy-1){
q.push({sy-1,y});
}
}
q.push({ss,x});
}
}
if(ls==s[R+1]){
ls=s[L-1];
while(q.size())q.pop();
ans="";
if(s0)q.push({s0,0});
if(s1)q.push({s1,-1});
if(s2)q.push({s2,-2});
for(int i=L;i<=R;i++){
auto [ss,x]=q.top();
if(str[-x]!=ls){
ans+=str[-x];
ls=str[-x];
q.pop();
if(ss-1){
q.push({ss-1,x});
}
}else{
q.pop();
if(q.size()){
auto [sy,y]=q.top();
ans+=str[-y];
ls=str[-y];
q.pop();
if(sy-1){
q.push({sy-1,y});
}
}
q.push({ss,x});
}
}
}
cout<<ans;
for(int i=R+1;i<=n;i++){
cout<<s[i];
}cout<<endl;
}
}
signed main() {
// freopen("in.txt", "r", stdin);
ios::sync_with_stdio(false);
cin.tie(0);
int t = 1;
cin >> t;
while (t--) {
solve();
}
return 0;
}
F. Follow the Penguins
思维。
按每个人的目标企鹅连边,会发现复杂情况下是一个基环树森林,看起来企鹅们是互相影响的,实则存在一个先后关系,就是对于一个基环树来说,一开始一定是相向而行最短的那个会停下来,然后环就断开了,变成一棵树,此时你可以以停下来的那个点作为根节点然后去更新那些指向它的儿子,也就是说那些儿子的目的地变成了固定的,等它们到达,又去更新它们的儿子...
赛时队友的做法是用 \(set\) 维护相遇的时间,然后枚举到达了几个点,每次到达之后更新指向它的节点即可。
G. Grand Voting
排序。
正反排序算一遍即可。
I. Imagined Holly
解法一:反拓扑建树。
一个比较重要的性质,设 \(d_{x,y}\) 代表 \(x\) 到 \(y\) 的简单路径的异或和,那么有 \(d_{x,y}\oplus d_{x,z}\oplus d_{y,z} = p\),说明在以 \(x\) 为 \(y,z\) 祖先的情况下,可以得出 \(p\) 为 \(y,z\) 的 \(\text{lca}\)。
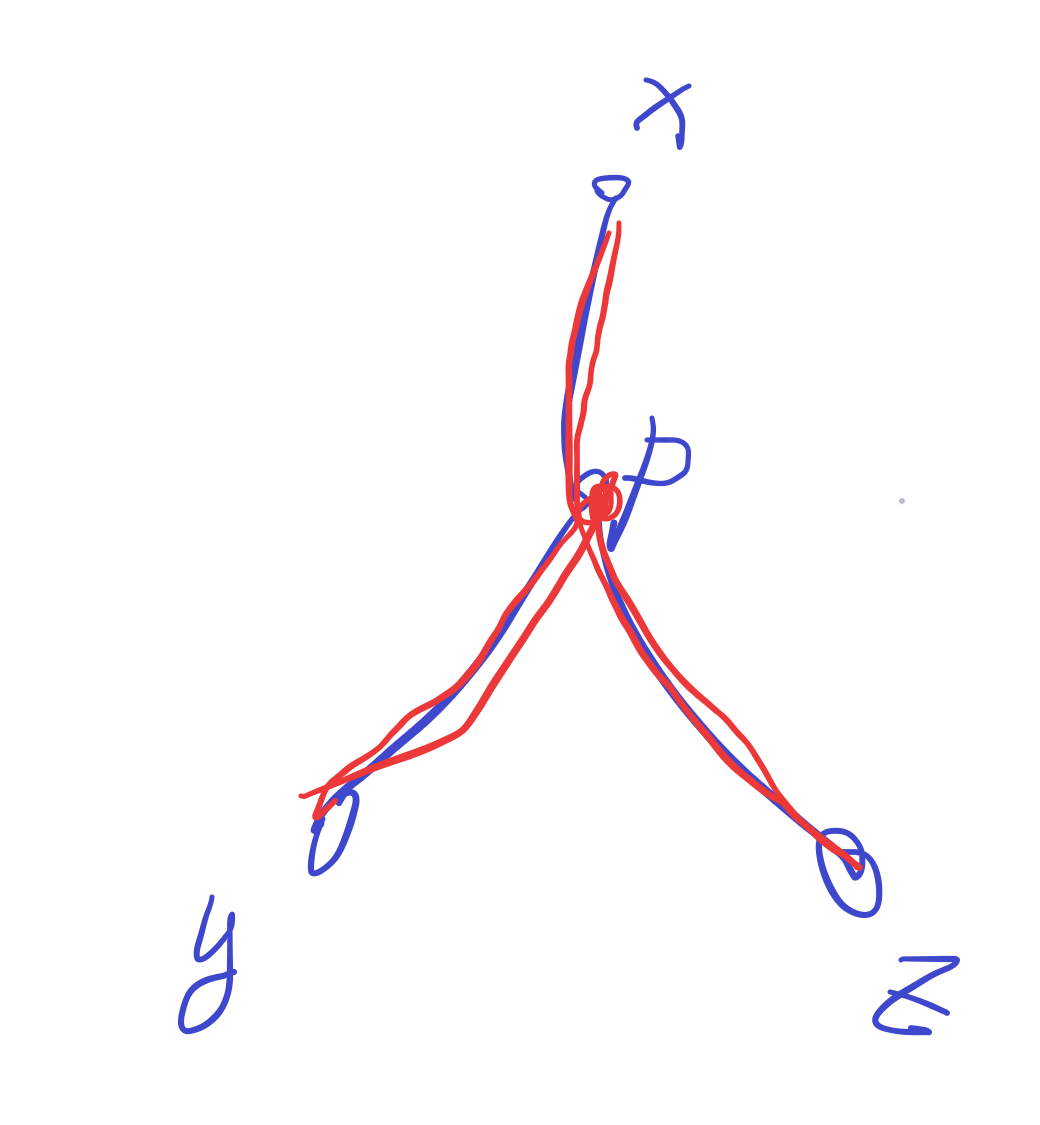
考虑以 \(1\) 为根,那么枚举 \(i,j\),可以用 \(d_{1,i}\oplus d_{1,j} \oplus d_{i,j}\) 得出 \(i,j\) 的相对关系,比如谁相对是谁的祖先节点,然后根据相对关系跑反拓扑排序建树,每次新加点时枚举一遍叶子,判断该点是哪个点的父亲,然后用父亲去覆盖儿子,维护叶子当前更新到哪个点了即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
std::cin >> n;
std::vector a(n + 1, std::vector<int>(n + 1));
for (int i = 1; i <= n; i += 1) {
for (int j = i; j <= n; j += 1) {
std::cin >> a[i][j];
a[j][i] = a[i][j];
}
}
std::vector<int> d(n + 1);
std::vector g(n + 1, std::vector<int>());
std::vector lca(n + 1, std::vector<int>(n + 1));
for (int i = 1; i <= n; i += 1) {
for (int j = i + 1; j <= n; j += 1) {
int x = a[1][i] ^ a[1][j] ^ a[i][j];
lca[i][j] = lca[j][i] = x;
if (x != i) {
g[i].push_back(x);
d[x] += 1;
}
if (x != j) {
g[j].push_back(x);
d[x] += 1;
}
}
}
std::queue<int> q;
std::vector<int> leaf(n + 1);
for (int i = 1; i <= n; i += 1) {
if (!d[i]) {
leaf[i] = i;
q.push(i);
}
}
std::vector has(n + 1, std::vector<char>(n + 1));
while (q.size()) {
auto u = q.front();
q.pop();
for (auto &v : g[u]) {
if (!--d[v]) {
q.push(v);
for (int i = 1; i <= n; i += 1) {
if (leaf[i]) {
int x = leaf[i];
if (a[1][v] == (a[1][x] ^ x) && lca[x][v] == v) {
has[v][x] = 1;
has[x][v] = 1;
leaf[i] = v;
}
}
}
}
}
}
for (int i = 1; i <= n; i += 1) {
for (int j = i + 1; j <= n; j += 1) {
if (has[i][j]) {
std::cout << i << " " << j << "\n";
}
}
}
return 0;
}
解法二:暴力枚举。
对于 \(d_{i,j}=i\oplus j\) 来说,要么直接相连,要么中间有一串 \(0\),假设中间这串 \(0\) 和 \(i\) 相连的点是 \(i\),那么一定有 \(d_{k,j}=j\),能找到这样的点,那么就删掉 \(i-j\) 这条边即可。
能构造出这种非法的边大概有 \(\frac{n^2}{16}\) 条,再加上遇到不合法就 \(\text{break}\),而遇到不合法的概率为 \(\frac n4\),那么只有 \(\frac{1}{64}\) 的常数了,总复杂度 \(O(\frac{n^3}{64})\) ,可通过此题。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
std::cin >> n;
std::vector a(n + 1, std::vector<int>(n + 1));
for (int i = 1; i <= n; i += 1) {
for (int j = i; j <= n; j += 1) {
std::cin >> a[i][j];
a[j][i] = a[i][j];
}
}
auto check = [&](int i, int j)->bool{
if (a[i][j] != (i ^ j)) return false;
for (int k = 1; k <= n; k += 1) {
if (k == i || k == j) continue;
int res = (a[i][k] ^ a[k][j] ^ a[i][j]);
if (res != i && res != j) return false;
}
return true;
};
for (int i = 1; i <= n; i += 1) {
for (int j = i + 1; j <= n; j += 1) {
if (check(i, j)) {
std::cout << i << " " << j << "\n";
}
}
}
return 0;
}
J. January's Color
树上前缀和,\(lca\)。
因为最后只能保留 \(y\),并且删掉点的方法是选择同一父亲的两个儿子结点删掉来换它们的父亲,所以只有当 \(y\) 是 \(x\) 的祖先时才可以得到,否则不行。
考虑得到一个点的代价,可以直接买,也可以买它的两个儿子来换它,所以可以先一遍树上 \(dp\) 求出每个点的最小代价,然后设 \(pre_u\) 表示从 \(u\) 结点变到 \(1\) 的最小代价,当 \(y\) 是 \(x\) 的祖先时,答案即 \(pre_x-pre_y\)。
L. Let's Make a Convex!
双指针。
排序后从大到小枚举,判断 \(a_i\) 能否加入 \(l\) 条边的多边形即可,\(l\) 可用指针维护。
M. Mystique as Iris
计数,\(dp\)。
开始想的是只要存在一个数小于 \(n\),那么就一定能变成空数组,后来发现全 \(1\) 时且是奇数个不行,但是只要保证这个数大于 \(1\) 还是可行,于是可以特判掉这种情况(
除去奇数全 \(1\) 的情况下,发现 \(1\) 在位置 \(1\) 和 \(n\) 时也一定可行,因为 \(1\) 的作用就是删掉某一边的数,所以只要另外一边能合成一个数即可,于是只要有连续的两个 \(1\) 也是可行的;考虑用 \(dp\) 找出不合法的情况,设 \(dp_{i,0/1}\) 表示第 \(i\) 个位置放 \(n\sim m\) 还是放 \(1\) 满足不存在 \(1\) 相邻的方案数,那么有转移 \(dp_{i,1}\leftarrow dp_{i-1,0}\),\(dp_{i,0}\leftarrow dp_{i,0}+dp_{i,1}\),最后答案就是 \(m^{cnt}-dp_{n,0}-mask\),其中 \(cnt\) 代表 \(-1\) 的个数,\(mask\) 代表是否能构成奇数全 \(1\) 的情况。
点击查看代码
#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#include <bits/stdc++.h>
#define int long long
#define PII pair<int,int>
#define PIII pair<PII,int>
using namespace std;
//#define endl '\n'
const int N = 2e6 + 10, mod = 1e9 + 7;
int top;
int n, m, k;
string s;
string str = "CWP";
int a[N];
int f[2][N];
int qpow(int x,int n){
int ans=1;
while(n){
if(n&1){
ans*=x;
ans%=mod;
}
x*=x;
x%=mod;
n>>=1;
}
return ans;
}
void solve() {
cin >> n >> m;
int flag=0;
int s0=0;
int f1=1;
for(int i=1;i<=n;i++){
cin>>a[i];
if(a[i]>1&&a[i]<n){
flag=1;
}
if(a[i]!=-1&&a[i]!=1){
f1=0;
}
s0+=a[i]==-1;
}
if(n%2==0)f1=0;
if(flag){
cout<<qpow(m,s0)<<endl;
return;
}
int p=max(0ll,m-n+1);
f[1][0]=1;
for(int i=1;i<=n;i++){
if(a[i]==-1){
f[1][i]+=f[0][i-1];
f[0][i]+=(f[0][i-1]+f[1][i-1])*p%mod;
}else{
if(a[i]==1){
f[1][i]+=f[0][i-1];
}else{
f[0][i]+=(f[0][i-1]+f[1][i-1])%mod;
}
}
f[1][i]%=mod;
f[0][i]%=mod;
}
cout<<(qpow(m,s0)-f[0][n]+mod+mod-f1)%mod<<endl;
}
signed main() {
// freopen("in.txt", "r", stdin);
ios::sync_with_stdio(false);
cin.tie(0);
int t = 1;
// cin >> t;
while (t--) {
solve();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号