2023 CCPC Final G

G. China Convex Polygon Contest

反悔贪心。

首先可以考虑对 \(b\) 排序，显然思考越快的题可以使手里攒着的题更多更有选择的空间。

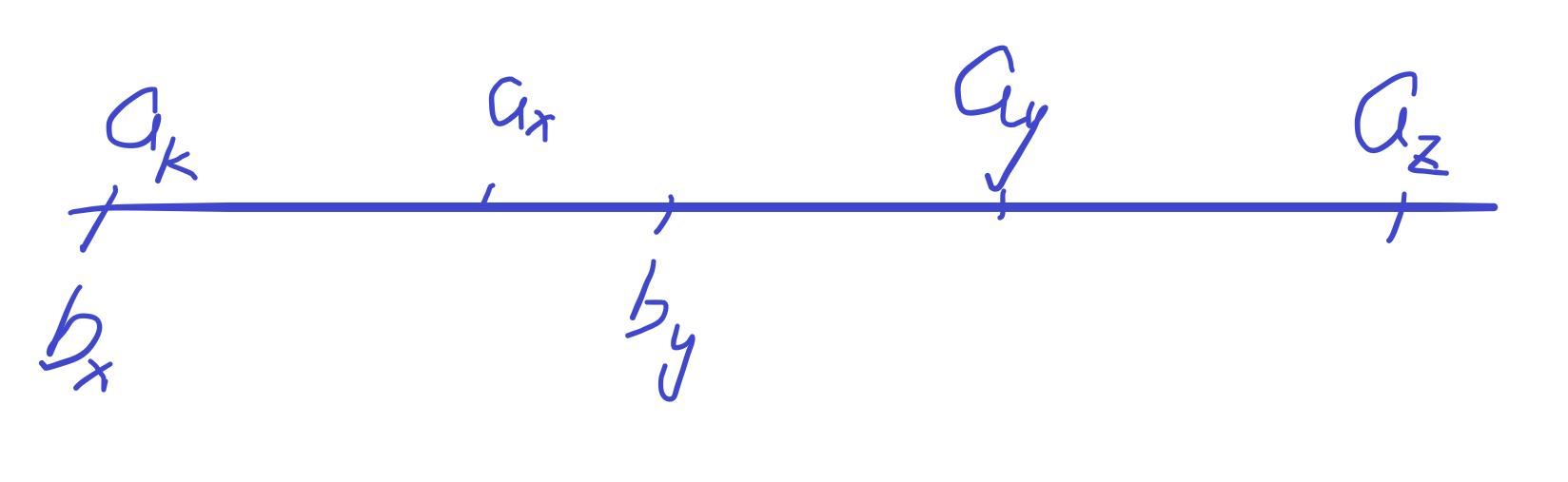
如果正着贪心的话就是，当前能做就立马提交，如果当前的时间更优但选不了就从之前丢一个小的然后选择当前；但是会存在这样一个情况，刚开始把 \(a_x-a_k\) 丢进堆，然后到了 \(b_y\)，如果 \(a_y-b_y \ge a_z-a_y\)，自然选当前段更好，但是反之 \(a_z-a_y>a_y-a_x>a_x-a_k\)，我们就要抛弃掉之前的 \(a_x-a_k\)，让 \(b_x\) 去选 \(a_y-a_x\) 段，\(b_y\) 去选 \(a_z-a_y\)。

因为你不知道 \(b_y\) 是否会在后面更优，于是对于 \(b_y-a_x\) 这一段你就得考虑怎样去维护，由于你的堆里维护的是你选了的，所以你不能直接丢进去，发现这个东西不好维护。

正难则反，考虑反着遍历。

维护一个最大堆，维护你没有选过的答案，枚举到当前 \(a_i\) 时，假设这一段区间内有 \(x\) 个 \(b_j\)，除去最后一个需要特殊处理一下，那么前 \(x-1\) 个显然是选择堆顶的 \(x-1\) 个贡献，这些答案显然是确定的且更优，最后可能会剩一些没用完的 \(b\)，但是后面已经没有贡献了，我们只考虑最接近 \(a_i\) 的那个 \(b\)，以 \(a_x\) 和 \(b_y\) 为例，如果目前堆中仍有答案且比 \(a_y-b_y\) 更优，那么显然，我们这个 \(b_y\) 选后面的更优，这一段直接就放 \(a_y-a_x\) 进去让更前面的选；否则就选上当前的 \(a_y-b_y\)，然后把 \(b_y-a_x\) 加到堆顶（记为 \(S\rightarrow S+b_y-a_x\) ），如果你后续有 \(b\) 选到了这个堆顶，意味着，是之前那个 \(b\) 反悔了选了 \(S\)，而现在这个 \(b\) 选了 \(a_y-a_x\)，但是总的贡献仍然有 \(S + a_y - a_x\)。

点击查看代码

#include <bits/stdc++.h>

using i64 = long long;

void solve() {

	int n, m;
	std::cin >> n >> m;

	std::vector<int> a(n + 2);
	std::vector<i64> b(n);
	for(int i = 1; i <= n; i += 1) {
		std::cin >> a[i];
	}
	a[n + 1] = m;
	for(int i = 0; i < n; i += 1) {
		std::cin >> b[i];
	}

	sort(b.begin(), b.end());
	for(int i = 1; i < n; i += 1) {
		b[i] += b[i - 1];
	}

	while(b.size() && b.back() > m) {
		b.pop_back();
	}

	int ans = 0;

	std::priority_queue<int> pq;
	for(int i = n; i >= 0; i -= 1) {
		std::vector<int> vec;
		while(b.size() && b.back() >= a[i]) {
			vec.push_back(b.back());
			b.pop_back();
		}

		std::reverse(vec.begin(), vec.end());
		while(vec.size() > 1 && pq.size()) {
			ans += pq.top();
			pq.pop();
			vec.pop_back();
		}

		if(vec.size()) {
			int x = a[i + 1] - vec[0];
			int y = 0;
			if(pq.size()) {
				y = pq.top();
				pq.pop();
			}

			if(y >= x) {
				ans += y;
				pq.push(a[i + 1] - a[i]);
			} else {
				ans += x;
				y += vec[0] - a[i];
				pq.push(y);
			}
		} else {
			pq.push(a[i + 1] - a[i]);
		}
	}

	std::cout << ans << "\n";

}
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);

	int t;
	std::cin >> t;
	while (t--) {
		solve();
	}

	return 0;
}