Codeforces Round 1053 (Div. 2) A~E
A. Incremental Subarray
思维,观察。
把它那个数字表打出来观察,会发现如果给的 \(a\) 不是一段连续的区间,只会出现一次;否则看 \(a_m\),那么答案就是 \(\sum_{i=1}^n[i\ge a_m]=n-a_m+1\)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
void solve() {
int n, m;
cin >> n >> m;
vector<int> a(m);
for (auto &i : a) {
cin >> i;
}
bool f = 1;
for (int i = 1; i < m; i += 1) {
if (a[i] != a[i - 1] + 1) {
f = 0;
break;
}
}
if (!f) {
cout << 1 << "\n";
}
else {
int x = a[m - 1];
cout << n - x + 1 << "\n";
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while (t--) {
solve();
}
return 0;
}
B - Incremental Path
打表,模拟。
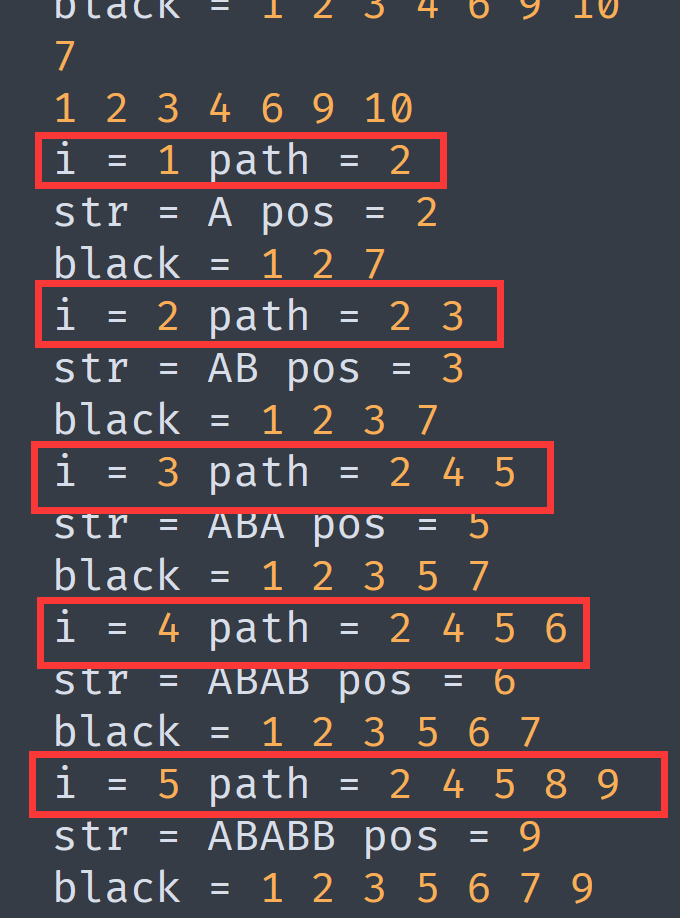
把从 \(1\sim i\) 每个人的路径打印出来观察,会发现第 \(i\) 个人的路径线路就是 \(i - 1\) 个人的线路去掉最后一个点然后再更新两步即可,这之前的路线和 \(i - 1\) 的重合。
所以我们只要维护每个人的最后两步就行,我这里是用了 \(\text{vector}\) 去维护了,然后再更新 \(s_{i-1}\) 和 \(s_i\) 两步就是第 \(i\) 个人的最终停止点,找下一个白色块的时候可以直接 \(\text{set}\) 暴力即可,因为线路是单调递增的,每个点最多只会遍历两次。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
void solve() {
int n, m;
cin >> n >> m;
string s;
cin >> s;
s = " " + s;
vector<int> a(m + 1);
set<int> black;
for (int i = 1; i <= m; i += 1) {
cin >> a[i];
black.insert(a[i]);
}
vector<int> lst;
lst.push_back(1);
for (int i = 1; i <= n; i += 1) {
if (lst.back() != 1) {
lst.pop_back();
}
int pos = lst.back();
if (i - 1 >= 1) {
pos += 1;
if (s[i - 1] == 'B') {
while (black.count(pos)) {
pos += 1;
}
}
lst.push_back(pos);
}
pos += 1;
if (s[i] == 'B') {
while (black.count(pos)) {
pos += 1;
}
}
lst.push_back(pos);
black.insert(pos);
}
cout << black.size() << "\n";
for (auto &x : black) {
cout << x << " ";
}
cout << "\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while (t--) {
solve();
}
return 0;
}
C. Incremental Stay
贪心。
对于一个固定的 \(k\),那么我们只要保证始终有 \(k-1\) 个人待着博物馆,其他时候,有一个退出,就有一个人进入,这样贪心是最优的,能最大限度保证博物馆任何时间的人数都是最多的。
那么存在这样一种贪心策略,我先放 \(k - 1\) 进入,那么剩下一个人就是进去退出进去退出如此循环,最后 \(k-1\) 个人依次退出。
那么前 \(k - 1\) 个人的贡献就是 \(a_{2n}-a_1+a_{2n-1}-a_2+...+a_{2n-k+2}-a_{k-1}\),中间的就是 \(a_{k+1}-a_k+a_{k+3}-a_{k+2}+...\),中间的部分其实就是奇偶下标的和相减,前面 \(k - 1\) 人的答案是累计的,可以在从 \(k\rightarrow k+1\) 时 \(O(1)\) 转移。

点击查看代码
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
void solve() {
int n;
cin >> n;
i64 even = 0, odd = 0;
vector<int> a(2 * n + 1);
for (int i = 1; i <= 2 * n; i += 1) {
cin >> a[i];
if (i & 1) {
odd += a[i];
}
else {
even += a[i];
}
}
i64 sum = 0;
int l = 1, r = 2 * n;
for (int k = 1; k <= n; k += 1) {
cout << sum + even - odd << " \n"[k == n];
sum += a[r] - a[l];
if (r % 2 == 0) {
even -= a[r], odd -= a[l];
}
else {
odd -= a[l], even -= a[r];
}
swap(odd, even);
r -= 1, l += 1;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while (t--) {
solve();
}
return 0;
}
D - Grid Counting
组合数学。
首先忽略第一个条件,看二三条件[1]。
\((1,1)\) 一定是黑色的,因为只有此时满足第二个条件使得 \(k=1\),且此时满足第三个条件使得 \(k=n\),所以对于所有的 \(i\ge 2\),\((i,1)\)都不能选,它们会在第三个条件得到 \(k=n\) 和 \((1,1)\) 冲突。
\((1,2)\) 或者 \((2,2)\) 是黑色的,它们在第二个条件使得 \(k=2\),此时满足第三条件使得 \(k=n-1\),所以对于所有的 \(i\ge 3\),\((i,2)\)都不能选,它们会在第三个条件得到 \(k=n - 1\) 和前面冲突。
以此类推,从 \((1,1\sim n)\) 开始重复同样的过程,可以得到只有 \((i,j)\) 和 \(i \le n -j + 1\) 可以是黑色的。
因此,对于每列来说,只能恰好有一个黑色格子 \((i,j)\) ,且 \(i \le \min(j, n -j + 1)\),所以需要满足 \(\sum_{i=1}^na_i = n\)。
从前往后可选择的位置是递减的,但前面选择的位置后面不一定合法,需要从后往前遍历行,每一行有当前可选择的列记为 \(\text{has}\),填充当前合法的 \(a_i\) 列,共有 \(\binom{has}{a_i}\),填完后把这 \(a_i\) 列减去即可。
对于可选择列,满足 \((i,j)\) 和 \(i \le n -j + 1\) 的要求就是从后往前每次都多两个位置可选,奇数行会在中间行多一个。
代码中 Z 类型为取模类。
点击查看代码
using Z = ModInt<MOD[0]>;
//----计算组合数----//
struct Comb {
int n;
std::vector<Z> _fac; //阶乘
std::vector<Z> _invfac; //阶乘的逆元
std::vector<Z> _inv; //数字的逆元
Comb() : n{0}, _fac{1}, _invfac{1}, _inv{0} {}
Comb(int n) : Comb() {
init(n);
}
void init(int m) {
if (m <= n) {
return;
}
_fac.resize(m + 1);
_invfac.resize(m + 1);
_inv.resize(m + 1);
for (int i = n + 1; i <= m; i++) {
_fac[i] = _fac[i - 1] * i;
}
_invfac[m] = _fac[m].inv();
for (int i = m; i > n; i--) {
_invfac[i - 1] = _invfac[i] * i;
_inv[i] = _invfac[i] * _fac[i - 1];
}
n = m;
}
Z fac(int m) {
if (m > n) {
init(2 * m);
}
return _fac[m];
}
Z invfac(int m) {
if (m > n) {
init(2 * m);
}
return _invfac[m];
}
Z inv(int m) {
if (m > n) {
init(2 * m);
}
return _inv[m];
}
Z C(int n, int m) {
if (n < m || m < 0) {
return 0;
}
return fac(n) * invfac(m) * invfac(n - m);
}
Z A(int n, int m) {
if (n < m || m < 0 ) {
return 0;
}
return fac(n) * invfac(n - m);
}
} comb;
//----计算组合数----//
void solve() {
int n;
cin >> n;
vector<int> a(n + 1);
for (int i = 1; i <= n; i += 1) {
cin >> a[i];
}
int has = 0;
Z ans = 1;
for (int i = n; i >= 1; i -= 1) {
if (2 * i == n + 1) {
has += 1;
}
else if (2 * i <= n) {
has += 2;
}
if (has < a[i]) {
cout << 0 << "\n";
return;
}
ans *= comb.C(has, a[i]);
has -= a[i];
}
if (has) {
ans = 0;
}
cout << ans << "\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while (t--) {
solve();
}
return 0;
}
E - Limited Edition Shop
数据结构优化dp。
考虑朴素 \(dp\) [2],设 \(dp_{i,j}\) 表示 Alice 买了前 \(i\) 个物品,Bob 买了前 \(j\) 个物品的物品的价值的最大总和,那么 Bob 买了前 \(j - 1\) 个有转移 \(dp_{i,j}=dp_{i,j-1}\);如果第 \(i\) 个物品不在 Bob 的前 \(j\) 个内,有转移 \(dp_{i,j}=\max(dp_{i,j},dp_{i-1,j}+v_i)\),否则 \(dp_{i,j}=\max(dp_{i,j},dp_{i-1,j})\),最后的答案就是 \(\max_{j=0}^ndp_{n,j}\) 。
这样复杂度是 \(O(n^2)\) 的,需要优化。
假设[1:1] Alice 选取的某个子集 \(S\),那么对于所有的 \(x\notin S, y\in S\),如果在 \(a\) 中有 \(posa_x < posa_y\),在 \(b\) 中也要有 \(posb_x < posb_y\)。证明也好证,如果 \(posb_x > posb_y\),那么因为 \(posa_x < posa_y\),所以 Alice 要等 Bob 选完 \(x\) 才能选 \(y\),但是 \(posb_y < posb_x\),所以 Bob 要选 \(x\) 的话就一定要把 \(y\) 先选了。
记 \(pos_x\) 为 \(a\) 中 \(x\) 的值在 \(b\) 中的位置,也就是说对于 \(a_i\) 来说,\([0, pos_{a_i}-1]\) 对应的值都可以选择或不选择 \(a_i\),如果不选择 \(a_i\),就类似 \(dp_{i,pos_{a_i}}=\max_{j=0}^{pos_{a_i}-1}dp_{i-1,j}\),否则 \(dp_{i,pos_{a_i}}=\max_{j=0}^{pos_{a_i}-1}dp_{i-1,j}+v_{a_i}\)
考虑用线段树来维护第二维,每层的转移就把第一维滚动掉了,只需要计算 \([0,pos_{a_i}-1]\) 和对其区间加上 \(v_{a_i}\) 后两个区间最大值赋值给 \(pos_{a_i}\) 即可。
因为 \(j\) 可以为 \(0\),所以我这线段树都整体偏移了一位。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
template<class Node>
struct SegmentTree {
#define lc u<<1
#define rc u<<1|1
const int n, N;
vector<Node> tr;
SegmentTree(): n(0) {}
SegmentTree(int n_): n(n_), N(n * 4 + 10) {
tr.reserve(N);
tr.resize(N);
}
SegmentTree(vector<int> init) : SegmentTree(init.size() - 1) {
function<void(int, int, int)> build = [&](int u, int l, int r) {
tr[u].l = l, tr[u].r = r;
init_lazy(tr[u]);
if (l == r) {
tr[u] = {l, r, 0, init[l]};
return ;
}
i64 mid = (l + r) >> 1;
build(lc, l, mid);
build(rc, mid + 1, r);
pushup(tr[u], tr[lc], tr[rc]);
};
build(1, 1, n);
}
void cal_lazy(Node & fa, Node & ch) {
i64 b = fa.add;
ch.Max += b;
}
void tag_union(Node& fa, Node& ch) {
i64 b = fa.add;
ch.add += b;
}
void init_lazy(Node& u) {
u.add = 0;
}
void pushdown(i64 u) {
if (tr[u].add != 0) {
cal_lazy(tr[u], tr[lc]);
cal_lazy(tr[u], tr[rc]);
tag_union(tr[u], tr[lc]);
tag_union(tr[u], tr[rc]);
init_lazy(tr[u]);
}
}
void pushup(Node& U, Node& L, Node& R) { //上传
U.l = L.l,U.r = R.r;
U.Max = max(L.Max, R.Max);
}
void modify(int u, int l, int r, int k) {
if (tr[u].l >= l && tr[u].r <= r) {
tr[u].add += k;
tr[u].Max += k;
return ;
}
pushdown(u);
int mid = (tr[u].l + tr[u].r) >> 1;
if (l <= mid) {
modify(lc, l, r, k);
}
if (r > mid) {
modify(rc, l, r, k);
}
pushup(tr[u], tr[lc], tr[rc]);
}
void modify(int u, int pos, i64 k) {
if (tr[u].l >= pos && tr[u].r <= pos) {
tr[u].Max = k;
return ;
}
pushdown(u);
int mid = (tr[u].l + tr[u].r) >> 1;
if (pos <= mid) {
modify(lc, pos, k);
}
if (pos > mid) {
modify(rc, pos, k);
}
pushup(tr[u], tr[lc], tr[rc]);
}
Node query(int u, int l, int r) { //区查
if (l <= tr[u].l && tr[u].r <= r) {
return tr[u];
}
int mid = tr[u].l + tr[u].r >> 1;
pushdown(u);
if (r <= mid) {
return query(lc, l, r);
}
if (l > mid) {
return query(rc, l, r);
}
Node U;
Node L = query(lc, l, r), R = query(rc, l, r);
pushup(U, L, R);
return U;
}
};
struct Node { //线段树定义
int l, r;
i64 Max, add;
};
void solve() {
int n;
cin >> n;
vector<int> v(n + 1), a(n + 1), b(n + 1), pos(n + 1);
for (int i = 1; i <= n; i += 1) {
cin >> v[i];
}
for (int i = 1; i <= n; i += 1) {
cin >> a[i];
}
for (int i = 1; i <= n; i += 1) {
cin >> b[i];
pos[b[i]] = i + 1;
}
vector<int> init(n + 2);
SegmentTree<Node> S(init);
for (int i = 1; i <= n; i += 1) {
i64 val = S.query(1, 1, pos[a[i]]).Max;
S.modify(1, 1, pos[a[i]] - 1, v[a[i]]);
val = max(val, S.query(1, 1, pos[a[i]]).Max);
S.modify(1, pos[a[i]], val);
}
cout << S.query(1, 1, n + 1).Max << "\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while (t--) {
solve();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号